Любую ферму можно рассматривать как балку перекрытия, только не сплошную, а сквозную. Как и балки сплошного сечения, изготовленные из древесины, металла, железобетона, другого материала, фермы используются для перекрытия различных пролетов. Но в отличие от балок сплошного сечения, в фермах прочностные свойства материала, из которого изготовлена ферма, используются максимально. Например:
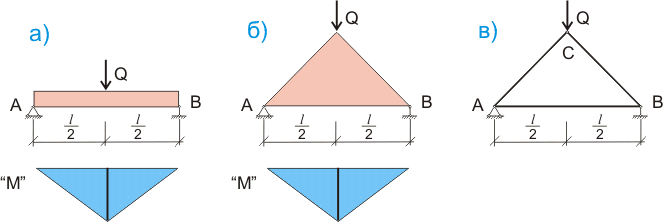
Рисунок 1.
Когда мы рассчитываем параметры поперечного сечения балки, за основу мы берем максимальный изгибающий момент. В итоге материал балки постоянного сечения, показанной на рисунке 1.а, будет использован, условно говоря, на 25%, так как максимальный изгибающий момент действует только в одном сечении посредине балки, а на опорах он равен нулю. Если мы изготовим балку переменного сечения, как показано на рисунке 1.б, то материал такой балки будет использован, условно говоря, на 50%, так как нормальные сжимающие и растягивающие напряжения распределяются по всему сечению балки и максимальных значений достигают вверху и внизу балки. А если мы изготовим некую конструкцию, показанную на рисунке 1.в, то на стержни такой конструкции вообще не будет действовать изгибающий момент (конечно, при условии, что нагрузка будет приложена так, как показано на рисунке 1.в). В стержнях АС и ВС будут действовать сжимающие напряжения, а в стержне АВ - растягивающие.
Конструкция, показанная на рисунке 1.в, является простейшим видом фермы.
Ферма - это стержневая система, которая останется геометрически неизменяемой после условной замены ее жестких узлов шарнирными
Конечно же в абсолютном большинстве случаев фермы изготавливаются с достаточно жесткими узлами, специальных шарнирных соединений никто не делает, а
условная замена жестких узлов шарнирными нужна для максимального упрощения расчета
Так ферма, показанная на рисунке 1.в, является статически определимой системой, т.е. определить нормальные напряжения в стержнях такой фермы мы можем, используя стандартный набор из трех уравнений равновесия. А если бы узлы фермы были жесткими, то такая ферма была бы трижды статически неопределимой со всеми вытекающими отсюда последствиями. Как показывает практика, результаты расчетов параметров фермы при условной замене жестких узлов шарнирными достаточно близки к результатам для фермы с жесткими узлами при соотношении длины стержня к его высоте или ширине l/h > 10 и при приложении нагрузки в узлах фермы. А чтобы такие расчеты можно было смело производить, конструкция должна быть геометрически неизменяемой.
Наглядно представить, что такое
геометрическая неизменяемость
лучше всего поможет обычный детский конструктор из стальных шариков и разноцветных стерженьков с магнитами - магнитная мозаика:

Фотография 1. Магнитная мозаика.
Из деталей такого конструктора можно собирать достаточно сложные объемные конструкции, намного сложнее чем, та что показана на фотографии 1. Однако пока объемные конструкции нас не интересуют, поэтому оставим их создание и исследование детям, а сами рассмотрим две плоские конструкции:
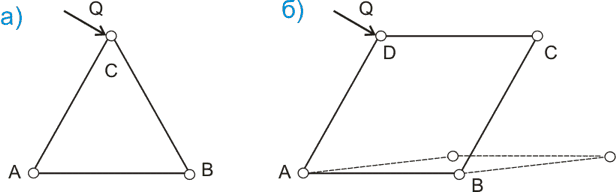
Рисунок 217.2.
Если мы соберем из трех стержней и трех шариков конструкцию, похожую на нашу ферму (рисунок 2.а), то как бы мы ни прикладывали нагрузку Q к узлу С (разумеется в плоскости конструкции и при этом узлы А и В будут иметь какую-то опору, например, стол), то конструкция будет сохранять свою геометрическую форму треугольника до тех пор, пока сила, приложенная к узлу С не превысит силу сцепления магнита и шарика. Если мы добавим к этой конструкции еще один стержень и еще один шарик так, как показано на рисунке 2.б, то такая конструкция будет очень неустойчивой и если сразу не сложится под действием силы тяжести, то даже при незначительном воздействии некоторой силы Q все равно сложится, т.е. изменит свою геометрическую форму. Чтобы сделать конструкцию, показанную на рисунке 2.б, геометрически неизменяемой, достаточно добавить всего лишь один стержень между узлами D и В. Если добавлять к конструкции на рисунке 2.а по два стержня и одному шарику так, чтобы получался новый треугольник, то мы таким образом можем получить достаточно длинную, геометрически неизменяемую и статически определимую ферму. Вообще вариантов компоновки стержней может быть много, некоторые из этих вариантов рассматриваются ниже.
Само собой кроме плоских ферм, у которых оси всех стержней расположены в одной плоскости, как в вышерассмотренных случаях, в строительстве применяются пространственные фермы, оси элементов которых не лежат в одной плоскости, как на фотографии 1. Расчет пространственных ферм часто удается свести к расчету нескольких плоских ферм. Впрочем, расчет как пространственных, так и плоских ферм не является темой данной статьи.
Расстояние между осями опор фермы l называется пролетом. Стержни, расположенные по внешнему контуру фермы называются поясными и образуют верхний сжимаемый и нижний растягиваемый пояс фермы. Стержни АС и ВС на рисунке 1.в образуют верхний пояс, стержень АВ - нижний пояс. Стержни, соединяющие верхний и нижний пояс, образуют решетку фермы. Вертикальные стержни, на которые действуют сжимающие напряжения, называются стойками, наклонные стержни называются раскосами. Расстояние между соседними узлами любого пояса фермы обычно измеряется по горизонтали и называется панелью.
Классифицировать фермы можно по следующим 5 признакам:
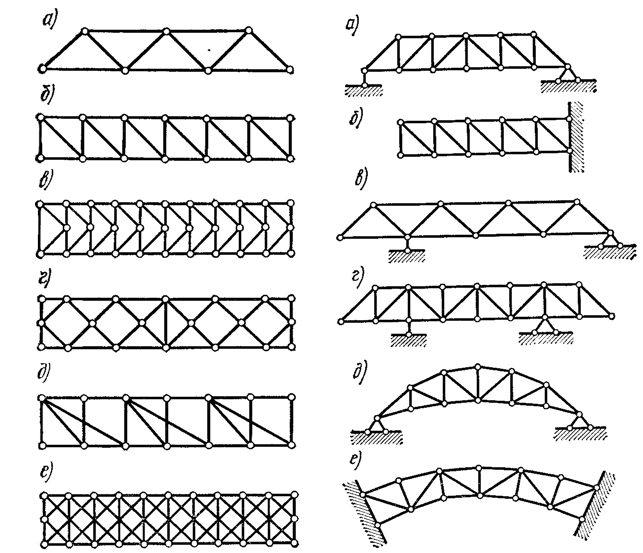
Рисунок 3. Рисунок 4.
1. Характер очертания внешнего контура
Фермы бывают с параллельными поясами (рис. 3), с ломаным или так называемым полигональным расположением поясов. К последним относятся, например, фермы с параболическим очертанием верхнего пояса (рис. 4.д) и фермы треугольного очертания (рис.1.в).
2. Тип решетки
По этому признаку фермы делятся на фермы с треугольной решеткой (рис. 3.а), фермы с раскосной решеткой (рис. 3.б), фермы с полураскосной решеткой (рис. 3.в), фермы с ромбической решеткой (рис 3.г), двухрешетчатые (рис. 3.д), многорешетчатые рис. 3.е).
3. По типу опирания
фермы могут быть закрепленными у обоих концов - балочными (рис. 4.а) или арочными (рис. 4.д, е), консольными - закрепленными у одного конца (рис. 4.б), балочно консольными (рис. 4.в, г)
4. Назначение фермы
В зависимости от назначения различают фермы стропильные, крановые, башенные, мостовые и другие.
5. Уровень езды
Мостовые фермы в зависимости от уровня езды делятся на фермы с ездой понизу, фермы с ездой поверху и фермы с ездой посередине.
Далее нас, как строителей и проектировщиков довольно мелкого масштаба будут интересовать только стропильные фермы. Основные принципы расчета ферм не так сложны, как может показаться на первый взгляд. |

