
Рисунок 227.1 . Расчетные схемы стропил.
На рисунке 227.1.3 (номер 3 выделен коричневым цветом) представлена стропильная система, которую можно рассматривать как треугольную арку с затяжкой или как ферму из трех стержней. Если соединения в ключе арки и на опорах не обеспечивают должной жесткости, то такую арку можно рассматривать как трехшарнирную - с замком и шарнирными опорами на пятах арки. Такое допущение делает рассматриваемую арку статически определимой и значит расчет такой арки не представляет больших проблем. Ну а если не учитывать свес стропильных ног за поверхность стены, особенно если этот свес образован кобылками, как на рисунке 227.1.1 б), то такую стропильную систему можно рассматривать как бесконсольную и это еще более упрощает расчет
Для определения нормальных и касательных напряжений в стержнях арки - стропильных ногах и затяжке используются такие же уравнения статического равновесия, как и для обычной балки. Но чтобы не погрузиться по самые помидоры в абстрактные формулы расчета, добавим сюда вполне вероятную жизненную ситуацию:
Строится двухэтажный дом в Московской области, высота стен h = 6 м, расстояние в свету между стенами - пролет арки - b = 6 м, кровля - волнистые асбестоцементные листы, уклон кровли α = 30о, при таком уклоне длина стропильных ног будет составлять l = 3.464 м, стрела арки f = 1.732 м (проблемы определения сторон треугольника - длины стропильной ноги и стрелы арки - здесь и далее не рассматриваются), шаг стропильных ног - 1 м, обрешетка из необрезных досок толщиной 25 мм. Чердачное помещение - нежилое. Предварительно принятое сечение стропил -50х150 мм. Требуется подобрать сечение затяжки и определить, достаточно ли будет такого сечения стропильных ног.
Как определить нагрузки на стропила, рассказывается отдельно, здесь же мы просто отметим, что снег - материя очень не постоянная, он может лежать равномерно на крыше, а может переноситься ветром с одного ската на другой. Поэтому для расчетов более правильно будет принять наиболее неблагоприятное сочетание нагрузок, когда на одном скате снега больше и тогда расчетная распределенная нагрузка будет составлять qлев = 326.1 кг/м, а на втором скате снега меньше и расчетная нагрузка на вторую часть арки будет составлять:
qпр = qcт + qo + qш +qs = 3.75 + (6.25 + 16.77 + 180х0.75х1.2)1.1 = 207.3 кг/м
Так как при уклоне кровли 30о над кровлей при воздействии ветровых нагрузок будет создаваться разрежение (при h/b = 1), то влияние горизонтальной и вертикальной составляющей ветровой нагрузки для упрощения расчетов учитывать не будем, небольшой запас по прочности не помешает, а расчеты при этом упростятся. Теперь пришло время использовать уравнения статического равновесия. Если Ньютон прав и удар падающего яблока только усилил умственные способности Ньютона, приведшие в частности к формулировке 3 законов, то мы можем заменить опоры арки силами. При этом из условий статического равновесия следует, что сумма всех сил, действующих вдоль оси х и сумма всех сил действующих вдоль оси у равны 0. Вертикальные силы называются вертикальными реакциями опор и как правило обозначаются литерами V (от англ. vertical), а горизонтальные силы - горизонтальными реакциями опор H (от англ. horizontal). В данном случае роль горизонтальных опор выполняет затяжка, значит, горизонтальные опорные реакции - это и будет нагрузка, действующая на затяжку.
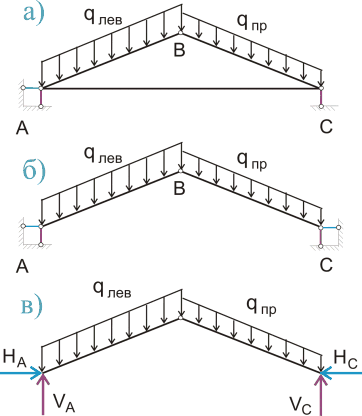
Рисунок 268.1. Расчетная схема треугольной трехшарнирной арки с затяжкой на опорах
В математическом выражении это выглядит так:
∑Qу = - qлевl - qпрl + Vлев + Vпр = 0 (268.1.1) - для сил, действующих вдоль оси у.
∑Qх = НА - НС = 0 (268.1.2) - для сил, действующих вдоль оси х.
Из уравнения (1.2) следует, что:
НА = НС (268.1.3)
Примечание: Знак, с которым значение силы подставляется в уравнения, зависит от направления действия силы. Некоторые считают, что если сила направлена вниз, то она считается положительной, а если вверх, то отрицательной. Мне больше по духу иной взгляд, основанный на древнейших общечеловеческих традициях. Поэтому в данном примере положительной считается вертикальная сила, направленная вверх (в небо, в рай), так направлена ось у декартовой системы координат, а отрицательной - сила, направленная вниз (в землю, в ад). Для сил, действующих в горизонтальном направлении, положительной считается сила, направленная слева направо (мы так читаем и пишем, впрочем к представителям азиатских культур это не относится), так направлена ось х декартовой системы координат, а отрицательной - сила, направленная справа налево. Если действие момента относительно рассматриваемой точки направлено по часовой стрелке, то такой момент считается положительным, если против часовой стрелки, то отрицательным. Впрочем принципиального значения это не имеет.
Если бы на оба ската кровли действовала одинаковая нагрузка, то определить вертикальные опорные реакции было бы совсем просто, при qлев = qпр, Vлев = Vпр = qпрb/2 = qлевb/2. Однако в данном случае нагрузка неравномерная и потому придется воспользоваться еще одним из уравнений статического равновесия, а именно уравнением моментов в точке, расположенной на одной из опор, например, уравнение моментов относительно точки, расположенной на опоре А, будет иметь вид:
∑МА = qлевb2/8 + qпр(b/2 + b/4)b/2 - VСb = 0 (268.1.4)
откуда следует, что
VС = qлевb/8 + 3qпрb/8 = (326.1 + 3·207.3)6/8 = 711 кг
тогда значение вертикальной реакции на левой опоре согласно уравнения (268.1.1) составит:
VА = (qлев + qпр)b/2 - VС = (326.1 + 207.3)3 - 711 = 889.2 кг
Примечание: В данном случае нас интересует нагрузка относительно оси х, поэтому в расчетах используется не длина стропил l, а длина проекции стропил на ось х, равная b/2. Впрочем, насколько справедливо данное предположение, мы проверим чуть позже.
Площадь опирания стропильной ноги на мауэрлат должна составлять не менее:
F = VA/Rсм = 889.2/30 = 29.63 ≈ 30 см2.
Где Rсм - расчетное сопротивление смятию древесины поперек волокон.
Ну а теперь самое время определить значение горизонтальных опорных реакций. Когда мы составляли уравнение моментов относительно точки, расположенной на опоре А, то моменты от действия горизонтальных опорных реакций не учитывали. И это логично, так как опорные реакции направлены по оси х и потому плечо силы (в данном случае горизонтальных опорных реакций) равно нулю, следовательно и момент от таких сил равен нулю. Для того, чтобы в уравнение моментов можно было подставить моменты от горизонтальных опорных реакций, нам нужно найти такую точку, в которой значение изгибающего момента равно нулю и при этом точка не находится на оси х. И такая точка есть - это замок арки - тот самый третий шарнир, наличие которого превращает арку в статически определимую, потому как на шарнирной опоре или в месте шарнирного соединения между конструкциями значение изгибающего момента всегда равно нулю (конечно при условии, что на шарнирной опоре не приложен изгибающий момент). Таким образом, зная стрелу арки f (в данном случае она составляет 1.732 м), мы достаточно легко можем определить значение горизонтальных опорных реакций:
∑МВлев = - qлевb2/8 + VАb/2 - НАf = ∑МВпр = qпрl·b/4 - VСb/2 + НСf = 0 (268.1.6)
Таким образом для определения горизонтальной опорной реакции достаточно решить одно из уравнений, вытекающих из формулы (268.1.6):
НС= (- qпрb2/8 + VСb/2)/f = (-207.3·62/8 + 711·6/2)/1.732 = 692.927 кг
Для уверенности в допущенном ранее предположении, да и вообще для проверки правильности произведенных расчетов проверим значение горизонтальной опорной реакции на левой опоре:
НА= (- qлевb2/8 + VАb/2)/f = (-326.1·62/8 + 889.2·6/2)/1.732 = 692.927 кг
Тут может возникнуть следующий вопрос: если на затяжку с двух сторон действуют опорные реакции, то продольная растягивающая сила, действующая на затяжку, будет больше и составит:
Nзат = 2НА = 2НС = 2·693 = 1386 кг?
Однако уравнения статического равновесия показывают, что это не так. Тем не менее даже если вести расчет по в 2 раза завышенному значению, то для затяжки, изготавливаемой из сосны первого сорта, расчетное сопротивление растяжению составит Rр = 100 кгс/см2 (10 Мпа). Это значит, что площадь сечения затяжки может составлять:
F = H/Rp = 1386/100 = 13.86 cм2
Так как это достаточно малая площадь сечения, то сечение затяжки можно подбирать, исходя из конструктивных соображений (с учетом максимально допустимой гибкости растягиваемого элемента) или из имеющегося в наличии лесоматериала, а также от конструктивного решения узлов элементов.
Например, в данном случае при расчетной длине затяжки l0 = 580 см (с учетом геометрии стропильной системы) и максимально допустимой гибкости λ = 200. Размеры сторон поперечного сечения затяжки должны быть не менее
h или b ≥ 600/57.5 = 10.1 см (согласно графика 250.2)
И если для высоты h это вполне приемлемое значение с учетом необходимости крепления к стропильной ноге, то для ширины b это достаточно много. Разумным выходом из этой ситуации будет устройство дополнительных горизонтальных связей, перпендикулярных плоскости арки и расположенных посредине затяжки. Для этого достаточно сбить или другим образом скрепить затяжки брусками или досками и если нет возможности упереть эти бруски в фронтальные стены, то сделать несколько подкосов в горизонтальной плоскости. Тогда расчетная длина затяжки уменьшится примерно в 2 раза, соответственно и ширины b = 5 см будет достаточно. Экономия материалов при этом ожидается ощутимая.
Количество гвоздей, для соединения стропил с затяжкой подсчитать также не сложно. Например, если использовать для этого гвозди диаметром 0.5 см, то при несущей способности одного гвоздя 87.5 кг потребуется 693/87.5 = 7.92 точнее 8 гвоздей на каждый стык.
Примечание: если затяжка будет одновременно балкой перекрытия или по затяжке во время монтажа перекрытия будут ходить люди, то тогда затяжку следует рассчитывать отдельно на соответствующие нагрузки.
Осталось проверить, будет ли предварительно выбранное сечение стропил 50х150 мм достаточным для восприятия действующих нагрузок. Для этого нужно определить значение максимального изгибающего момента, действующего на поперечное сечение стропильной ноги и при этом учесть, что на стропильную ногу, в рассматриваемом поперечном сечении будет действовать также сжимающее усилие, а так как стропила являются прямолинейными, то даже при центральном сжатии могут потерять устойчивость. В математическом выражении это будет выглядеть так:
(N/φF) + (Mх/Wz) ≤ Rи (214.3.1)
где N - значение продольной сжимающей нагрузки, возникающей в поперечном сечении стропил, кг;
F - площадь сечения стропильной ноги, площадь предварительно принятого нами сечения составляет F = 5х15 = 75 см2;
φ - коэффициент продольного изгиба, как определить этот коэффициент, рассказывается отдельно. В данном случае значение коэффициента будет составлять φ = 0.47, если обрешетка будет обеспечивать надежное соединение стропильных ног между собой и тогда для определения коэффициента используется не наименьшая сторона (ширина стропила, равная 5 см), а наибольшая (высота стропила, равная 15 см);
Mх - значение изгибающего момента, возникающего в поперечном сечении на расстоянии х от опоры А под действием вертикальных составляющих нагрузки. Вообще-то при конструкции стропильной системы с обрешеткой и настилом, как ни крути, все равно будет эксцентриситет приложения нагрузки, действующей на стропила, но так как эксцентриситет этот будет относительно не большим, то для упрощения расчетов учитывать момент, возникающий при внецентренном приложении нагрузки учитывать не будем, к тому же опорные реакции мы определяли без учета эксцентриситета;
Wz - момент сопротивления поперечного сечения, для предварительно принятого нами сечения момент сопротивления составит Wz = 5х152/6 = 187.5 см3;
Rи - расчетное сопротивление древесины изгибу, сжатию вдоль волокон стропильной ноги растяжению, сжатию и изгибу по пределу текучести, в данном случае Rи = 140 кг/см2 (для сосны 1 сорта).
Таким образом нам не известны только значения продольной нагрузки и значение изгибающего момента. Их мы сейчас и определим.
Примечание: Вообще-то геометрия идеальной арки такова, что значение изгибающего момента во всех поперечных сечениях равно нулю, но это явно не наш случай, для этого стержни арки должны быть как минимум криволинейными, а у нас прямолинейные, да и сжимающая нагрузка должна прикладываться по оси арки. Но в данной ситуации есть и положительное свойство - нам не придется долго вычислять угол наклона поперечного сечения относительно оси х, и соответственно угол действия сил и нагрузок. Так как стержни арки прямолинейные, то этот угол всегда составляет 30о.
На данном этапе для определения поперечного сечения, в котором действуют максимальные напряжения, следует построить эпюры поперечных сил, моментов и продольных сил.
Но так как мы рассматриваем горизонтальную проекцию наклонного стержня арки, то эпюры поперечных сил и изгибающих моментов для такого наклонного стержня не будут ничем отличаться от эпюр для обычной горизонтальной балки. Только добавится продольная сила, причем при выбранной методике расчета, значение ее постоянно во всех поперечных сечениях стержня и составит:
NA-B = HA/cosa = 692.927/0.866 = 800.15 кг
Наиболее нагруженной у нас является левая часть арки, поэтому вполне логично далее рассматривать именно эту часть арки.
Максимальный момент будет в сечении, расположенном посредине наклонной балки - стропильной ноги, там где значение поперечной силы равно нулю и составит:
Мb/4 = qлевb2/32 = 326.1·62/32 = 366.862 кг·м или 36686.2 кг·см (268.1.7)
Мb/4/Wz = 36686.2/187.5 = 195.66 кг/см2 > Rи = 140 кг/см2.
Примечание: тут опять же может возникнуть вопрос, а почему это мы определяем максимальный момент по какой-то левой формуле? Ну то есть как для обычной горизонтальной балки, у которой реакции на опорах равны, а у нас какая-то совсем другая конструкция, при которой вертикальная опорная реакция в точке А явно больше qb/4 и вообще почти равна qb/2, кроме того есть еще горизонтальная опорная реакция, а чему может быть равна вертикальная опорная реакция в точке В - вообще не понятно?
Ответ будет следующим:
Полная формула для расчета момента в точке b/4 (горизонтальная проекция):
Mb/4 = VAb/4 - qb2/32 - HAf/2 = 889.2·6/4 - 326.1·62/32 - 692.927·1.732/2 = 1333.8 - 366.86 - 600.075 = 366.863 кгм (268.1.7.2)
Ну а неточность в третьем знаке после запятой возникает из-за того, что для расчета мы принимаем значения величин округленные до второго-третьего знака после запятой. Но самое главное тут даже не это, а то, что формально мы вполне имеем право рассматривать любую стропильную ногу, как отдельную балку с опорами А и В (или В и С). Ну а итоговая опорная реакция VA (VC) и наличие горизонтальной опорной реакции HA (HC) - всего лишь результат совместной работы стержней.
Честно сказать, именно за это я сопромат и люблю, ну то есть за простоту и понятность, а также за возможность прийти к конечному результату разными способами, а заодно и проверить правильность выбранного способа, но не будем отвлекаться.
Как видим, даже без учета нормальных напряжений от продольной силы выбранного нами сечения не достаточно. Вариантов решения этой проблемы несколько:
а) Можно уменьшить шаг стропильных ног, что приведет к уменьшению расчетной нагрузки, однако при этом увеличится расход пиломатериалов и усложнится процесс монтажа кровли;
б) Можно уменьшить уклон кровли, что приведет к незначительному уменьшению пролета балки и соответственно к уменьшению значения изгибающего момента, но в данном случае разница между расчетным сопротивлением и действующим напряжением слишком велика и такая мера вряд ли поможет;
в) Можно увеличить сечение стропильных ног, например использовать брус сечением 200х50 мм, при этом момент сопротивления составит 5х202/6 = 333.33 см3, т.е. максимальные напряжения в сечении стропильной ноги составят
σ = 36686.2/333.33 = 110 кг/см2 < Rи = 140 кг/см2
Правда при этом увеличится вес стропильной ноги, однако при этом общая нагрузка увеличится очень незначительно;
Примечание: Если сделать затяжку выше опор арки, то это никак не влияет на расчетную длину пролета, а значит и на значение максимального изгибающего момента, только увеличивает напряжения в затяжке. Однако, как мы выяснили напряжения в затяжке итак не большие, а потому затяжку можно делать, исходя из размеров пиломатериала. Определить продольную силу, действующую на затяжку, до смешного просто: нужно в формулу (1.6) вместо стрелы арки f подставить расстояние по вертикали от затяжки до стрелы арки. Например, если поднять затяжку на половину высоты арки, то и продольная сила в затяжке увеличится в два раза.
Ограничимся тем, что пока примем расчетное сечение бруса 200х50 мм. При этом увеличится и коэффициент продольного изгиба φ = 0.65.
Таким образом максимальные нормальные напряжения в поперечном сечении посредине пролета левой части арки составят согласно формулы (214.3.1):
σ(N+M) = 800.15/(0.65·100) + 36686.2/333.3 = 12.31 + 110.06 = 122.37 кг/см2 < Rи =140 кг/см2.
Так как в наклонных стержнях арки возле узла В будут действовать нормальные сжимающие силы NA-B = NB-C = 800.15 кг, то при отсутствии точной прирезки в стреле арки нужно использовать деревянные накладки и при этом крепить их 800.15/87.5 = 9.1 а лучше 10 гвоздями диаметром 0.5 см. Впрочем, если учесть, что некоторый контакт между стропильными ногами в стреле арки все-таки будет, то можно ограничиться и 9 гвоздями. Ну а если стропила в стреле арки будут крепиться внахлест, то гвозди обязательны.
При ширине стропил b = 5 см длина опорной площадки стропил на мауэрлат должна составлять не менее F/b = 30/5 = 6 см.
Максимальный прогиб стропильных ног составит:
ф = 5ql4/384EI = 5·3.261·3004/384·105·3333.3 = 1.03 см
Примечание: Вообще-то прогиб рассчитывается не по расчетному, а по нормативному значению снеговой нагрузки, т.е. в данном случае значение прогиба будет меньше с учетом того, что коэффициент надежности по снеговой нагрузке составляет 1.4, тогда:
qпр(н) = (6.25 + 16.77 + 180·1.25·1.2/1.4)1.1 = 237.5 кг/м
соотношение:
qпр/qпр(н) = 326.1/237.5 = 1.373
Прогиб составит:
ф(н) = 1.03/1.373 = 0.75 см
На этом основной расчет можно закончить, если прогиб стропильных ног вас устраивает.
И еще, если изложенный здесь метод расчета вам не подходит, то можете попробовать рассчитать висячие стропила другим способом. | 
