Теоретические предпосылки расчета
Когда мы рассматривали виды нагрузок, то выяснили, что ударная нагрузка является одним из видов динамических нагрузок и отличается от статической нагрузки тем, что при определении максимальных напряжений следует учитывать силы инерции.
Ударной считается нагрузка, прикладываемая в очень короткий промежуток времени. Например, ударная нагрузка возникает при падении одного тела на другое или при быстром изменении давления между рассматриваемыми телами. Все это кажется довольно странным, ведь если тело, например гиря, имеет массу 32 кг, то масса гири не изменится ни до, ни после, ни в момент падения. И это действительно так, но только тогда, когда речь идет о гравитационной массе, однако тщательное исследование явлений окружающего мира показывает, что у любого тела есть еще и инертная или как ее еще называют - инерционная или инерциальная масса. А еще те же исследования показывают, что инертная масса равна гравитационной массе. Так вот, когда речь идет о ударных нагрузках, то создает такую нагрузку не гравитационная, а инертная масса. В общем курсе физики термин "нагрузка" не используется, а используется понятие "сила". И состояние многих материальных тел описывается взаимодействием различных сил. При этом все силы можно условно разделить на внешние и внутренние. В теоретической механике, теории сопротивления материалов, теории упругости, теории прочности и т.п. внешние силы, действующие на рассматриваемую конструкцию, рассматриваются, как нагрузки, а внутренние силы - как напряжения. При этом предполагается, что сумма внешних сил равна сумме внутренних сил, это в итоге и позволяет составлять уравнения равновесия для рассматриваемой системы.
Когда тело, создающее нагрузку, очень долго взаимодействует с телом, в котором под воздействием этой нагрузки возникают напряжения, то скорость обоих тел, точнее центров тяжести обоих тел, при таком взаимодействии согласно принятой системы отсчета практически не изменяется. Это позволяет рассматривать нагрузку и напряжения, как статические, т.е. обусловленные гравитационным взаимодействием. При ударе в зависимости от массы соударяемых тел, скорость одного из тел или обоих тел изменяется очень сильно и в сравнительно короткий промежуток времени. Одной из характеристик тела, двигающегося с некоторой скоростью, является импульс:
p = mиv (288.1)
В данном случае в виду имеется именно инертная масса, и рассматривается поступательное (прямолинейное) движение, т.е. такое движение, для корректного описания которого достаточно рассматривать движение только одной материальной точки, совпадающей с центром тяжести рассматриваемого тела. Для характеристики вращательного движения используются понятия момента инерции и угловой скорости, для сложного движения материальных точек изгибаемой конструкции - коэффициент жесткости, определяющий характер движения различных материальных точек, входящих в состав изгибаемой конструкции в зависимости от значений момента инерции, модуля упругости материала, действующей нагрузки и длины изгибаемой конструкции.
Когда тела сталкиваются с относительно большой скоростью, то из-за изменения скорости в течение короткого промежутка времени возникает ударная сила, точнее две ударные силы, одинаковые по значению и направленные противоположно. Таким образом рассматриваемая система сил по прежнему остается в равновесии:
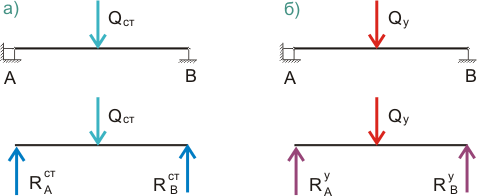
Рисунок 1. Равновесие сил рассматриваемой системы.
Если рассматривать тело, создавшее ударную нагрузку, то на него будет действовать ударная сила, равная сумме опорных реакций, показанных на рисунке 1.б) и равная - Qу, т.е. направленная противоположно. Однако строителей очень редко интересует судьба падшего тела, им необходимо обеспечить прочность конструкции после удара, т.е. рассчитываемая конструкция должна работать только в области упругих, восстанавливаемых со временем деформаций, а неупругие деформации, могут привести к разрушению конструкции.
Теоретически, если известно время t, в течение которого импульс будет передаваться от одного тела другому, определить ударную силу не проблема, так как
Qу = mиv/t (288.2)
и тогда расчет конструкции можно просто выполнить на действие ударной силы, т.е. по расчетной схеме, показанной на рисунке 1.б). Да вот беда, время, в течение которого импульс передается от одного тела другому, зависит от множества различных факторов (о которых речь ниже) и может измеряться в пределах от микросекунд до секунд. Потому точно определить значение времени, а значит и ударной силы достаточно сложно.
Далее, в процессе удара кинетическая энергия упавшего тела частично трансформируется в потенциальную энергию деформации рассматриваемой конструкции. Например балка, показанная на рисунке 1, прогнется, при этом в момент, когда значение деформации, будет максимальным, скорость движения центра тяжести балки будет равной нулю, а значит систему можно рассматривать как статическую. Вот только упавшее тело, если оно все еще находится на балке, уже не будет создавать ударную нагрузку, а только обычную статическую, поэтому внутренние напряжения начнут уменьшаться, а значит, и величина деформации будет уменьшаться. А в результате действия инерциальных сил, возникающих как при движении груза, так и при движении частиц рассматриваемой конструкции такое движение превратится в колебательное, со временем затухающее из-за перехода части кинетической и потенциальной энергии в тепловую.
Кроме того часть энергии удара преобразуется в звуковые колебания и если верить индийским фильмам, то в звук преобразуется чуть ли не вся энергия удара. Так же при ударе часть энергии переходит в упругие и неупругие деформации падающего тела и местные неупругие деформации рассматриваемого элемента конструкции, а потому точное решение задачи о возникающих при ударе внутренних напряжениях и деформациях материала конструкции с учетом вышеприведенных факторов является не простой задачей. Однако в точном решении задач не всегда есть необходимость и потому в строительной практике получили распространение приближенные методы расчета.
Максимально упростить решение подобных задач помогают следующие допущения и физические модели процесса:
1. Любую балку, плиту, стену, колонну или другую строительную конструкцию можно рассматривать как упругую систему с одной степенью свободы. Этим подразумевается, все деформации будут находиться в области упругих, т.е. восстанавливаемых со временем и то, что колебания будут происходить только относительно одной из осей. Например, при падении тела на рассматриваемую конструкцию под действием силы тяжести перемещение падающего тела происходит только вдоль оси у, возможные смещения тела вдоль осей х и z не учитываются. Некая тело с массой m, соединенное с упругой пружиной, является простейшей линейной механической моделью упругой системы с одной степенью свободы:
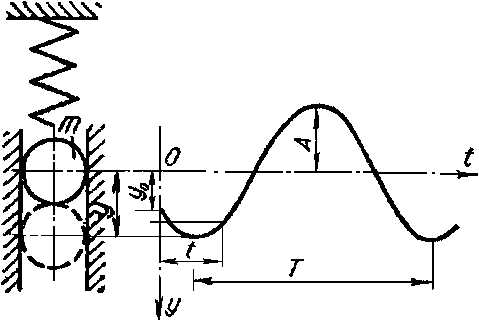
Рисунок 2. Амплитуда колебаний
2. Амплитуда колебаний, определяющая максимальное отклонение рассматриваемой точки вдоль оси у, соответствует максимальной деформации рассматриваемой конструкции. При продольном ударе - это относительное изменение длины Δl, при изгибающем ударе - прогиб f, при вращающем ударе - угол поворота φ (далее мы будем рассматривать в основном изгибающий удар). При рассмотрении колебательного движения физических тел, двигающихся по прямолинейной траектории, рассматриваемая точка, совершающая колебания, соответствует центру тяжести тела, если масса изгибаемой конструкции пренебрежимо мала, по сравнению с массой ударяющего тела, то для упрощения расчетов массой изгибаемой конструкции можно пренебречь и рассматривать колебания согласно принятой физической модели (рисунок 2).
3. Так как колебания системы, вызванные ударом, являются затухающими из-за сопротивления окружающей среды (как минимум воздуха) и наличия сил внутреннего трения, постепенно переводящих часть энергии удара в нагрев, то максимальная амплитуда, соответствующая максимальной деформации, будет только в течение первого периода колебания. Таким образом расчет сводится к определению максимально возможной амплитуды в течение первого периода колебания.
4. Деформации рассматриваемого элемента конструкции от ударяющего тела распространяются по всей длине элемента, подчиняются закону Гука и пропорциональны деформациям, которые возникают при статическом приложении нагрузки от того же тела и в том же месте, т.е. расчетные схемы, показанные на рисунке 1, могут использоваться для расчета рассматриваемой конструкции.
5. Пропорциональность динамических и статических деформаций δ определяется динамическим коэффициентом удара kд, соответственно пропорциональность динамических и статических напряжений σ также определяется динамическим коэффициентом:
δд = kдδст (288.3.1)
σд = kдσст (288.3.2)
соответственно
Qд = kдQст (288.3.3)
Мд = kдМст (288.3.4)
и так далее.
6. Предполагается, что падающее тело имеет жесткость значительно больше жесткости рассматриваемого элемента конструкции. Это позволяет не учитывать величину упругих деформаций падающего тела при ударе и соответственно исключает развитие неупругих деформаций в упавшем теле. Соответственно время, в течение которого импульс от одного тела передается другому будет минимальным, а значит и значение ударной силы будет максимально возможным. И даже если на железную балку падает железная гиря, имеющая вполне определенную жесткость, то для упрощения расчетов упругие и возможные неупругие деформации гири не учитываются. Результат такого допущения - дополнительный запас по прочности.
7. Предполагается, что падающее тело с момента прикосновения к рассматриваемому элементу конструкции продолжает движение с такой же скоростью, с какой перемещается поперечное сечение элемента под телом в результате развития деформаций, т.е. упавшее тело как бы прилепляется к рассматриваемому элементу и не отскакивает до момента развития максимальных деформаций. Такое допущение справедливо лишь тогда, когда масса упавшего тела не меньше массы элемента. А если масса рассматриваемого элемента пренебрежимо мала по сравнению с массой падающего тела, то в момент столкновения изменением скорости вообще можно пренебречь и рассматривать изменение скорости упавшего тела после столкновения только как результат изменения потенциальной энергии деформации и тогда принятая физическая модель будет наиболее полно соответствовать реальному процессу. Если масса рассматриваемого элемента равна или больше массы падающего тела, то такое допущение также приводит к дополнительному запасу по прочности.
8. Явление удара рассматривается с позиций закона сохранения энергии и соответственно сохранения импульсов. При этом предполагается, что кинетическая энергия Т1 падающего тела - груза в момент удара полностью превращается в потенциальную энергию Uд2 деформации конструкции и кинетическую энергию Т'2 движения рассматриваемой конструкции:
Е = Т1 = Uд2 + Т'2 (288.4.1)
Это допущение справедливо только при рассмотрении столкновения двух равноупругих тел имеющих равную массу, при этом одно из тел до момента столкновения находится в состоянии покоя, т.е. его скорость равна нулю. Поэтому количество кинетической энергии рассматриваемой конструкции Т2 принимается равным нулю, а также принимается равным нулю количество кинетической энергии Т'1 падающего тела сразу после момента столкновения, так как скорость падающего тела в момент столкновения обнуляется.
Если масса рассматриваемого элемента конструкции пренебрежимо мала по сравнению с массой ударяющего тела, то величиной Т2 для упрощения расчетов можно пренебречь и рассматривать изменение кинетической энергии падающего тела как изменение потенциальной энергии деформации рассматриваемого элемента:
Т = Uд (288.4.2)
Это допущение, не учитывающее переход части энергии в звуковую, тепловую и другие воды энергии также дает дополнительный запас по прочности.
Принятие этих допущений позволяет значительно упростить расчет конструкций и даже обеспечить дополнительный запас по прочности для колонны, стойки, балки, плиты и любого другого рассматриваемого элемента конструкции при использовании физической модели, показанной на рисунке 2.
В зависимости от направления удара по отношению к оси рассматриваемого элемента конструкции и характера происходящих деформаций удары рассматриваются как продольный - приводящий к растяжению или сжатию рассматриваемого элемента (колон, стоек, стен, свай), поперечный - вызывающий деформации изгиба (поперечный удар часто называют изгибающим ударом) характерен для стержней, балок, плит перекрытия, и крутильный удар - вызывающий деформации кручения в валах машин и механизмов или в балках при внецентренном приложении ударной нагрузки.
Теория расчета на динамическую нагрузку
Согласно основному закону динамики - второму закону Ньютона - любое тело, имеющее некоторую массу m и движущееся с ускорением свободного падения g = 9.81 м/с2, может рассматриваться как сила Q = mg, а при расчете строительных конструкций внешние силы, как уже говорилось, рассматриваются, как нагрузка. Именно поэтому в формулировке задач по расчету строительных конструкций нагрузки от тел, имеющих некоторую массу m, измеряемую в понятных простому человеку килограммах или тоннах , указываются в не столь хорошо известных и понятных Ньютонах и килоНьютонах. Теоретически это правильно, но вполне допустимо при выполнении расчетов заменять Ньютоны на килограмм-силы. Например, человека весом в 100 кг, можно рассматривать как сосредоточенную нагрузку Q = 1000 Н = 100 кгс или просто 100 кг. При этом уменьшение значения, возникающее при умножении массы на 9.81 обычно не учитывается, что опять таки приводит к дополнительному запасу по прочности.
При этом даже если человек стоит абсолютно неподвижно в течение долгого времени, т.е. скорость его перемещения в рассматриваемой системе отсчета равна нулю, то он все равно создает нагрузку, в данном случае статическую. Этот парадокс устраняется тем, что если опору из под человека убрать, то он полетит к центру Земли, причем с ускорением, мало отличающимся от ускорения свободного падения и значит опора может рассматриваться как такая же сила, только действующая в противоположную сторону, и называется эта сила опорной реакцией. А когда опорная реакция равна опорной силе, то система находится в состоянии равновесия, т.е. никуда не движется (во всяком случае в принятой системе отсчета). При рассмотрении стержней и балок, имеющих две опоры, таких опорных реакций будет две (см. рисунок 1).
Однако все это справедливо только для абсолютно жестких тел. Реальные же тела и в частности строительные конструкции под воздействием нагрузки деформируются, а значит и человек, представляющий собой нагрузку, будет перемещаться в пространстве на величину этой деформации.
Как определяются деформации для сжатых, растянутых и изгибаемых элементов, и при чем тут момент инерции, мы уже знаем, осталось только добавить, что при расчете деформаций от действия статической нагрузки предполагается, что статическая нагрузка прикладывается не моментально, а очень медленно, т.е. значение нагрузки постепенно нарастает от нуля до максимального значения за время, значительно превышающее время деформации. Таким образом скорость перемещения в пространстве тела, создающего нагрузку, стремится к нулю и получается, что наблюдаемые в результате воздействия нагрузки деформации, например вот такие:

Фотография 174.1. Прогиб балки - линейки при действии статической нагрузки - мерного стакана
это результат действия только гравитационной массы тела, создающего нагрузку. Дальнейшее описание будет производиться на примере балки линейки для наглядности.
Если приложить нагрузку мгновенно, например, если поставить мерный стакан на линейку и сразу его отпустить, то прогиб будет значительно больше. Потому что стакан, опускаясь вместе с прогибающейся линейкой, на определенном этапе приобретет достаточно большую скорость, а значит, при расчетах нужно учитывать не только гравитационную, но и инертную массу тела, а также инертную массу рассматриваемой конструкции. Так как физиками до сих пор считается, что гравитационная масса равна инертной (во всяком случае попытки опровергнуть это утверждение пока ни к чему не привели), то вполне логично предположить, что инертная масса приведет к такой же деформации как и гравитационная масса, а значит деформация от динамической нагрузки будет в 2 раза больше, чем от статической нагрузки, создаваемой тем же телом. В математическом выражении это предположение с учетом теоретических предпосылок (т.е. без учета массы линейки) выглядит так:
- для статической нагрузки kд = 1
- для динамической нагрузки kд = 1 + 1 = 2
Впрочем, такой метод определения динамического коэффициента при мгновенном приложении нагрузки может показаться слишком простым. Что ж, устранить эту проблему не сложно. Для начала вернемся к п.2 и 3 теоретических предпосылок и рассмотрим их более детально.
В общем виде уравнение гармонических колебаний, позволяющее определить значение отклонения по оси у - что в нашем случае соответствует величине деформации f, выглядит так:
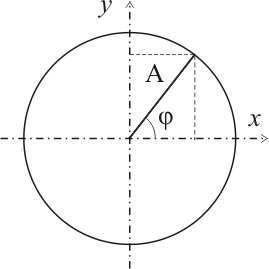
Рисунок 3. Амплитуда колебаний, как радиус окружности и гипотенуза прямоугольного треугольника
у = Аsinφ = Asin(φo + ωt) (288.5.1)
где φ = φo + ωt - фаза колебания, соответственно φo - начальная фаза колебания при t =0.
При этом амплитуда рассматривается, как радиус окружности, а фаза колебаний, как угол наклона этого радиуса, что в итоге и дает нам синусоиду для исследуемой точки, показанную на рисунке 2. Так как скорость материальной точки является производной расстояния по времени, то
y' = v = (Asin((φo + ωt))' = Aωcos(φo + ωt) (288.5.2)
тогда значение амплитуды по оси х можно рассматривать как t = v/ω. Ну а дальше из установленных Архимедом соотношений сторон прямоугольного треугольника, образованного катетами х и у и гипотенузой А, следует, что:
А = √¯(у2 + х2) = √¯(у2 + (v/ω)2) (288.5.3)
Если придать этой легкой математической формуле тяжелый физический смысл, то получается, что максимальное значение отклонения по оси у, а в нашем случае величина деформации f, будет максимальным, когда скорость материальной точки - стакана будет равна нулю и соответственно максимальная скорость у материальной точки будет в моменты, когда деформация будет равна нулю. Причина этого - в воздействии сил инерции. Так как нас интересует только максимальное значение отклонения, равное амплитуде, т.е. у = А, т.е. при скорости материальной точки, равной нулю, то формулу (288.5.3) можно с учетом этого преобразовать в:
А = √‾(yи2) (288.5.4)
где уи - максимальное значение деформации при действии сил инерции. При этом полное значение деформации с учетом действия гравитационных сил (на примере линейки) составит:
fп = fг + fи = 2fг = 2fи = fг + √¯(fг2) (288.6.1)
Так как прогиб от действия инертной массы равен прогибу от действия гравитационной массы.
Соответственно динамический коэффициент составит
kд = 1 + 1 = 1 + √¯(12) = 2 (288.6.2)
Если вернуться к математической модели, то мы как бы смещаем вниз по оси у синусоиду (рисунок 2) или окружность (рисунок 3) на значение уг, равное уи, и таким образом получаем полное значение деформации в точках экстремума функции.
Таким образом человек, который ходит по помещению и при этом достаточно быстро перебирает ногами, перенося свой вес с одной ноги на другую, создает как минимум динамическую нагрузку и потому при расчете конструкций перекрытия на нагрузку от такого человека статическую нагрузку, создаваемую гравитационной массой человека, следует умножать на динамический коэффициент kд = 2. При этом высота падения и соответственно скорость падения в момент столкновения принимаются равными нулю.
Теория расчета на ударную нагрузку
До этого мы рассматривали деформацию тела (балки) под действием динамической нагрузки, т.е. в ситуации, когда скорость груза в момент касания с конструкцией равна нулю. Если же груз будет падать с некоторой высоты, то в момент касания с конструкцией эта скорость не будет равна нулю (при принятой нами массе балки значительно меньшей, чем масса груза) и тогда для определения амплитуды теоретически можно использовать формулу (288.3.3). Вот только для этого придется сначала определить значение скорости в момент удара.
Скорость тела, падающего с ускорением свободного падения, без учета влияния сопротивления окружающей среды в любой момент времени можно определить по формуле:
v = √¯(vo2 + 2gh) (288.7.1)
где h - высота падения, м.
Если начальная скорость vo = 0, то формула (288.6.1) примет вид
v = √(2gh) (288.7.2)
Теперь попробуем определить значение циклической частоты ω (или угловой скорости - это кому как больше нравится). Так как ускорение - это вторая производная расстояния по времени, то:
y'' = a = (Asin((φo + ωt))'' = - Aω2sin(φo + ωt) (288.8)
Физический смысл этой формулы в том, что ускорение движения тела а, подобно скорости v и величине смещения y, подчиняется гармоническому закону, но колебания ускорения на полпериода (на угол П) расходятся с колебаниями смещения и находятся как бы в противофазе смещению. То есть когда смещение (в нашем случае прогиб f) максимально, то ускорение а также максимально, но направлено в сторону, противоположную смещению. Так же здесь заметим, что колебания скорости смещены на четверть периода или на угол П/2, по отношению к колебаниям смещения.
Таким образом из формул (288.3.1) и (288.7) можно вывести уравнение гармонических колебаний:
a/ω2 + y = 0 или у'' + ω2y = 0 (288.9)
соответственно
ω2 = - [a/y] или ω2 = Q/my = g/yи (288.10.1)
В данном случае имеется в виду инертная масса груза, а масса балки не учитывается. Тогда согласно формул (288.5.3), (288.7.2) и (288.10.1)
у = √¯(уи2 + 2ghyи/g) = √¯(уг2 + 2hyг) (288.11.1)
Тогда полное значение деформации составит:
уп = уг + √¯(уг2 + 2hyг) (288.11.2)
тогда
kд = уп/уг = 1 + √1 + 2h/yг = 1 + √1 + 2h/уст (288.11.3)
Как правило никакой разницы между деформациями от динамической и ударной нагрузки не делается, а динамическая нагрузка рассматривается как частный случай ударной нагрузки, при которой скорость падающего груза в момент контакта с рассматриваемой конструкцией равна нулю, понятие "ударный коэффициент" - не используется, величина деформации от действия гравитационной массы обозначается как статическая деформация уст. Сути дела это не меняет, но упомянуть об этом стоит, равно как и о том, что формулы (288.11) можно вывести и другими способами. Здесь же приведен, возможно и не самый простой, но по моему мнению самый наглядный способ. И еще, если присмотреться, то формулы для определения скорости, вертикального смещения, и многих других не приведенных здесь параметров, достаточно похожи, а роднит их принцип определения гипотенузы прямоугольного треугольника. Вот такие дела.
Если вернуться к математической модели, то при определении амплитуды при ударной нагрузке мы рассматривали как бы не всю, а только нижнюю часть синусоиды, при этом амплитуда рассматриваемой синусоиды соответствует амплитуде колебаний, создаваемой при динамической нагрузке грузом, имеющим массу, умноженную на динамический коэффициент.
Для упрощения расчетов при h/yст > 10 единицей в подкоренном выражении можно пренебречь и тогда формула (288.11.3) примет вид:
kд = 1 + √2h/уст (288.11.4)
А если h/yст > 100, то можно не учитывать и единицу перед квадратным корнем, тогда:
kд = √2h/уст (288.11.5)
Пример расчета балки на ударную нагрузку
Имеется шарнирно закрепленная балка перекрытия длиной 4 м из древесины сечением 20х10 см. На средину балки с высоты 50 см падает гиря весом в 32 кг. Требуется определить прочность балки при ударной нагрузке.
1. Определим прогиб балки при воздействии статической нагрузки
fcт = Ql3/48EI = 32х4003/(48х100000х6666.667) = 0.064 см
где Е = 105 кгс/см2 - модуль упругости древесины, I = bh3/12 = 6666.667 см4 - момент инерции поперечного сечения.
2. Если определять динамический коэффициент с учетом того, что высота падения значительно больше статического прогиба, то
kд = 1 + √(2х50/0.064) = 40.53
3. Тогда максимальный прогиб составит
fд = 0.064х40.53 = 2.59 см
4. Это достаточно большой прогиб, но намного важнее выяснить, выдержит ли такую ударную нагрузку балка
Мд = Qlkд/4 = 32х400х40.53/4 = 129696 кг·см
5. Тогда при расчетном сопротивлении R = 140 кг/см2 требуемый момент сопротивления составит
Wтр = М/R = 129696/140 = 926.4 см3
6. Момент сопротивления для балки сечением 20х10 см составит W = 2I/h = 6666.667/10 = 666.67см3 < Wтр = 926.4 см3.
Вывод: балка под действием такой ударной нагрузки разрушится.
Пример расчета балки на ударную нагрузку от груза, падающего не посредине балки
Имеется все та же шарнирно закрепленная балка перекрытия длиной 4 м из древесины сечением 20х10 см. На расстоянии 1 м от опоры балки с той же высоты 50 см падает все та же гиря весом в 32 кг. Требуется определить прочность балки при ударной нагрузке.
1. Определим прогиб балки в месте падения груза при воздействии статической нагрузки
fcт = Qа2b2/3lEI = 32х1002x3002/(3х400x100000х6666.667) = 0.036 см
kд = √2х50/0.036 = 52.7
как видим, за счет смещения места падения груза к одной из опор динамический коэффициент даже увеличился, но нас по прежнему интересует прочность балки
Мд = Qabkд/l = 32х100x300х52.7/400 = 126491 кг·см
так как максимальное значение изгибающего момента почти не изменилось, то и без дальнейших расчетов понятно, что балка такую ударную нагрузку не выдержит. А вот если груз упадет очень близко к одной из опор, например на расстоянии 10 см, то
fcт = Qа2b2/3lEI = 32х102x3902/(3х400x100000х6666.667) = 0.00061 см
kд = √2х50/0.00061 = 405.42
Мд = Qabkд/l = 32х10x390х229.4/400 = 126491 кг·см
Вывод: на каком бы расстоянии от опоры ни упал груз, балка под действием такой ударной нагрузки разрушится.
Пример расчета балки на ударную нагрузку с учетом жесткости падающего груза
Как видим, если рассматривать соударение балки с гирей, как абсолютно жестким телом, то у балки никаких шансов на выживание нет, она разрушится. Однако любое физическое тело имеет вполне определенную жесткость, а это значит, что такое тело будет также деформироваться. А значит, время контакта при столкновении двух тел из-за упругих и возможных неупругих деформаций ударяющего тела будет больше и соответственно ударная сила, действующая на балку, будет меньше. Это подтверждают эксперименты со сталкивающимися телами из любых материалов. Например, когда относительно легкий стальной шарик падает на очень массивную стальную пластину, то теоретически после соударения относительно легкий металлический шарик должен отскочить от очень массивной пластины на высоту, примерно равную высоте, с которой шарик упал. Однако в реальности высота отскока значительно меньше, и разница доходит до 3 раз. На основании этого можно определить коэффициент восстановления:
kв = √h'/h (288.12)
где h' - высота отскока, а h - высота падения.
Этот коэффициент будет показывать, насколько уменьшится ударная сила с учетом упругих свойств падающего груза и тогда
kуд = 1 + √1 +2h'/fстили kyд = kдkв (288.13)
ниже приведены значения коэффициента восстановления для некоторых веществ:
Таблица 1. Коэффициенты восстановления при частично упругом соударении тел
| Вещество |
k |
| Древесина |
0.5 |
| Пробка |
0.55 |
| Сталь |
0.55 |
| Слоновая кость |
0.889 |
| Стекло |
0.9375 |
Помимо всего прочего изучение этой таблицы позволяет понять, почему раньше для изготовления бильярдных шаров использовалась именно слоновая кость. Но в данном случае нас интересует сталь, точнее гиря изготовленная с применением железа. Конечно же на значение коэффициента восстановления будет влиять геометрическая форма падающего тела, и чем ближе эта форма к шару тем ближе значение коэффициента восстановления к указанному в таблице. Поэтому значение коэффициента восстановления следует дополнительно умножить на поправочный коэффициент kп = 0.5 - 1, учитывающий форму падающего тела в зависимости от материала сталкивающихся тел. Определение более точного значения поправочного коэффициента - отдельная большая тема. Однако для упрощения расчетов лучше не уменьшать значение коэффициента восстановления, а наоборот увеличить, умножив на коэффициент надежности по нагрузке γ = 1.1 - 1.3.
Например, при столкновении железной гири с деревянной балкой можно использовать коэффициент γ = 1.2 и тогда:
kд = 40.53х0.55х1.2 = 26.75
тогда максимальный прогиб составит
fд = 0.064х26.75 = 1.71 см
Мд = Qlkд/4 = 32х400х26.75/4 = 85600 кг·см
Wтр = М/R = 85600/140 = 611.4 см3
момент сопротивления W = 6666.667/10 = 666.67см3 > Wтр = 611.4 см3.
Вывод: балка выдержит такую ударную нагрузку, однако существует очень высокая вероятность того, что после удара на поверхности балки останется порядочная вмятина, а выражаясь научным языком, изменятся размеры поперечного сечения балки, что приведет к изменению несущей способности балки. Поэтому даже если балка и выдержит один удар, то нет никакой гарантии, что балка выдержит много ударов и такую балку желательно избавить от такого насилия. Обычно это происходит по умолчанию, когда на балки перекрытия укладываются доски напольного покрытия. И тогда в результате падения тяжелых грузов с относительно большой высоты будет страдать уже не балка, а точнее не только балка, но и доски, а если это доски чернового пола, то покрытие по черновому полу. А потому обычно выполняется дополнительная защита пола в местах, где падение груза на перекрытие достаточно вероятно. Принцип такой защиты прост - чем толще защитное покрытие и чем меньше модуль упругости материала защитного покрытия, тем меньше будет в итоге ударная сила, действующая на конструкции перекрытия. Да и поменять защитное покрытие намного быстрее и дешевле, чем балки или плиты перекрытия.
Кстати на эффекте развития местных неупругих деформаций основаны различные методы неразрушающих методов определения прочности бетона, в частности для этого может использоваться молоток Кашкарова, но это уже совсем другая тема.
И еще, борцы тоже не любят бороться на жестком бетонном полу, а все больше на специальных покрытиях и вовсе не потому, что заботятся о надежности перекрытия, в этом случае за основу берется прочность главной несущей конструкции человеческого организма - скелета и в частности черепа. | 
