1. Любое тело, если свобода его передвижения не ограничена, может перемещаться в пространстве, как ему заблагорассудится. Закономерности движения таких тел изучает кинематика, а возникновение и влияние сил, к такому движению приводящих - удел динамики. В трехмерном мире, в котором мы живем, существует свобода перемещений в трех направлениях вверх-вниз, вперед-назад и вправо-влево, или три степени свободы. Соответственно, чтобы ограничить свободу передвижения в этих трех направлениях или, выражаясь геометрическим языком - в этих трех плоскостях, исследуемое тело нужно связать с каким-нибудь другим неподвижным телом и количество таких связей, именуемых кинематическими, должно быть не менее трех. Но и это еще не все, если кинематические связи не защищают от возможности вращения, то у тела остается еще 3 степени свободы - вращаться в трех плоскостях и потому на физическое тело нужно наложить 6 связей, чтобы полностью ограничить его свободу. И если задача мудрого правителя - ограничивать свободу передвижения человеческих тел, являющихся одновременно и физическими телами, таким образом, чтобы при этом оставалась полная иллюзия свободы, то задача мудрого строителя - проектировать строительные конструкции так, чтобы создавалась полная иллюзия отсутствия свободы перемещений. Такое состояние строительной конструкции называется статическим равновесием, а кинематические связи рассматриваются как опоры.
2. Одним из видов строительных конструкций являются балки. Балки с точки зрения строительной механики рассматриваются как стержни, т.е. такие физические тела, высота и ширина которых значительно меньше длины. Для решения множества задач рассматривать балку как объемное физическое тело вовсе не обязательно, вполне достаточно ограничиться рассмотрением "плоской" задачи, т.е. рассматривать балку, как некий условно плоский и даже одномерный стержень (влияние геометрических размеров поперечных сечений балки учитывается на следующем этапе расчета). Таким образом для ограничения свободы плоского стержня необходимо наложить 4 кинематических связи. А если учесть, что балка сама по себе есть связь между своими точками, то количество связей можно уменьшить до 3. При этом две связи (показаны на рисунке 219.2 фиолетовым цветом) ограничивают перемещение относительно оси у, а одна связь (показана на рисунке 219.2 синим цветом) и сама балка, имеющая некоторую жесткость, ограничивают перемещения по оси х:
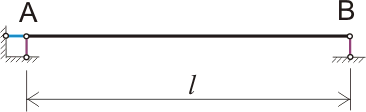
Рисунок 219.2. Шарнирно опертая безконсольная балка.
При этом нельзя забывать, что реальная балка перекрытия или плита, опертая на стены дома, и шарнирно опертая безконсольная балка, показанная на рисунке 219.2 - это принципиально разные вещи. А для значительного упрощения расчетов допускается предполагать, что реальная балка соответствует данной расчетной схеме.
3. Для расчета любой строительной конструкции необходимо знать значение всех сил, действующих на конструкцию.
4. Предполагается, что любое тело, в нашем случае балка, имеющая опоры, будет оставаться в состоянии статического равновесия после замены кинематических связей - опор - соответствующими реактивными силами, или как их чаще называют - опорными реакциями. На основании этого можно составить 2 уравнения равновесия системы, относительно оси х и относительно оси у.
∑у = 0 - для сил, действующих вдоль оси у. (253.1.1)
∑х = 0 - для сил, действующих вдоль оси х. (253.1.2)
Однако этих двух уравнений для определения трех неизвестных явно недостаточно, нужно составить еще хотя бы одно уравнение.
5. Сделать это помогает переход на следующий уровень, когда рассматриваются не сами силы, а моменты, этими силами создаваемые. Как то установил Архимед, чем больше расстояние от точки приложения силы до рассматриваемой точки, тем больше значение момента. Соответственно, если есть некая надежная точка опоры, то если на эту точку опереть некий стержень таким образом, чтобы длина стержня с одной стороны (длинное плечо) была много больше длины с другой стороны (короткое плечо), а затем приложить к концам стержня некоторые силы, то стержень будет оставаться в состоянии равновесия, если сила, приложенная к длинному плечу, будет меньше силы, приложенной к короткому плечу, во столько раз, во сколько длинное плечо длиннее короткого плеча. А если значение силы, приложенной к длинному плечу будет хотя бы немного больше, то стержень начнет вращаться относительно точки опоры. Отсюда и проистекает знаменитое высказывание Архимеда: "дайте мне точку опоры и я переверну мир". И хотя надежную точку опоры Архимеду так никто и не дал, да и стержень, который Архимед намеревался использовать в качестве рычага, следовало бы просчитать на прочность, тем не менее открытие Архимеда мир действительно перевернуло и теперь этим открытием пользуются не только инженеры, рассчитывающие строительные конструкции, но и все другие люди, пользующиеся фомкой.
Если рассматривать открытие Архимеда с позиции строительной механики, то точка приложения сосредоточенной нагрузки, центр тяжести распределенной нагрузки или приведенный центр тяжести всех приложенных к балке нагрузок - это и есть та точка опоры, относительно которой момент, создаваемый реактивной силой правой опоры, равен моменту, создаваемому реактивной силой левой опоры, а сама балка находится в состоянии статического равновесия. Если перевести открытие Архимеда на математический язык, то момент - есть некая функция у = f(x), М = Qx или М = ∫Qdx. На основании этого можно составить как минимум одно дополнительное уравнение, позволяющее определить значение одной из опорных реакций. Например, для шарнирно закрепленной балки значение изгибающего момента в точке приложения первой силы и в точке приложения последней силы будет равно нулю.
Если бесконсольная балка длиной l имеет шарнирно неподвижную опору А и шарнирно подвижную опору В (см. рис.219.2), и к этой балке приложена только сосредоточенная нагрузка Q на расстоянии х от опоры В, то уравнение моментов в точке В, исходя из условия статического равновесия, будет иметь следующий вид:
МB = Аl - Qx = 0 (253.1.3)
Таким образом любая "плоская" строительная конструкция, имеющая 3 кинематические связи (не пересекающиеся в одной точке, что обеспечивает геометрическую неизменяемость системы) и некоторую жесткость, находится в состоянии статического равновесия, а для определения опорных реакций такой конструкции достаточно 2 уравнений равновесия системы и одного уравнения моментов.
6. Между тем у балки, как и у любой другой строительной конструкции, может быть не 3 кинематических связи, а 4, 5, 10 и вообще сколь угодно много. Причем балке от этого только лучше, так как чем меньше расстояние между опорами, тем больше несущая способность при тех же геометрических параметрах сечения и прочностных характеристиках. А вот для человека, занимающегося расчетом конструкций, в этом ничего хорошего нет, так как каждая связь сверх трех, обеспечивающих статическое равновесие, является как бы лишней. Количество "лишних" кинематических связей называется степенью статической неопределимости. Определить дополнительные реактивные силы - опорные реакции для таких связей, пользуясь уравнениями равновесия и уравнением моментов, невозможно, нужно составить столько дополнительных уравнений, сколько имеется лишних опор.
7. Сделать это опять помогает переход на следующий уровень, когда дополнительно рассматриваются углы поворота поперечных сечений или прогибы - вертикальные перемещения центров тяжести поперечных сечений балки. Как и изгибающие моменты, углы поворота θ и прогибы f зависят от величины прикладываемой нагрузки и в общем виде эту зависимость можно выразить так:
θ = ∫Мdx/EI = ∫∫Qd2x/EI (314.1.1)
f = ∫θdx = ∫∫Md2x/EI = ∫∫∫Qd3x/EI (314.1.2)
Так как вертикальная шарнирная опора не препятствует повороту, но препятствует вертикальному перемещению (для того она и используется), то сколько бы ни было у балки опор и как бы хитроумно ни была приложена к балке нагрузка, вертикальные перемещения - прогибы - на вертикальных опорах всегда будут равны нулю.
Примечание: Здесь опять же не следует забывать, что в действительности дополнительные вертикальные опоры далеко не всегда обеспечивают отсутствие прогибов на этих опорах. Например, монолитное железобетонное перекрытие по балкам может рассматриваться как многопролетная балка на шарнирных опорах весьма условно, так как балки - промежуточные опоры - под действием нагрузки, передаваемой плитой, также будут прогибаться и потому такую плиту более правильно рассматривать, как балку с крайними шарнирными опорами и промежуточными упруго деформируемыми опорами. Однако это будет после, а нам бы пока разобраться, как рассчитать статически неопределимую балку на шарнирных опорах.
8. Так как прогибы на всех вертикальных шарнирных опорах равны нулю, то любую статически неопределимую балку можно рассматривать как статически определимую, на которую действуют дополнительные силы - неизвестные опорные реакции. Причем действуют таким образом, что прогиб в точках приложения таких сил равен нулю. Это предположение позволяет составить столько дополнительных уравнений, сколько имеется "лишних" связей.
Такой метод расчета называется методом сил (или методом нулевых линейных перемещений)
Рассмотрим, как это делается, на следующем примере:
Имеется двухпролетная неразрезная балка с постоянной жесткостью EI по длине балки, к которой приложена равномерно распределенная нагрузка:
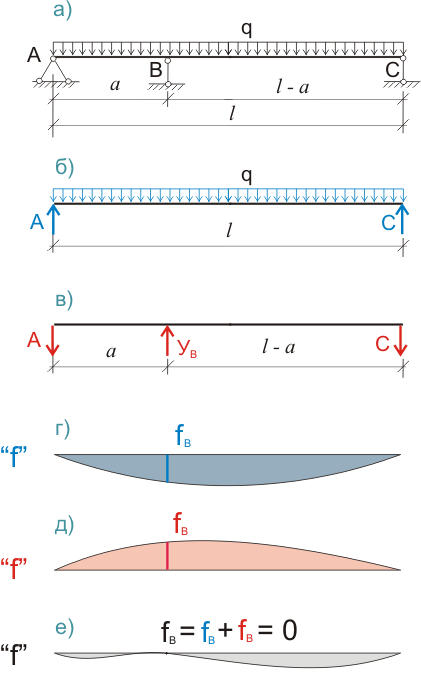
Рисунок 314.1. Приведение 1 раз статически неопределимой балки к основной и вспомогательной системам.
Такую балку можно рассматривать как обычную однопролетную, а значит, статически определимую балку, показанную на рисунке 314.1.б). Такая балка рассматривается как элемент основной системы. Определить для такой балки опорные реакции, построить эпюры поперечных сил, изгибающих моментов, углов поворота и прогиба - не проблема. В данной статье принципы построения эпюр не рассматриваются, а эпюры поперечных сил, моментов и углов поворота не приводятся, так как нас в данном случае интересует только эпюра прогибов, показанная на рисунке 314.1.г).
Балка, показанная на рисунке 314.1.в) - это элемент вспомогательной системы, которая также является статически определимой и также легко может рассчитываться как и основная система. А неизвестная опорная реакция УВ определяется, исходя из принятого нами условия - прогиб балки на опоре В fB = 0.
В частном случае, когда промежуточная опора В находится посредине основного пролета, т.е. а = l/2, определение неизвестной опорной реакции много времени не займет, так как при действии равномерно распределенной нагрузки
fl/2 = - 5ql4/(384EI) (174.6.4.6)
Соответственно реакции опор для балки основной системы
А = С = ql/2 (314.2.1)
а при действии сосредоточенной нагрузки посредине пролета
fl/2 = УВl3/(48EI) (174.6.3.5)
Для такой балки реакции опор составят
А = С = - УВ/2 (314.2.2)
и тогда из уравнений (174.6.4.6) и (174.6.3.5) следует, что
5ql4/384EI = УВl3/48EI (314.2.3)
УВ = B = 5ql/8 = 10qa/8 (314.2.4)
Таким образом мы определили неизвестную опорную реакцию В. Соответственно остальные расчетные реакции опор для балки
А = С = А + А = ql/2 - 5ql/16 = 3ql/16 = 3qa/8 (314.2.5)
А момент на средней опоре
M = 3ql2/32 - ql2/8 = - ql2/32 = 3qa2/8 -qa2/2 = - qa2/8 (314.3.1)
Во всех остальных случаях, т.е. когда промежуточная опора находится не посредине пролета, отделаться столь малой кровью уже не получится. Сначала следует определить значение прогиба для основной системы и хотя нагрузка для основной системы не изменится, но изменится положение поперечного сечения, для которого следует определить прогиб.
при х = а
fа = - θAа + Aа3/6EI - qа4/24ЕI = q(2lа3 - а4 - l3а)/24EI (314.3.1)
Для вспомогательной системы - балки к которой сосредоточенная нагрузка - неизвестная опорная реакция будет приложена не посредине пролета, уравнение прогиба для точки приложения нагрузки будет иметь вид
fa = УВа2(l -a)2/3lEI (314.3.2)
а опорные реакции составят
А = - УВ(l - a)/l; C = - УВа/l (314.3.3)
и тогда
УВ = В = ql(2lа3 - а4 - l3а)/(8а2(l -a)2) (314.3.4)
Как видим, при смещении дополнительной опоры относительно центра балки определение опорных реакций значительно усложняется.
А если у балки будет не одна "лишняя" опора, а две, то нам придется задействовать вторую вспомогательную систему - балку с нагрузкой, приложенной на второй "лишней" опоре:
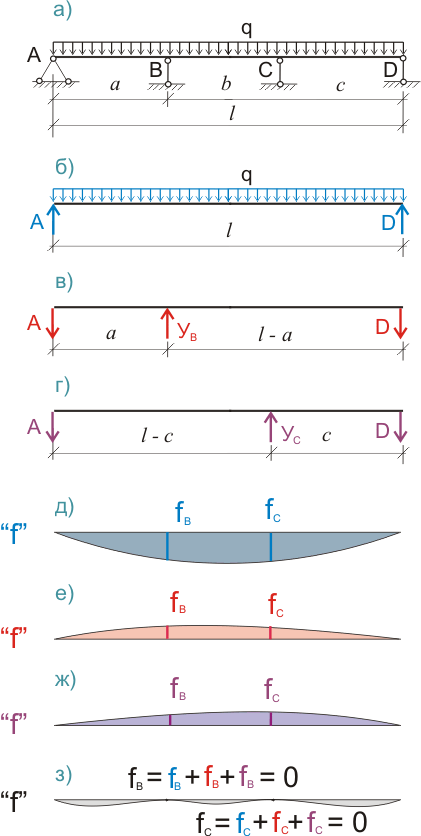
Рисунок 314.2. Приведение дважды статически неопределимой балки к основной и вспомогательной системам.
А еще это означает, что мы не сможем сразу определить значение одной из неизвестных опорных реакций. Для того, чтобы это сделать, необходимо решить систему из двух уравнений, показанных на рисунке 314.2.з).
А так как статически неопределимых реакций опор может быть сколь угодно много, так что цветов на все не напасешься, да и не всегда есть возможность показать эту разницу цветом, то подобные уравнения записываются в несколько иной форме:
fв0 + fвУв + fвУс = 0 (314.4.1)
fс0 + fсУв + fсУс = 0
А если обозначить статически неопределимые опоры цифрами, а прогиб греческой буквой Δ, то система уравнений будет выглядеть так:
Δ10 + Δ1У1 + Δ1У2 = 0 (314.4.2)
Δ20 + Δ2У1 + Δ2У2 = 0
Это и есть канонические уравнения описанного выше метода сил (метода нулевых линейных перемещений)
Если у балки будет 3 статически неопределимых опоры, то нужно составлять систему из трех уравнений, в каждом из которых будет по 3 неизвестных величины. Для балки с 5 статически неопределимыми опорами потребуется решение системы из 5 уравнений, в каждом из которых будет по 5 неизвестных величин и так далее. Да и нагрузка на многопролетную балку далеко не всегда бывает равномерно распределенной, а значит и с определением расчетных характеристик для балки - основной системы также придется повозиться.
В связи с этим для расчетов балок с большой степенью статической неопределимости используется другой метод, который можно назвать методом моментов. | 
