Основные определения
Сопротивление материалов - раздел физики, изучающий механические свойства различных материалов, используемых в строительстве и машиностроении
Сопротивление материалов позволяет определить прочность, жесткость и устойчивость элементов строительных конструкций и деталей машин, тем самым обеспечить долгую и надежную работу сооружений, машин и механизмов.
Объекты рассмотрения - твердые тела
Вещества и комбинации веществ, из которых состоят тела, и являются рассматриваемыми материалами. Все твердые тела по геометрической форме можно условно разделить на 3 группы:
1. Стержни - твердые тела, длина l которых значительно больше высоты h и ширины b.
Это можно выразить соотношением длины к высоте или ширине. Стержни можно условно разделить на 3 категории:
1.1. Стержни с соотношением l/h ≥ 10.
1.2. Стержни с соотношением 5 < l/h < 10.
1.3. Стержни с соотношением l/h ≤ 5. Чем меньше значение соотношения l/h или l/b, тем больше тело по своей геометрической форме приближается к пластине или массивному телу.
2. Пластины - тела, высота которых значительно меньше длины и ширины.
3. Массивные тела - тела, длина, ширина и высота которых сопоставимы.
Примечание: определение длины, ширины и высоты зависит от выбора системы координат. Например и балка перекрытия и колонна могут рассматриваться как стержни, а стена и плита перекрытия - как пластины.
Основной объект рассмотрения - стержень (балка, брус).
Так как высота и ширина стержня значительно меньше длины, то для решения множества задач на начальной стадии высотой и шириной стержня пренебрегают, а для расчетов используют только один параметр - длину стержня. Таким образом на чертежах стержень изображается как линия, имеющая некоторую длину l. Из курса геометрии нам известно, что линия может быть прямой, кривой, находящейся в одной плоскости, и кривой, для корректного описания которой нужно задавать координаты в трех плоскостях. То же можно сказать и о стержнях.
Ось стержня - линия, проходящая через центры тяжести поперечных сечений стержня.
Таким образом линия, изображающая стержень на чертежах, совпадает с осью стержня. Часто ось стержня называется упругой линией, нейтральной линией или нейтральной осью.
Поперечное сечение - сечение стержня в плоскости, перпендикулярной оси стержня.
Основными характеристиками поперечного сечения являются высота и ширина, а так как поперечное сечение перпендикулярно оси стержня, то высота и ширина поперечного сечения являются высотой и шириной стержня в рассматриваемом сечении. При решении некоторых строительных задач рассматриваются не только поперечные, но и наклонные сечения - сечения в плоскости, расположенной под некоторым углом к поперечному сечению или оси стержня. Для получения любого возможного сечения не нужна грубая физическая сила, а только сила мысли и немного пространственного воображения.
Расчет прочности - определение наименьших размеров поперечного сечения элементов конструкции
при которых исключается возможность разрушения конструкции при действии заданных нагрузок. Другими словами напряжения, возникающие в рассматриваемых поперечных сечениях, не должны превышать расчетного сопротивления материала.
Расчет жесткости - определение деформаций материала
возникающих под действием заданных нагрузок. Так как не существует материалов, имеющих бесконечно большую жесткость, то деформации материала конструкции приводят к изменению геометрической формы элементов конструкции, а значит и к перераспределению внутренних напряжений.
Устойчивость - состояние элементов конструкции
при котором изменение первоначальной геометрической формы под действием нагрузок и возникающего при этом перераспределения внутренних напряжений не приводит к разрушению конструкции.
Деформация - изменение геометрических размеров и первоначальной формы физического тела при действии сил.
Деформации рассматриваются как перемещение точек, линий и плоскостей.
Линейная деформация - перемещение рассматриваемой точки, линии или поперечного сечения относительно только одной из выбранных осей координат.
Линейная деформация измеряется в единицах длины.
Угловая деформация - перемещение, характеризуемое углом поворота рассматриваемой линии или поперечного сечения
относительно некоторой точки.
Абсолютная деформация - величина линейной деформации
на рассматриваемом участке длины элемента конструкции.
Относительная деформация - отношение абсолютной деформации к длине
рассматриваемого участка.
Пластические (остаточные) деформации - изменения геометрических размеров и формы тела
остающиеся после снятия нагрузки.
Упругие деформации - деформации тела под действием нагрузок, не приводящие к остаточным деформациям после снятия нагрузок
Другими словами остаточные деформации, при упругой деформации равны нулю.
Упругость - свойство материала полностью восстанавливать первоначальную геометрическую форму тела
после снятия нагрузок.
Пластичность - свойство материала накапливать остаточные деформации
Все материалы обладают определенными упругими и пластичными свойствами. Например изготовление профилированного листа из листа металлопроката происходит в результате накопления остаточных деформаций.
Сжатие или растяжение - такое воздействие на материал, при котором силы, действующие на стержень, направлены по оси или параллельно оси стержня.
Если силы направлены по оси, то такой элемент конструкции называют центрально сжатым или центрально растянутым. Если силы приложены на некотором расстоянии от оси, то такой элемент называют внецентренно сжатым или внецентренно растянутым, при этом расстояние от оси до точки приложения силы называется эксцентриситетом е.
Кручение - воздействие на материал пары сил, действующих в плоскости, перпендикулярной к оси стержня
т.е. в плоскости поперечного сечения
Изгиб - воздействие на материал пары сил, направленных в плоскости, проходящей через ось стержня.
т.е. в плоскости, перпендикулярной плоскости поперечного сечения.
Момент - создается любой парой сил, направленных не по одной прямой, а параллельно, а также любой силой, расположенной на некотором расстоянии от рассматриваемого сечения.
Моменты могут быть крутящими и изгибающими. Момент, возникающий при внецентренном растяжении или сжатии, является изгибающим.
Изотропный материал - материал, физико-механические свойства которого постоянны и одинаковы во всех направлениях
К изотропным материалам условно можно отнести металлы, камень, стекло.
Ортотропный материал - материал, физико-механические свойства которого постоянны, но не одинаковы в различных направлениях
Представителем такого материала является древесина.
Анизотропный материал - материал, не имеющий свойств изотропности или ортотропности
Свойства анизотропных материалов не являются предметом рассмотрения теории сопротивления материалов. Между тем не существует природных или искусственных материалов, имеющих идеальную упругость, изотропию или отротропию. Кроме того изготовить конструкцию идеальной геометрической формы практически невозможно. Это означает, что для точных расчетов необходимо учитывать все изменения геометрической формы, а также возможные отклонения от заданных физико-механических свойств. Однако в подавляющем большинстве случаев для обеспечения надежной работы строительной конструкции, машины или механизма достаточно выполнить приближенный (упрощенный) расчет. Выполняется такой расчет на основании следующих допущений.
Основные допущения, принимаемые в теории сопротивления материалов
1. Рассматриваемый материал является изотропным (или ортотропным) и идеально упругим.
2. Деформации материала пропорциональны приложенной нагрузке, не превышающей некоторой предельной величины, т.е рассматриваемые тела являются линейно-деформируемыми.
3. При составлении уравнений равновесия деформациями материала можно пренебречь, так как деформации рассматриваемых элементов значительно меньше геометрических размеров элементов. В данном случае не только значительно меньше длины, но также высоты и ширины.
4. При расчетах допускается использовать принцип независимости действия сил, т.е. упругую деформацию под действием нескольких сил можно рассматривать как сумму упругих деформаций от каждой отдельно взятой силы.
5. Предполагается, что сечения которые были плоскими до приложения нагрузок, остаются плоскими при деформациях материала.
Внешние и внутренние силы
Все силы, действующие на тело, можно условно разделить на внешние и внутренние. Условно потому, что силы тяжести, действующие на каждую частицу тела, находятся как бы внутри тела, а внутренние силы (силы взаимодействия между элементарными частицами вещества) действуют и до того, как к телу приложена какая-либо внешняя сила.
Потому внешние силы, вызывающие деформацию материала, чаще называют нагрузками, а разницу внутренних сил, возникающую при деформации - напряжениями или внутренними усилиями, подобно тому как в электротехнике напряжением называется разница потенциалов
Единицей измерения силы является Ньютон (Н) или килоНьютон (кН). Однако в технической литературе нередко встречается и другая единица - килограмм-сила (кгс) или тонно-сила (тс). Измерение силы в Ньютонах является более правильным. Так как сила есть произведение массы на ускорение, то тело массой в 1 кг создает нагрузку Q = mg = 1·9.81 м/с2 = 9.81 кг·м/с2 = 9.81 Н. Это означает, что при расчетах значения нагрузок вряд ли будут круглыми. И потому пользоваться при расчетах килограмм-силами или тонно-силами удобнее. Считается, что тело массой 1 кг создает нагрузку 1 кгс.
Внешние силы по характеру приложения можно разделить на четыре вида:
1. Объемные - действующие на все точки тела. Измеряются в Н/м3.
2. Плоские (поверхностные) - распределенные на некоторой площади поверхности тела. Измеряются в Н/м2.
3. Линейные (распределенные) - распределенные непрерывно по некоторой длине. Измеряются в Н/м.
Интенсивность нагрузки - это величина распределенной нагрузки, приложенной к единице объема, площади или длины.
Так как при расчетах изначально рассматривается ось стержня, не имеющая высоты и ширины, то объемные и плоские нагрузки часто приводятся к линейной. Это допускается делать без каких-либо поправочных коэффициентов, если интенсивность объемной или плоской нагрузки является постоянной.
4. Точечные (сосредоточенные) - приложенные в одной точке.
В природе точечных нагрузок не существует. Любая нагрузка прикладывается к некоторой площади, но если площадь приложения нагрузки, точнее длина приложения нагрузки после приведения плоской нагрузки к линейной, значительно меньше длины тела, то такую нагрузку можно условно рассматривать, как сосредоточенную в одной точке. Переход от сосредоточенной нагрузки к равномерно распределенной и наоборот осуществляется только с помощью соответствующих коэффициентов.
По времени действия нагрузки делятся на постоянные и временные
Постоянные нагрузки, например, собственный вес конструкции, действуют в течение всего срока службы. Временные нагрузки ограничены по времени действия.
По характеру изменения во времени нагрузки делятся на статические и динамические
Статические нагрузки прикладываются как бы постепенно, поэтому инертные силы, возникающие при движении инертных масс, при расчетах не учитываются. Динамические нагрузки прикладываются очень быстро и потому при расчетах влияние инертных сил необходимо учитывать.
Все вышеприведенные нагрузки рассматриваются как активные.
Напряжение - величина внутренней силы, приложенной к единице площади рассматриваемого сечения
Равнодействующую внутренних сил, действующую на рассматриваемую площадь, называют внутренним усилием.
Примечание: распределенные нагрузки как правило обозначаются литерой "q" вне зависимости от того, объемная, плоская или линейная нагрузка имеется в виду. Сосредоточенная нагрузка часто обозначается литерой "P", однако я предпочитаю обозначать сосредоточенную нагрузку литерой "Q", а литерой "P" - реактивные внутренние усилия, соответственно литерой "p" - реактивные напряжения.
Уравнения равновесия. Метод сечений
Так как рассматриваемое тело должно быть неподвижным в заданной системе координат, то все опоры тела можно заменить на реактивные силы - опорные реакции. Опорные реакции также рассматриваются как внешние силы. При этом для соблюдения равновесия (неподвижности рассматриваемого тела) сумма активных и реактивных сил, действующих на тело относительно любой координатной оси, должна быть равна нулю. На основании этого предположения составляются уравнения равновесия системы.
Кроме того, если рассечь тело в любом месте, то чтобы тело по-прежнему оставалось в состоянии равновесия к полученному сечению нужно приложить некоторую внешнюю силу Q. Значение внешней силы определяется, исходя из условий равновесия. А так как сила действия равна силе противодействия, то считается, что внутренние усилия Р или напряжения р, возникающие в результате действия внешних сил (нагрузок) равны по значению нагрузкам, приложенным в рассматриваемом сечении и направлены в противоположную сторону. Такой метод расчета и называется методом сечений.
Примечание: Для решения статически неопределимых задач одних только уравнений равновесия и уравнения моментов недостаточно.
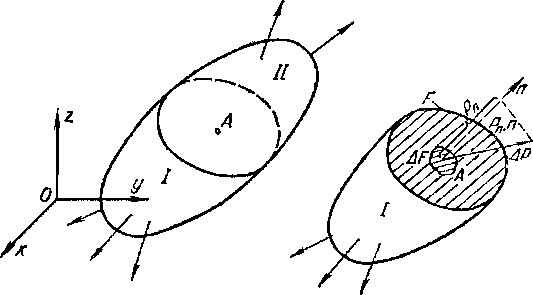
Рисунок 317.1
Так как напряжения, возникающие в рассматриваемых сечениях под действием внешних сил, редко бывают равномерно распределенными (не имеют постоянной интенсивности), то для решения задач сопротивления материалов важно знать не просто значение внутренних усилий, но также и значение напряжений в наиболее опасных точках сечения. Отношение внутреннего усилия ΔР, действующего на некоторой площади ΔF рассматриваемого сечения будет приближаться к некоторому пределу, если площадь ΔF будет стремиться к нулю (к точке А). Этот предел, как мы выяснили ранее, называется напряжением и определяет интенсивность внутренних усилий, действующих на рассматриваемую площадку в точке А. Напряжения могут быть различны не только в разных точках одного сечения, но и в одной и той же точке А, общей для различных сечений, т.е. сечений, рассекающих тело под различными углами.
Ось, перпендикулярная плоскости сечения, называется нормалью.
Полное напряжение в точке А, имеющей координаты (х, у, z) для сечения с нормалью n определяется по формуле:
 (317.1) (317.1)
где ΔР — элементарное внутреннее усилие, возникающее при отбрасывании части II тела и замене этой части элементарной внешней силой ΔQ, действующей на оставшуюся часть I для соблюдения условий равновесия.
Нормальное напряжение σn действует в направлении нормали
Если усилие ΔР не перпендикулярно рассматриваемой плоскости сечения (как на рисунке 317.1), то значение нормального напряжения можно определить по формуле:
 (317.2) (317.2)
Касательное напряжение тn действует в плоскости сечения
Значение касательного напряжения можно определить по формуле:
 (317.3) (317.3)
Напряжения измеряются в Паскалях (Па) или МегаПаскалях (МПа), а также в кгс/см2 или тс/см2.
| 
