1.1. Так как ни один из геометрических параметров, например, ширина шарнирно опертой балки изменяться от b в начале пролета, до 0 в середине пролета не может (такая балка разрушится), то сначала выполняется расчет по прочности и исходя из этого расчета определяются геометрические параметры наиболее нагруженного сечения. Следовательно такую балку можно рассматривать как две балки: одну с постоянной шириной, а вторую с шириной изменяющейся от Δb до 0. При этом эпюра моментов характеризует прогиб для балки постоянного сечения, а кроме того эту эпюру можно рассматривать, как эпюру нормальных напряжений для балки постоянного сечения.
1.2. Общая эпюра нормальных напряжений, возникающих в поперечных сечениях балки, характеризует общий прогиб балки.
1.3 Если наложить эпюру моментов на эпюру напряжений балки переменного сечения, то соблюдении определенных условий разница между этими эпюрами покажет изменение прогиба для балки переменного сечения.
Точнее разность площадей этих эпюр можно рассматривать как некую фиктивную нагрузку и тогда разница этих эпюр покажет изменение фиктивной опорной реакции А, а при делении полученного значения на жесткость - изменение угла поворота на опоре А. Тогда фиктивный момент (фиктивная опорная реакция, умноженная на расстояние от точки приложения фиктивной опорной реакции до рассматриваемой точки, минус площадь разностной эпюры, умноженная на расстояние от центра тяжести разностной эпюры до рассматриваемой точки) покажет изменение прогиба.
Примечание: принципы графоаналитического метода в данной статье на рассматриваются.
Например, для балки с линейно изменяющейся шириной b разностная эпюра будет выглядеть так:
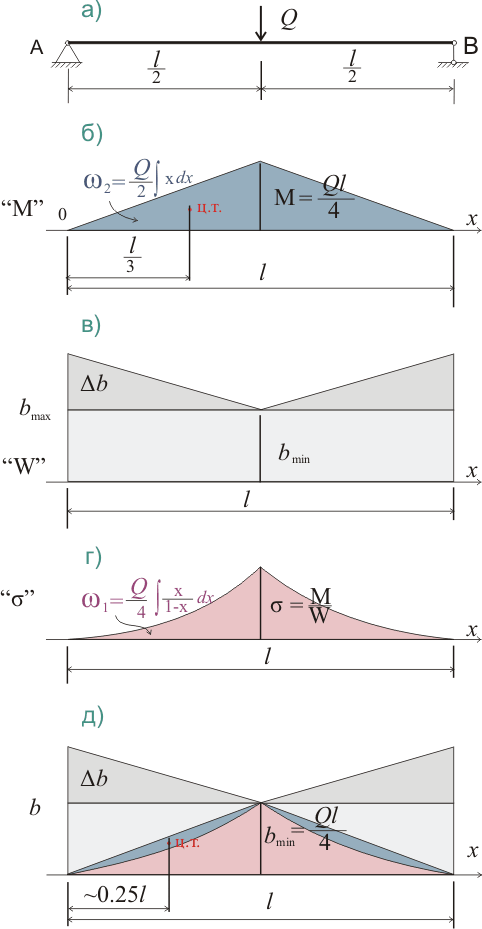
Рисунок 323.1.1
При этом на разностную эпюру будет влиять не только характер нагрузки на балку, но также и величина отклонения от минимально допустимого размера поперечного сечения. Так, если Δb → 0, то сечение балки стремится к постоянному значению. При значительном увеличении Δb по сравнению с b уменьшается эффективность использования материала, хотя при этом и прогиб уменьшается. Условие Δb → b не допускается принятыми в п.1.1 ограничениями. Поэтому расчет балок с сечением, уменьшающимся от начала балки к середине, зависит от значения bmin. Кроме того, от значений bmin и Δb зависит характер изменения нормальных напряжений.
Прогиб балки с линейно уменьшающейся шириной сечения при сосредоточенной нагрузке посредине пролета
1.4. Так как изменение нормальных напряжений для балки с сосредоточенной нагрузкой описывается зависимостью вида:
σ = М/W = 6Ax/bh2 (323.1.1)
то при постоянном значении h2/6 = C = 1 формула (323.1.1) примет вид:
σ = Qx/2C(b - bminy) = Qx/2(nbmin - bminy) (323.1.2)
После соответствующих преобразований получим следующую зависимость:
bminσ = Qx/2(n - y) (323.1.3)
Где bmin в данном случае постоянная величина и ее значение также можно принять равным 1. Тогда например, при Δb = bmin = b/2, n = 2, у = 2х, разностная эпюра описывается двумя линиями, имеющими следующую зависимость:
f1(x) =σп = Qx/2; f2(x) = σи = Qx/4(1- x) (323.2.1)
В данном случае значение опорной реакции А = Q/2 - постоянная величина и для упрощения расчетов ее можно вынести за пределы интегрирования. Данные линии пересекаются в точках 0 и 0.5 (начало балки и середина пролета или нижний и верхний предел интегрирования), тогда:
ω2 = (Q/2)∫хdx = (Q/2)(x2/2) = (Q/2)(l2/8) = Ql2/16 (323.2.2)
ω1 = (Q/2)(1/2)∫(x/(1-x))dх = (Q/4)(-x - ln(1 - x)) = (Q/4)(0.193147)l2 = 0.772588Ql2/16 (323.2.3)
тогда площадь разностной эпюры составит:
ωр = ω2 - ω1 = Ql2/16 - 0.77288Ql2/16 = 0.22712Ql2/16 (323.2.4)
Примечание: В данном случае нас интересует разностная эпюра потому, что определить расстояние до центра тяжести разностной эпюры намного проще, чем искать центр тяжести для эпюры с площадью ω1. Визуально (рис.323.1 д) это расстояние составляет l/4. Кроме того для визуальной оценки результатов интегрирования для эпюр моментов и напряжений на рисунках 323.1 - 323.3 сначала строились графики функций (см. рис.323.1.2).
Значение фиктивного изгибающего момента составит:
Mф = Ql2/16(l/3) - (0.22712Ql2/16)(l/4) = Ql3/48 - 0.17Ql3/48 = 0.83Ql3/48 (323.2.5)
fпр = 0.83Ql3/48EIbmin (323.2.6)
В данной случае Ibmin означает, что мы рассматриваем изменение прогиба по отношению к балке с постоянным моментом инерции и соответственно постоянной шириной сечения bmin.
Чтобы было еще более наглядно, для рассматриваемого случая увеличение материала балки в 1.5 раза приводит к уменьшению прогиба в 1.184 раза.
Если изменение ширины сечения будет описываться другой зависимостью, то приближенные результаты можно получить интерполяцией данных рисунка 323.1.2.
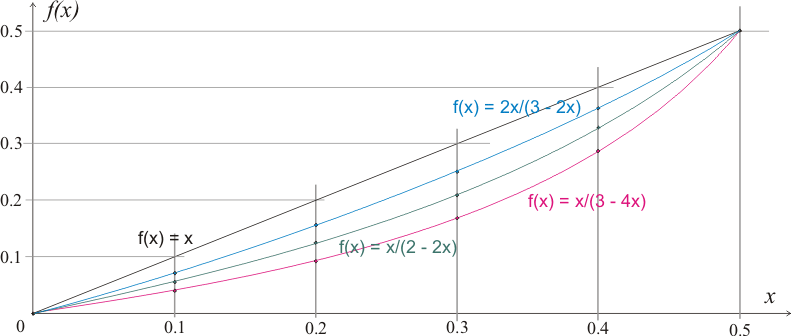
Рисунок 323.1.2
Как видно из данного рисунка, при соотношении Δb/b = 1/3 (f(x) = 2x/(3 - 2x)) площадь разностной эпюры будет приблизительно в 2 раза меньше, чем при рассматривавшемся соотношении 1/2. При соотношении 2/3 площадь разностной эпюры увеличится приблизительно на 1/2.
Прогиб балки с линейно уменьшающейся шириной сечения при равномерно распределенной нагрузке
При равномерно распределенной нагрузке изменится и эпюра моментов и эпюра нормальных напряжений
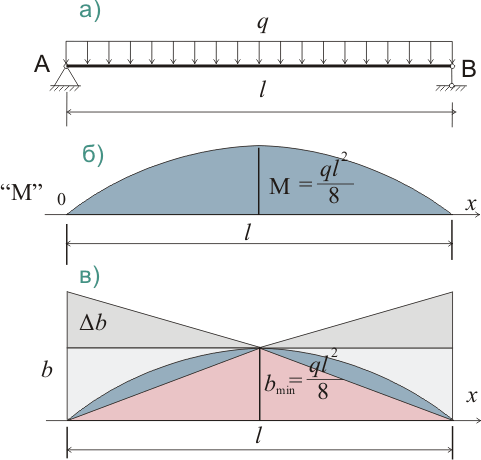
Рисунок 323.2
σ = М/W = 6(qlx - qx2)/2bh2 (323.4.1)
то при постоянном значении h2/3 = C =1 формула 323.1.1) примет вид:
σ = (qlx - qx2)/C(nbmin - bminy) (323.4.2)
bminσ = (qlx -x2)/(n - y) (323.4.3)
При bmin ;= 1, при Δb = bmin = b/2, n = 2, у = 2х, разностная эпюра описывается двумя линиями, имеющими следующую зависимость:
f1(x) = (qlx - qx2); f2(x) = (qlx - qx2)/2(1- x) (323.4.4.1)
Данные линии пересекаются в точках 0 и 0.5 (начало балки и середина пролета или нижний и верхний предел интегрирования), тогда:
ω2 = q∫(lх - x2)dx = q(l∫xdx - ∫x2dx) = q(l3/8 - l3/24) = ql3/24 (323.4.5.1)
ω1 = (q/2)(l∫x/(1-x) - ∫(x2/(1-x))dх = (ql/2)(0.193147)l2 - (q/2)(0.068147)l3 = ql3/32 (323.4.6.1)
тогда площадь разностной эпюры составит:
ωр = ω2 - ω1 = ql3/24 - ql3/32 = ql3/96 = 0.25ql3/24 (323.4.7)
Тогда значение фиктивного изгибающего момента составит:
Mф = ql3/24(5l/16) - (ql3/96)(l/4) = 5ql4/384 - ql4/384 = ql4/96 = 4ql4/384 (323.4.8)
fпр = 4ql4/384EIbmin (323.4.9)
В данной случае Ibmin также означает, что мы рассматриваем изменение прогиба по отношению к балке с постоянным моментом инерции и соответственно постоянной шириной сечения bmin.
Чтобы было еще более наглядно, при равномерно распределенной нагрузке увеличение материала балки в 1.5 раза приводит к уменьшению прогиба в 1.2 раза.
Если длину балки также принять за некую единицу, что допустимо при выбранных нами пределах интегрирования, то уравнения функций будут выглядеть так:
f1(x) = (q/2)x(1 - x); f2(x) = (q/4)x(1 - x)/(1- x) = qx/4 (323.4.4.2)
Т.е. в данном случае график, описывающий эпюру напряжений, имеет линейную зависимость (рис.323.2 в).
ω2 = (q/2)∫x(1 - x)dx = (q/2)(1/12) = q/24 = ql3/24 (323.4.5.2)
ω1 = (q/4)∫xdх = (q/4)(x2/2) = (q/4)(1/8) = ql3/32 (323.4.6.2)
Прогиб балки с линейно уменьшающейся высотой при сосредоточенной нагрузке посредине балки
Так как момент сопротивления W = bh2/6 для прямоугольного сечения, то даже при линейно уменьшающейся высоте зависимость между нормальными напряжениями и эпюрой моментов будет не линейной даже при сосредоточенной нагрузке, приложенной посредине балки. При равномерно распределенной нагрузке определение прогиба методом интегрирования еще более усложнится. Но в целом влияние изменения высоты на прогиб изменится, так как в данном случае следует рассматривать не изменяющуюся высоту, а квадрат изменяющейся высоты, а так как момент инерции это I = bh3/12 для прямоугольного сечения, то эпюру моментов следует сравнивать с кубическим изменением высоты сечения.
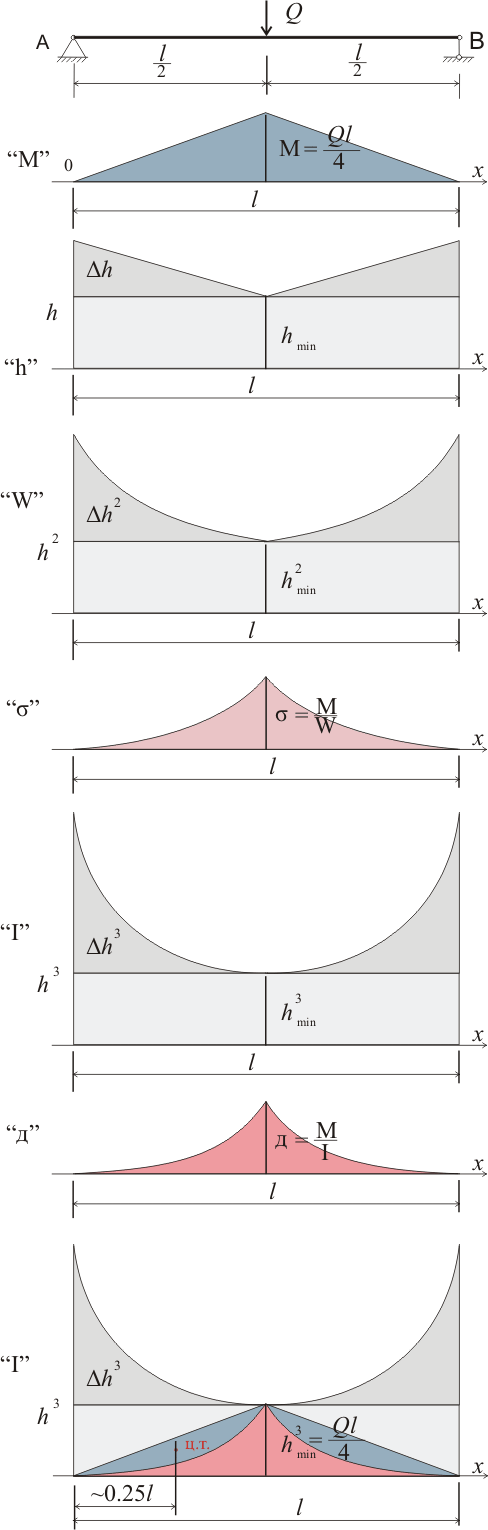
Рисунок 323.3
При Δh = hmin = h/2, n = 2, у = 2х, разностная эпюра описывается двумя линиями, имеющими следующую зависимость:
f1(x) = Qx/2; f2(x) = Qx/16(1- x)3 (323.5.1)
ω2 = (Q/2)∫хdx = (Q/2)(x2/2) = (Q/2)(l2/8) = Ql2/16 (323.5.2)
ω1 = (Q/2)(1/8)∫(x/(1-x)3)dх = (Q/16)(1/2) = Ql2/32 (323.5.3)
тогда площадь разностной эпюры составит:
ωр = ω2 - ω1 = Ql2/16 - Ql2/32 = Ql2/32 (323.5.4)
Значение фиктивного изгибающего момента составит:
Mф = Ql2/16(l/3) - Ql2/32(l/4) = Ql3/48 - Ql3/128 = (1 - 0.375)Ql3/48 = 0.625Ql3/48 (323.5.5)
fпр = 0.625Ql3/48EIbmin (323.5.6)
Примечание: расстояние от центра тяжести разностной эпюры до начала координат определено визуально по рисунку 323.3.
Прогиб балки с линейно уменьшающейся высотой сечения при равномерно распределенной нагрузке
Так как при линейно уменьшающейся ширине сечения разница в прогибах при сосредоточенной нагрузке, приложенной посредине пролета и равномерно распределенной нагрузке крайне незначительна, то можно предположить, что такая же незначительная разница будет и при линейно изменяющейся высоте сечения. Тогда при Δh = hmin = h/2
fпр ≈ 3ql4/384EIbmin (323.6.6)
Прогиб балки с высотой сечения, уменьшающейся пропорционально изгибающему моменту
Примером такой балки является любая шарнирно опертая железобетонная балка с трещинами в растянутой зоне. В результате действия нормальных напряжений высота сжатой зоны сечения балки изменяется нелинейно. Эту зависимость можно приблизительно выразить так:
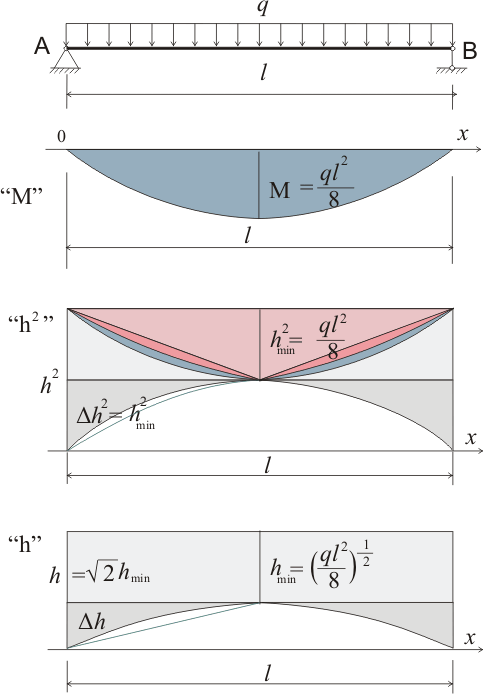
Рисунок 323.4
Железобетонная балка с арматурой в растянутой зоне может рассматриваться как балка переменного сечения. В поперечных сечениях, в которых изгибающий момент равен нулю или очень мал, сжимающие напряжения вызывают упругие деформации бетона, растягивающие напряжения вызывают упругие деформации и бетона и арматуры. При выбранной расчетной схеме сжимаемой будет верхняя часть сечения, а растягиваемой нижняя часть сечения. После того, как растягивающие напряжения достигнут предела прочности бетона при растяжении, бетон в растягиваемой зоне начнет разрушаться - начнут образовываться трещины - и потому с увеличением растягивающих напряжений все большую часть этих напряжений будет воспринимать арматура и все меньшую часть бетон нижней части сечения. Таким образом будет уменьшаться высота приведенного сечения балки. Минимальной высота приведенного сечения будет в точке действия максимального изгибающего момента.
При этом увеличение изгибающего момента будет приводить к уменьшению квадрата высоты сжатой зоны сечения (эпюра "h2"). На эпюре "h2" также показано влияние нелинейного изменения высоты сечения по сравнению с линейным изменением высоты сечения. При подобном нелинейном изменении высоты площадь разностной эпюры при соотношении hmin = h/2 будет в 2 раза меньше, чем при линейном изменении высоты.
Если рассматривать только упругие деформации сжатой области поперечных сечений бетона, то уменьшение квадрата высоты в два раза означает изменение высоты Δh от 0 до hmin/√2.
Таким образом, используя данные, полученные при рассмотрении балок с линейно уменьшающейся шириной и высотой сечения, суммарное влияние нелинейного изменения высоты и изменения соотношения hmin/h можно выразить так:
fпр ≈ 5ql4/384EIhmin - 2ql4/(384·2·1.41EIhmin) = (5 - 0.7)ql4/384EIhmin ≈ 4.3ql4/384EIhmin ≈ 0.86·5ql4/384EIhmin (323.7.6.1)
При этом 0.86 можно рассматривать как значение поправочного коэффициента, учитывающего изменяющуюся высоту балки.
Примечание: Более точное определение влияния изменяющейся высоты сжатой зоны сечения на прогиб является достаточно трудоемкой задачей, в частности следует учесть что высота сечения начнет изменяться не сразу от начала балки, так как возле опор при данной расчетной схеме будут участки без трещин. Но даже если в ходе логических рассуждений были допущены ошибки, то все равно точное значение коэффициента не может выходить за пределы 0.8-0.9, потому для оценочных расчетов прогиба железобетонных балок при равномерно распределенных нагрузках можно использовать указанное в формуле (323.7.6) значение. Впрочем, на определение прогиба железобетонных балок куда большее влияние могут оказать пластические деформации в сжатой зоне бетона и как следствие - уменьшение начального модуля упругости бетона на некотором участке длины балки, что можно рассматривать и как дополнительное уменьшение высоты сечения.
Соответственно, если по каким-либо причинам изменение высоты сечения составит h/2, то
fпр ≈ 5ql4/384EIhmin - 2ql4/(384·2·EIhmin) = (5 - 1)ql4/384EIhmin ≈ 4ql4/384EIhmin ≈ 0.8·5ql4/384EIhmin (323.7.6.2)
Если изменение высот будет от 0 до hmin/2√2, то
fпр ≈ 5ql4/384EIhmin - 2ql4/(384·2·2·1.41EIhmin) = (5 - 0.35)ql4/384EIhmin ≈ 4.65ql4/384EIhmin ≈ 0.93·5ql4/384EIhmin (323.7.6.3) | 
