Модуль упругости бетона

При расчетах бетонных и железобетонных конструкций по второй группе предельных состояний, в частности при определении прогибов, необходимо знать модуль упругости E (модуль Юнга) бетона при сжатии. При этом следует различать начальный E_b и приведенный E_b1 модули упругости.

Факторы, влияющие на значение расчетного модуля упругости

Более подробно сущность модуля упругости, предела пропорциональности, предела прочности, нормальных напряжений, деформаций и других понятий рассматривается отдельно. Здесь лишь отметим, что для материалов, у которых предел пропорциональности незначительно меньше предела текучести, можно использовать линейную деформационную модель. Т.е. предполагать деформации прямо пропорциональными нормальным напряжениям.

Примером таких материалов являются стали различных марок. А вот бетон к таким материалам не относится. Более того, у бетона нет ярко выраженного предела пропорциональности и предела текучести. Диаграмма напряжений бетона при постепенном загружении выглядит приблизительно так:

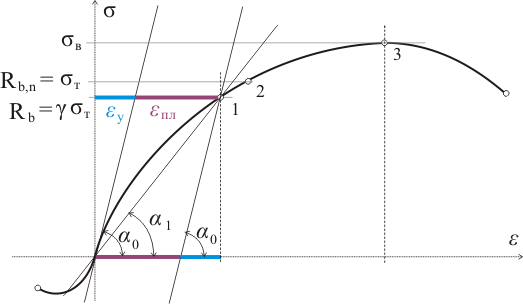
Рисунок 324.1

Однако это далеко не единственная из возможных диаграмм напряжений бетона, так как на значение деформаций ε будут влиять не только нормальные напряжения σ, возникающие в поперечных сечениях, но и множество других факторов:

1. Класс бетона

Начальный модуль упругости бетона зависит от класса бетона. Значение начального модуля упругости можно определить по следующей таблице:

Таблица 1. Начальные модули упругости бетона (согласно СП 52-101-2003)

2. Время приложения нагрузки

При кратковременном действии нагрузки деформации бетона почти прямо пропорциональны напряжениям, кроме того такие деформации остаются упругими. При расчетах на кратковременное действие нагрузки (до 1-2 часов) значение приведенного модуля упругости на участках без трещин определяется по формуле:

E_bп = φ_b1E_b (324.1)

где φ_b1 = 0.85 - для тяжелых, мелкозернистых и легких бетонов на плотном мелком заполнителе; = 0.7 - для поризованных и легких бетонов на пористом мелком заполнителе.

При длительном действии нагрузки того же значения, деформации начинают увеличиваться до некоторого предела, например при σ = R_b - до точки 1 на диаграмме напряжений. После снятия нагрузки пластические деформации ε_пл останутся (потому они пластическими и называются), а при повторном загружении до указанного предела деформации будут прямо пропорциональны напряжениям. Процесс нарастания пластических деформаций с течением времени при постоянных нормальных напряжениях называется ползучестью бетона.

Так как при длительном действии нагрузки диаграмма напряжений стремится к показанной на рисунке 324.1, то при расчетах необходимо учитывать нелинейность изменения деформаций при линейно изменяющихся напряжениях. К тому же в изгибаемых элементах нелинейному изменению деформаций препятствует сам материал. Напомню, нормальные напряжения в поперечных сечениях изгибаемых элементов прямо пропорциональны расстоянию от центра тяжести сечения, через который проходит нейтральная линия, до рассматриваемой точки. Таким образом различные слои бетона, работающие совместно, приводят к частичному перераспределению деформаций по высоте элемента, при этом перераспределенную эпюру деформаций можно условно рассматривать как линейную:

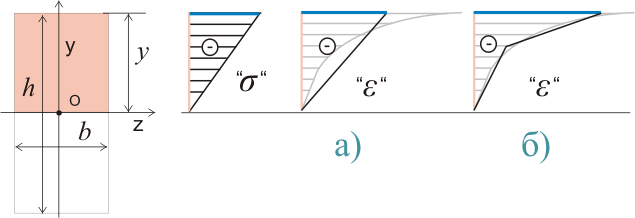
Рисунок 324.2

На рисунке 324.2 показана некоторая высота сжатой зоны сечения у, при которой нормальные напряжения σ будут прямо пропорциональны расстоянию от центра тяжести до рассматриваемой точки, это соответствует работе бетона в области условно упругих деформаций. При этом изменение деформаций можно рассматривать по зависимости, показанной на рисунке 324.2.а) или 324.2.б). Часто расчетами на прочность допускается наличие в сжатой области пластического шарнира, при котором изменяется эпюра напряжений и соответственно увеличивается значение деформаций:

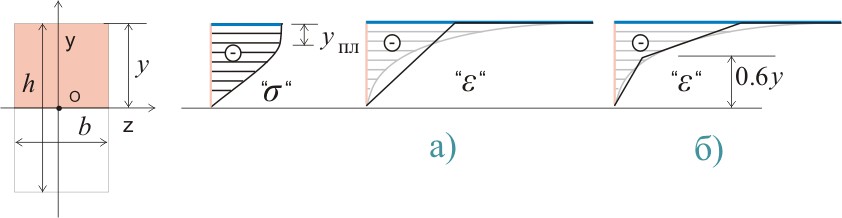
Рисунок 324.3

На основании этого для упрощения расчетов обычно принимается двухлинейная (рис. 324.3. а) или трехлинейная (рис. 324.3.б) диаграмма состояния сжатого бетона. Согласно СП 52.101.2003 трехлинейная диаграмма выглядит так:

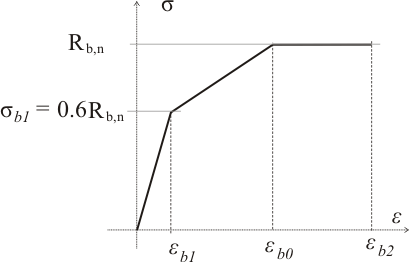
Рисунок 324.4

где

ε_b1 = 0.6R_b,n/E_b1 (324.2)

Е_b1 - при кратковременном действии нагрузки принимается равным E_b, а при длительном действии нагрузки определяется по следующей формуле:

E_b1 = E_b/(1 + φ_b,cr) (324.3)

где φ_b,cr - коэффициент ползучести бетона, определяемый в зависимости от класса бетона и влажности окружающей среды. Таким образом учитывается третий фактор, влияющий на модуль упругости бетона:

3. Влажность воздуха

Значение коэффициента ползучести определяется по следующей таблице:

Таблица 2. Коэффициенты ползучести бетона

а значения деформаций ε_bo и ε_b2 при необходимости (если нормальные напряжения больше 0.6Rb,n) определяются по таблице 3:

Таблица 3. Относительные деформации бетона (согласно СП 52-101.2003)

4. На значение модуля упругости бетона также влияют температура окружающей среды и интенсивность радиоактивного излучения.

Значение начальных модулей упругости, приведенных в таблице 1, соответствует температуре окружающей среды +20±5^оС и нормальному радиационному фону. При изменении температуры в пределах ±20 от указанного значения влияние температуры на модуль упругости можно не учитывать. А при больших изменениях температуры следует учитывать еще и температурные деформации бетона. В целом уменьшение температуры приводит к увеличению модуля упругости, но и к повышению хрупкости материала, а увеличение температуры - к уменьшению модуля упругости и к увеличению пластичности материала.

А теперь попробуем выяснить, как все эти теоретические цифры можно применить на практике.

Определение значения модуля упругости

Имеется железобетонная прямоугольная плита перекрытия - шарнирно опертая бесконсольная балка размерами h = 20 см, b = 100 см; ho = 17.3 см; пролетом l = 5,6 м; бетон класса В15 (начальный модуль упругости Е_b = 245000 кгс/см²; R_b,ser (R_b,n) = 112 кгс/см², R_b = 85 кгс/см²); растянутая арматура класса А400 (E_s= 2·10⁶ кгс/см²) с площадью поперечного сечения A_s = 7.69 cм² (5 Ø14); полная равномерно распределенная нагрузка q = 7,0 кг/см, сумма постоянных и длительных нагрузок q_l = 6.5 кгс/см

1. Сначала выясним, какими будут параметры сечения при расчетном модуле упругости Е_b1. Согласно формулы (324.3) и таблицы 2, при классе бетона В15 и при влажности 40-75%:

E_b1 = 245000/(1 + 3.4) = 55681 кгс/см²

2. Тогда высоту сжатой части приведенного сечения посредине балки можно найти, решив следующее уравнение:

у³ = 3A_s(ho - y)²E_s/bE_b1 (321.2.4)

Решение этого уравнения для рассматриваемой плиты даст у_l/2 = 8.61 см.

Тогда приведенный момент сопротивления при такой высоте сжатой зоны сечения составит:

W = 2by²/3 = 2·100·8.61²/3 = 4942.14 см³

3. Определим значение максимальных нормальных напряжений. Так как увеличение деформаций следует учитывать только при действии постоянных и длительных нагрузок, то значение момента от таких нагрузок составит:

σ = M/W = q_ll²/8W = 6.5·560²/(8·4942.14) = 51.56 кгс/см² < 0.6R_b,n = 0.6·112 = 67.2 кгс/см² (321.3.1)

Это означает, что для дальнейших расчетов плиты на действие длительных нагрузок можно использовать полученное значение модуля упругости бетона без каких-либо дополнительных поправок.

4. Расчетный момент инерции составит

I_p = W·y = 4942.14·8.61 = 42551.8 см⁴ (321.5)

5. Значение прогиба при действии постоянных и длительных нагрузок составит

f = k5ql⁴/384E_b1I_p = 0.93·5·6.5·560⁴/(384·55681·42551.8) = 3.27 см (321.6)

где k = 0.93 - коэффициент, учитывающий изменение высоты сжатой зоны поперечного сечения по длине балки. На первый взгляд это кажется странным, ведь когда мы определяли прогиб по начальному модулю упругости бетона и использовали коэффициент k = 0.86, то пригиб составлял 3.065 см, т.е. при использовании коэффициента k = 0.93 прогиб был бы даже больше и составлял 3.31 см. Однако ничего странного в этом нет. Объясню, почему.

При определении прогиба по начальному модулю упругости мы искусственно занизили значение высоты сжатой зоны из-за нарастания пластических деформаций в результате превышения расчетного сопротивления. В данном же случае уменьшение модуля упругости бетона означает увеличение высоты сжатой зоны, а кроме того, значение нормальных напряжений, как показал расчет, не превышает 0.6R_b,n.

В связи с этим разницу при определении приблизительного прогиба по начальному и расчетному модулям упругости бетона можно считать не существенной. Т.е. при определении приблизительного значения прогиба расчет можно выполнять как по начальному значению модуля упругости бетона, так и с учетом его изменения в результате действия длительной нагрузки. Вот в в принципе и все.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

На главную

• Расчет конструкций ::: Расчет железобетонных конструкций

Комментариев нет

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).