Например для двухпролетной бесконсольной балки с равными пролетами, на которую действует равномерно распределенная нагрузка, все основные расчетные данные уже давно определены. Достаточно в имеющиеся формулы подставить значения длины пролета и действующей нагрузки. В целом эпюра моментов для двухпролетной бесконсольной балки будет выглядеть так:
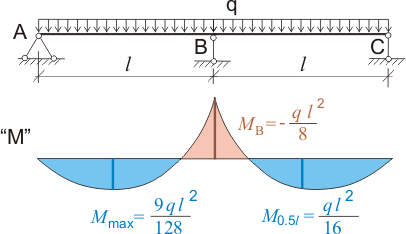
Рисунок 346.1. Эпюра моментов для двухпролетной балки с равными пролетами при действии равномерно распределенной нагрузки.
При этом
МА = МС = 0 (1.1)
МВ = - ql2/8 (1.2)
A = C = 3ql/8 (1.3)
B = 10ql/8 (1.4)
Соотношение опорных реакций В/А = 10/3 = 3.33.
Между тем, если добавить к бесконсольной балке консоли и к этим консолям приложить такую же равномерно распределенную нагрузку, как и в пролетах, то эпюра изгибающих моментов изменит свой вид, да и значения опорных реакций изменятся. Как, мы сейчас и выясним.
Если двухпролетная балка имеет консоли длиной k, то в результате действия нагрузки на одну консоль возле опоры А будет действовать изгибающий момент:
МА = - qk2/2 (2.1)
В данном случае знак "-" означает, что растягивающие напряжения будут действовать в верхней части поперечных сечений балки на опоре. А еще в результате действия нагрузки на консоль будет возникать изгибающий момент и на опоре В.
Если нагрузка будет действовать только на одну из консолей, то согласно закономерностей, определенных при расчете балок методом моментов, значение момента на опоре В будет с обратным знаком и в 4 раза меньше значения момента на опоре А (если балка 1 раз статически неопределимая). Т.е. момент на опоре В будет равен:
МВ = qk2/8 (2.2)
А момент на опоре С будет равен нулю. Теперь нам ничто не мешает определить опорные реакции. Чтобы создать момент на опоре В, равный указанному, опорная реакция С должна быть равна:
С = МВ/l = qk2/8l (2.3)
тогда, чтобы получить на опоре А момент, равный указанному, исходя из уравнения моментов:
С2l + Bl = qk2/4 + Bl = - qk2/2 (2.4.1)
B = (- qk2/2 - qk2/4)/l = -3qk2/4l (2.4.2)
Тогда реакция на опоре А, исходя из условий равновесия системы:
А + В + С = qk (2.5.1)
A = qk - B - C = qk + 3qk2/4l - qk2/8l = qk + 5qk2/8l (2.5.2)
При этом эпюра моментов будет выглядеть так:
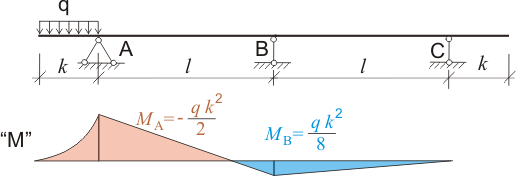
Рисунок 346.2. Эпюра моментов для двухпролетной балки с одной загруженной консолью.
Проверим, не ошиблись ли мы где-нибудь в расчетах. Если составить уравнение моментов для крайнего левого сечения, то суммарный момент в этом сечении должен быть равен нулю. Для простоты расчетов примем значение k = l. Тогда
C3l - B2l + Al - ql2/2 = 3(ql2/8) - 2(6ql2/8) + 13ql2/8 - 4ql2/8 = 0 (2.6)
Тогда, если равномерно распределенная нагрузка действует на обе консоли, то
МА = МС = - qk2/2 (3.1)
МВ = 2qk2/8 = qk2/4 (3.2)
A = C = qk + qk2/8l + 5qk2/8l = qk + 3qk2/4l (3.3)
B = 2(- 3qk2/4l) = -3qk2/2l (3.4)
При этом эпюра моментов для балки, у которой загружены обе консоли, будет выглядеть так:
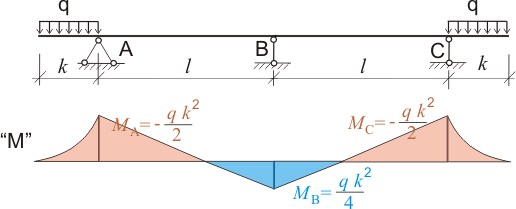
Рисунок 346.3. Эпюра моментов для двухпролетной балки с двумя загруженными консолями.
Если у консолей балки есть некоторая вполне определенная длина, например, k = l/4, тогда для двухпролетной шарнирно опертой балки с двумя консолями, на которые действует равномерно распределенная нагрузка:
МА = МС = - ql2/(2·42) = - ql2/32 (4.1)
МВ = ql2/(4·42) = ql2/64 (4.2)
A = C = ql/4 + 3ql2/64l = 19ql/64 (4.3)
B = - 3ql2/32l = - 3ql/32 (4.4)
Соответственно, если равномерно распределенная нагрузка действует по всей длине балки, включая консоли, то
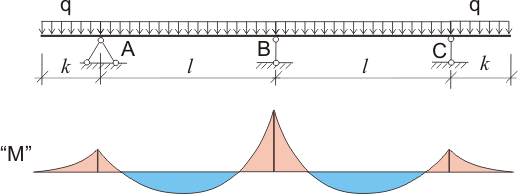
Рисунок 346.4. Суммарная эпюра моментов для балки с консолями загруженной по всей длине.
МА = МС = - ql2/(2·42) = - ql2/32 (5.1)
МВ = - ql2/8 + ql2/64 = - 7ql2/64 (5.2)
A = C = 3ql/8 + 19ql/64 = 43ql/64 (5.3)
B = 10ql/8 - 3ql/32 = 37ql/32 (5.4)
Соотношение опорных реакций в этом случае составляет В/А = 37·2/43 = 1.721.
Если длина консолей балки будет составлять k = l/3, тогда для двухпролетной шарнирно опертой балки с двумя консолями, на которые действует равномерно распределенная нагрузка:
МА = МС = - ql2/(2·32) = - ql2/18 (4.1)
МВ = ql2/(4·32) = ql2/36 (4.2)
A = C = ql/3 + 3ql2/36l = 16ql/36 (4.3)
B = - 3ql2/32l = - 3ql/18 (4.4)
Соответственно, если равномерно распределенная нагрузка действует по всей длине балки, включая консоли, то
МА = МС = - ql2/(2·42) = - ql2/18 (5.1)
МВ = - ql2/8 + ql2/36 = - 7ql2/36 (5.2)
A = C = 3ql/8 + 16ql/36 = 59ql/72 (5.3)
B = 10ql/8 - 3ql/18 = 78ql/72 (5.4)
Соотношение опорных реакций в этом случае составляет В/А = 78/59 = 1.322
Таким образом действие нагрузки на консоли балки приводит к появлению изгибающих моментов на опорах А и С и к уменьшению изгибающего момента на опоре В. Кроме того уменьшается разница между значениями опорных реакций. На основании полученных данных мы можем даже построить график, отражающий изменение соотношения В/А при изменении длины консоли:

Рисунок 346.5. График, отражающий изменение соотношения опорных реакций при изменении длины консоли.
А теперь несколько слов о том, зачем еще эти формулы могут понадобиться.
Например, вы рассчитываете сплошную фундаментную плиту, которая может рассматриваться как балка, у которой нагрузки от стен - это опорные реакции, а давление, оказываемое плитой на основание - это распределенная нагрузка. Так вот, если на плиту опираются 3 стены (2 наружных и одна внутренняя), то нагрузки от стен очень редко пропорциональны опорным реакциям для двухпролетной балки. Так как в реальности опоры балки могут перемещаться относительно вертикальной оси, проще говоря, фундамент будет проседать, то такое несоответствие между нагрузками от стен и опорными реакциями для балки будет приводить к тому, что плита просядет не равномерно.
Кроме того, поперечные сечения бесшарнирной балки на крайних опорах будут иметь некоторый угол наклона по отношению к горизонтальной оси. Это означает, что стены будут отклоняться от вертикали, что может привести к трещинам в стенах из натурального или искусственного камня, если не будут приняты соответствующие меры по усилению стен. Другими словами в стенах будут возникать горизонтальные растягивающие напряжения. А если нагрузка от внутренней стены будет меньше требуемой по расчету, то это приведет к дополнительному увеличению угла наклона на крайних опорах, а значит и к увеличению горизонтальных растягивающих напряжений. Кстати сказать, это относится и к сплошным фундаментным плитам, рассматриваемым как однопролетные балки.
В принципе определить прогиб или угол поворота - не проблема. Как известно, чем больше жесткость балки - тем меньше прогиб и угол поворота, однако это означает, что минимизация прогиба или угла поворота выльется в дополнительную толщину сплошной фундаментной плиты - бесконсольной балки, а устройство консолей соответствующей длины позволяет минимизировать угол поворота плиты на крайних опорах и неравномерность проседания фундамента.
Расчет балки с разными по длине пролетами и консолями
Ну а если балка имеет неравные по длине пролеты и консоли, то формулы значительно усложнятся (первая консоль обозначается ниже как а, первый пролет - b, второй пролет - с, вторая консоль - d, расчет выполняется на основе расчета двухпролетной бесконсольной балки с разными пролетами и двухпролетной балки с одной консолью) и будут выглядеть так:
1. Сначала определяется момент на опоре С:
MС = -qd2/2
2. Затем дополнительный момент на опоре В:
MBд = -MCb/(2(a + b)) = qbd2/(4(a + b))
3. В итоге момент на опоре В:
MВ = - q(a3 + b3)/8L + q(aс2 + bd2)/(4(a + b))
4. Дополнительные опорные реакции:
RCд = qd - МC/b + MBд/b = qd + qd2/2b + qd2/(4(a + b))
RAд = MВд/a = qbd2/(4a(a + b))
RBд = МC/b - MBд/b - MBд/а = -qd2/2b - qd2/(4(a + b)) - qbd2/(4a(a + b))
5 Проверка:
RA + RB + RC - qd = qd + qd2/2b + qd2/(4(a + b)) + qbd2/(4a(a + b)) = - qd2/2b - qd2/(4(a + b)) - qbd2/(4a(a + b))= qd- qd = 0
6. Итоговые опорные реакции:
RA = q(а/2 - (a3 + b3)/8La + c + с2/2a + с2/(4(a + b)) + bd2/(4a(a + b)))
RC = q(b/2 - (a3 + b3)/8Lb + ас2/(4b(a + b)) + d + d2/2b + d2/(4(a + b)))
RB = qL/2 + q(a3 + b3)/8La + q(a3 + b3)/8Lb - qс2/2a - qс2/(4(a + b)) - qас2/(4b(a + b)) - qd2/2b - qd2/(4(a + b)) - qbd2/(4a(a + b))
7. Для определения максимального изгибающего момента в первом пролете а сначала определяется точка, где касательные напряжения равны 0:
"Q"х = RA - qx = 0
x = RA/q
M1пр = RA(х - с) - qx2/2
8. Для определения максимального изгибающего момента во втором пролете b сначала определяется точка, где касательные напряжения равны 0:
"Q"х = RC - qx = 0
x = RC/q
M2пр = RC(x - d) - qx2/2
Примечание: в данном случае значение х будет определяться не от начала, а от конца балки.
9. Для определения максимального прогиба в первом пролете а сначала определяется точка, где угол наклона поперечного сечения равен 0. Для этого сначала определяется угол наклона поперечного сечения в начале балки:
fB = - θн(a + c) + RAa3/6EI - q(a + с)4/24EI + qc4/24EI + θнc = 0
θн(a + с - c) = RAa3/6EI - q((a + с)4 - c4)/24EI
θн = (4RAa3/6EI - q((a + с)4 - c4))/(24EIa) = (4RAa2 - q((a + с)4 - c4)/a)/24EI
тогда:
- Θн + RA(х - с)2/2EI - qx3/6EI = 0
10. Кубическое уравнение будет иметь вид:
qx3/6EI - RA(х - с)2/2EI + Θн = 0
Далее:
fпр = qc4/24EI + θн(c - х) + RA(х - с)3/6EI - qx4/24EI =
(qc4 + (4RAa2 - q((a + с)4 - c4)/a)(c - х) + 4RA(х - с)3 - qx4)/24EI
11. Проверка:
При х = c
fA = (qc4 + (4RAa2 - q((c + a)4 - qc4)/a)(c - c) + 4RA(a - a)3 - qc4)/24EI = (qc4 - qc4)/24EI = 0
При х = (c + а)
fВ = (qc4 + (4RAa2 - q((c + a)4 - qc4)/a)(c - c - a) + 4RA(c + a - c)3 - q(c + a)4)/24EI = (qc4 + (4RAa2 - q((c + a)4 - qc4)/a)(- a) + 4RAa3 - q(c + a)4)/24EI = (qc4 - 4RAa3 + q((c + a)4 - qc4 + 4RAa3 - q(c + a)4)/24EI = 0
Примечание: по указанным формулам можно получить значение прогиба в любой точке пролета, подставляя соответствующее значение х. | 
