А между тем мы все живем в мире, который значительно сложнее, чем геометрия. Например, стены, потолки и полы квартир и домов, в которых мы живем, в идеале должны представлять собой плоскости, однако далеко не всегда таковыми являются, я уж не говорю про вертикальность и горизонтальность поверхностей. А если это частный дом, то для характеристики поверхности какой-нибудь обмазанной глиной и побеленной стены не хватит и десятка сложнейших тригонометрических уравнений. И никакие обои на такую стену нормально не наклеятся. А уж когда речь заходит об укладке кафельной плитки, то готовить подобные стены к укладке приходится в 3-4 раза дольше, чем укладывать саму плитку.
Правда, сейчас появляется все больше людей, уставших от однообразной правильности плоских поверхностей бетонных коробок. Хочется чего-нибудь нового, каких-нибудь неожиданных изгибов и поворотов. Все это достаточно легко можно реализовать с помощью гипсокартона. Но иногда хочется вытворить нечто подобное и с керамической плиткой.
Вот только плитка в отличие от гипсокартона не гнется (деформациями плитки, возникающими при воздействии соответствующей нагрузки, ввиду их малости можно пренебречь), поэтому поверхность на которую будет наклеиваться плитка, в идеале должна представлять собой не боковую сторону цилиндра, а несколько плоскостей, расположенных друг к другу под определенным углом, проще говоря, сегментов. Впрочем, если плитка достаточно мелкая, а радиус цилиндра достаточно большой, то такую поверхность можно сразу обклеивать плиткой.
Но рассмотрим наиболее неблагоприятный случай, когда ширина плитки достаточно большая, а радиус цилиндра достаточно маленький. Например, при облицовке ванной комнаты плиткой дело дошло до душевого поддона:

Вообще-то в подобных случаях проще воспользоваться наружным уголком или в крайнем случае состыковать две плитки под углом 90°. Однако наружных уголков под рукой не было, а делать прямой угол на проходе, как-то не комильфо - обязательно кто-нибудь об этот угол ударится, да вода может затекать между плитками. К тому же после выполнения основных работ остались обрезки плитки шириной около 1.5 см и я решил их также пустить в дело. Но сначала с помощью стамески и молотка добавил к двум взаимно перпендикулярным плоскостям еще две:

На этой стадии сильно стараться не обязательно. Для того и плитка, чтобы выровнять поверхности. А вот пластиковые внутренние уголки, которые использовались при укладке плитки, следовало прирезать с наибольшей точностью. И тут мне в очередной раз пригодилась геометрия. Потому как, если угол стандартно прямой, то уголки прирезаются под углом 45°, а если фигура - правильный шестигранник, то угол прирезки 60°. У равностороннего треугольника сумма всех углов составляет 180 градусов, соответственно все углы равны 60°, а угол прирезки тогда будет равен 30°. Ну а если количество сторон фигуры стремится к бесконечности то угол прирезки стремится к 90°. Почему так, я никогда сильно не задумывался, просто пользовался полученными в школе знаниями. Но тут при определении угла прирезки мне судя по всему пришлось иметь дело с 12-ти угольником и я включил логическое мышление.
Получается, что любую плоскую геометрическую фигуру с равной длиной сторон можно представить как некоторое количество равнобедренных треугольников с вершинами в центре фигуры, при этом количество треугольников равно количеству сторон фигуры. Тогда квадрат можно образовать 4 равнобедренными треугольниками. Соответственно угол между бедрами такого треугольника будет равен 360/4 = 90°, а остальные два угла треугольников равны между собой и составляют (180 - 90)/2 = 45°. В свою очередь треугольник может быть образован тремя треугольниками, у которых угол между бедрами будет равен 360/3 = 120°, и тогда оставшиеся углы (180 - 120)/2 = 30°. Если продолжить этот логический ряд, то шестиугольник может быть образован шестью треугольниками у которых угол между бедрами составит 360/6 = 60°. А оставшиеся углы (180 - 60)/2 = 60°. Эти вот углы и являются углами прирезки.
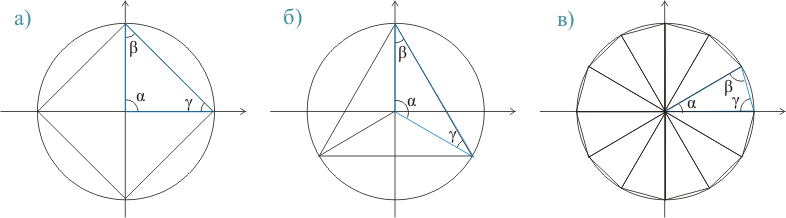
Соответственно для правильного 12-ти угольника угол между бедрами 12 треугольников составит 360/12 = 30°, а 2 других угла составят (180 - 30)/2 = 75°. Ну а если облечь эти рассуждения в математические формулы, то получится:
α - угол вершины равнобедренного треугольника
β = γ - углы между основанием и бедрами равнобедренного треугольника, они же углы прирезки уголков
n - количество сторон геометрической фигуры
тогда
α = 360/n
β = γ = (180 - α)/2
Но так как хорошего стусла у меня под рукой не было и не было даже транспортира, чтобы отложить соответствующие углы, я отпиливал уголки, выставляя угол на глаз. Все равно даже при использовании хорошего стусла возможны погрешности, а внутренний уголок небольшой и проще обработать торцы наждачкой (утюжок у меня всегда под рукой), чем пытаться выдержать положенные градусы (тонкостям подгонки внутренних и наружных уголков со временем будет посвящена отдельная статья).
Примечание: Тут может возникнуть вопрос, почему был выбран угол прирезки, как для правильного 12-ти угольника, ведь длины сторон явно не равны. И тут мы еще на минуту абстрагируемся и представим, что у нас все-таки правильный 12-ти угольник, вот только 2 перпендикулярные стороны его стали бесконечно большими.
Ну а дальше все было относительно просто, так как между плитками всегда делается шов, то и стачивать торцы плитки под углом 75° совсем не обязательно. Достаточно сточить торцы хотя бы немного. После этого на плитку наносится клей:

В данном случае плитка клеилась на деревянный каркас поддона, а потому для пущей надежности использовались жидкие гвозди. Клей наносился пятнами, но справедливости ради следует отметить, что затем, в процессе выставления клей был нанесен сплошным слоем. После приклеивания сегментов плитки поддон выглядел так:

а после наклеивания целых плиток в одной из плоскостей так:

Ну и чтобы снять все сомнения в правильности выбранного метода стыковки были наклеены еще две плитки на перпендикулярную поверхность. Сначала плитки заводились в уголок, а затем на них наносился клей:

После всех этих манипуляций поддон выглядел так:

Вот собственно и все. Осталось только затереть швы затиркой, но это уже совсем другая история. | 
