М = (ql/2)l/2 - (ql/2)l/(2·2) = ql2/4 -ql2/8 = ql2/8 (149.2.3b)
Это, так сказать, каноническое уравнение моментов для балки с шарнирным опиранием, где первая часть уравнения - это опорная реакция ql/2, умноженная на плечо действия силы l/2 (расстояние от точки приложения опорной реакции до рассматриваемой точки, находящейся посредине пролета). А вторая часть уравнения - это площадь эпюры нагрузки ql/2, другими словами распределенная нагрузка, приведенная к сосредоточенной, умноженная на плечо, в данном случае на расстояние от середины пролета до центра тяжести эпюры нагрузки.
Но так как нас в данном случае интересует не построение эпюры моментов, а только значение максимального момента в середине пролета, то нам ничего не мешает рассматривать половину шарнирно опертой балки, на которую действует распределенная нагрузка, как некую жестко защемленную балку длиной l/2. Тогда момент на опоре такой балки составит:
М = - (ql/2)l/(2·2) = - ql2/8 (377.1)
Если мы не будем обращать внимание на знак "-", то полученное значение будет таким же, как и в каноническом уравнении. Пока не совсем понятно зачем понадобилось так курочить каноническое уравнение, но минуточку терпения.
Приведение распределенной равномерно изменяющейся нагрузки к эквивалентной равномерно распределенной.
А теперь внимание. Если нагрузка равномерно изменяется от 0 в начале пролета (х = 0) до q в середине пролета (х = l/2) и затем снова до 0 в конце пролета (x = l), то эпюра такой нагрузки представляет собой треугольник с центром тяжести, расположенным на расстоянии 2/3 от начала пролета (рис. 377.1.а)), площади эпюр и положения центров тяжести для таких эпюр приводятся отдельно, по указанной выше ссылке:
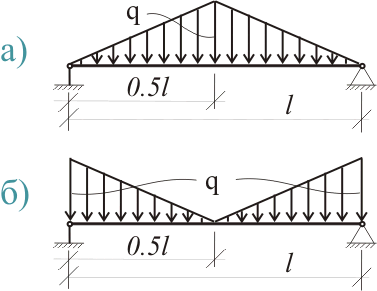
Рисунок 377.1 Эпюры нагрузок, изменение которых описывается линейной зависимостью.
Тогда:
М = ((0 + q)l/2)2l/(3·2) = ql2/12 (377.2)
А если нагрузка равномерно изменяется от q в начале пролета (х = 0) до 0 в середине пролета (х = l/2) и снова до q в конце пролета (х = l), то эпюра такой нагрузки также представляет собой треугольник, но с центром тяжести, расположенным на расстоянии 1/3 от начала пролета (рис. 377.1.б)). Тогда:
М = ((0 + q)l/2)l/(3·2) = ql2/24 (377.3)
Таким образом коэффициент перехода к эквивалентной равномерно распределенной нагрузке в первом случае составляет
k1 = (ql2/12)/(ql2/8) = 2/3 (377.2.1)
а во втором случае
k2 = (ql2/24)/(ql2/8) = 1/3 (377.3.1)
Впрочем получить значение k2 мы можем еще проще. Так как для равномерно распределенной нагрузки k = 1, то k2 = 1 - k1.
Как видим, в данном случае значение коэффициентов совпало с расстоянием от начала координат до центра тяжести эпюры нагрузки.
Приведение распределенной нагрузки, изменение которой описывается квадратичным уравнением, к эквивалентной равномерно распределенной.
Если рассматриваемая распределенная нагрузка описывается квадратным уравнением и изменяется от 0 в начале пролета (х = 0) до q в середине пролета (например мы можем рассматривать эпюру моментов для шарнирно опертой балки при действии равномерно распределенной нагрузки, как ту же эпюру нагрузки), то площадь такой эпюры в середине пролета будет составлять (2/3)ql/2, а расстояние от начала координат до центра тяжести эпюры (5/8)l/2 (рис. 377.2.а)), тогда:
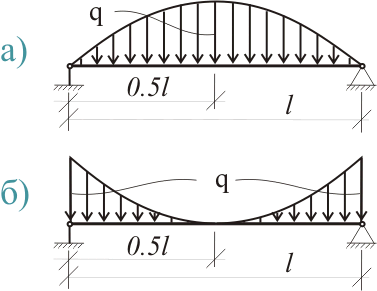
Рисунок 377.2 Эпюры нагрузок, изменение которых описывается квадратичными уравнениями
М = (ql/3)5l/16 = 5ql2/48 (377.4)
Тогда коэффициент приведения
k3 = (5/48)8 = 5/6 (377.4.1)
Если рассматриваемая распределенная нагрузка изменяется от q до 0 в середине пролета и снова до q в конце пролета так, как это показано на рисунке 377.2.б), то мы можем определить коэффициент следующим образом:
k4 = 1 - k3 = 1 - 5/6 = 1/6 (377.5.1)
Подобным образом можно определить значения коэффициентов и для нагрузок, изменение которых описывается другими уравнениями.
И последний вопрос: зачем это нужно, если значения максимальных моментов для указанных видов нагрузок уже определены? Дело в том, что нагрузка не всегда изменяется в указанных пределах. Возможности сочетания распределенных нагрузок поистине беспредельны. Например для некоторой балки значение нагрузки может изменяться линейно от 0.3q в начале координат (х = 0), до q посредине балки (х = l/2) и снова до 0.3q в конце балки (х = l). Таким образом мы имеем как бы сочетание равномерно распределенной нагрузки 0.3q и нагрузки, линейно изменяющейся от 0 до 0.7q в середине пролета и снова до 0 в конце пролета. Тогда эквивалентная равномерно распределенная нагрузка составит 0.3q + 0.7q·2/3 = 0.767q.
Примечание: данный метод определения коэффициентов подходит только при воздействии симметричной нагрузки. Для определения прогибов и углов поворота этот метод также не применим. | 
