Например, когда стропильная нога может рассматриваться как наклонный стержень фермы, имеющей форму прямоугольного треугольника, все более-менее просто и наглядно. Однако подобрать соответствующую расчетную схему для проектируемой кровли бывает достаточно сложно.
Рассмотрим следующую ситуацию. Проектируется кровля, а иногда она бывает уже сделана, и у человека возникает желание как-то усилить конструкцию, например так:

Рисунок 450.1. Геометрическая схема стропильной системы.
На рисунке черным цветом показаны существующие конструкции, а красным (скорее оранжевым) - планируемые. В данном случае нижняя балка называется схваткой, а про верхнюю мы поговорим чуть позже. Так вот, я уже много раз говорил, но не устану повторять, что принятая расчетная схема и реальная работа конструкции - две большие разницы. Мастерство проектировщика в том и состоит, чтобы принять такую расчетную схему, которая наиболее точно соответствует реальной работе конструкции. Между тем выбрать такую расчетную схему не всегда просто и тут вступает в силу одно из основных правил проектировщика - не знаешь, какую расчетную схему принять, принимай самую простую и надежную. Так при расчете на вертикальную нагрузку схватка с в зависимости от выбора расчетной схемы может учитываться, а может и не учитываться. Попробую объяснить, почему.
Первое приближение
Итак стропильную ногу, показанную на чертеже можно рассматривать как наклонную балку, на которую действует вертикальная нагрузка. Если для упрощения расчетов принять угол наклона стропильной ноги 45°, равное расстояние между опорами и не учитывать уже существующей схватки, показанной на чертеже, то расчетная схема для такой стропильной ноги с учетом новой схватки будет выглядеть так:

Рисунок 450.2. Возможная расчетная схема для стропильной ноги с дополнительной горизонтальной опорой
Из уравнений равновесия системы следует, что сумма сил, действующих относительно оси у Σу = 0, а так как у нас никаких горизонтальных сил нет (при расчете на вертикальную нагрузку), то и горизонтальная реакция на опоре В, как впрочем и на опорах А и С равна нулю и на рисунке даже не показана. Именно эту расчетную схему я и рекомендую использовать при расчетах, как более простую и надежную. Впрочем, такие же рекомендации содержатся и в различных руководствах по устройству кровли.
При расчете такой балки рассматривается проекция наклонной балки на ось х, т.е. расчетная длина балки уменьшается и составляет lрасч = lcosa. При этом наклонное сечение, соответствующее главным площадкам напряжений в данной балке в результате проекции становится поперечным сечением балки.
Является ли эта расчетная схема наиболее точно отражающей работу конструкции? Да, если предположить, что и прогиб стропильной ноги происходит вдоль действия вертикальной нагрузки, т.е. по оси у. В этом случае даже при прогибе в 4 см удлинение захватки длиной lcx = 2.8 м составит около Δlcx = 0.3 мм, а таким изменением с учетом местных смятий в опорных узлах можно пренебречь.
Примечание: по теореме Пифагора в прямоугольном прямоугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. l'2 = 2.82 + 0.042 = 7.8416, тогда l' = 2.800285, а Δlсх = 0.000285 м.
Второе приближение
Любую нагрузку, приложенную под углом к нейтральной оси балки, можно разложить на составляющие: вертикальную, действующую перпендикулярно нейтральной оси балки и горизонтальную, действующую параллельно нейтральной оси. А это в свою очередь означает, что при рассмотрении действия составляющих нагрузки какие-то напряжения в горизонтальной опоре возникать все-таки будут. Если рассматривать стропильную ногу под другим углом, проще говоря повернуть наклонную балку так, чтобы она стала горизонтальной, то мы получим балку с как минимум двумя опорами, расположенными под углом к балке. Расчетные схемы для такой балки будут выглядеть так:

Рисунок 450.3. Еще одна возможная расчетная схема для стропильной ноги с горизонтальной подпоркой.
Из этих расчетных схем следует, что как при действии вертикальной, так и при действии горизонтальной нагрузки в опорах В и С, расположенных под углом к балке, будет возникать опорная реакция, которую в свою очередь можно разложить на вертикальную и горизонтальную составляющие.
Примечание: на опоре А у нас мауэрлат, а потому изображать опорные реакции на этой опоре мы можем как угодно.
А так как мы для удобства расчетов приняли угол наклона стропильной ноги 45°, соответственно и опоры В и С находятся к балке под тем же углом, то получается, что как при действии вертикальной, так и горизонтальной нагрузки Вв = -Вг (согласно принятому направлению векторов сил) и Св = Сг. А кроме того в результате действия опорных реакций при вертикальной нагрузке в балке между опорами В и С возникают дополнительные растягивающие напряжения, а при горизонтальной нагрузке на том же участке дополнительные сжимающие напряжения. И если определить горизонтальные составляющие реакций при действии вертикальной нагрузки не составит большого труда - для двухпролетной балки с равными пролетами и равномерно распределенной нагрузкой имеются готовые формулы и эпюры:
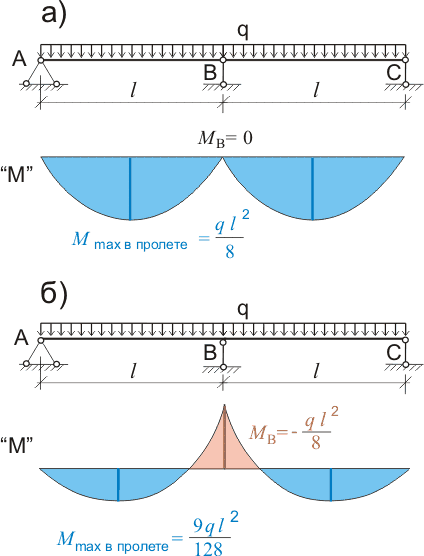
Рисунок 221.1. а) две однопролетные балки с общей опорой; б) двухпролетная балка.
Ав = Св = 3qвl/8 (221.1.7.1),
Bв = 10qвl/8 (221.1.7.3)
Соответственно Вг = -10qвl/8, Cг = 3qвl/8, тогда Аг = 7qвl/8, исходя из того, что сумма всех горизонтальных сил Σх = 0.
Примечание: в данном случае знаки "-" или "+" не означают сжатие или растяжение в рассматриваемых стержнях, а показывают лишь направление векторов сил относительно оси х.
То при действии горизонтальной нагрузки возможны 2 варианта, удовлетворяющие условиям равновесия трижды статически неопределимой системы:
1 вариант: Вг = Сг = 0, Аг = 2qгl. В этом случае вертикальные опорные реакции на всех опорах равны нулю, соответственно никаких дополнительных моментов на рассматриваемую балку действовать не будет и прогиб на опорах также будет равен нулю.
2 вариант: так как согласно первой расчетной схеме сумма сил, действующих на опоре В равна нулю, то при действии горизонтальной составляющей нагрузки -Вв = Вг = 10qгl/8. А значит возникают вертикальные составляющие реакций на опорах А и С, при этом изгибающий момент на крайних опорах всегда равен нулю при центральном приложении нагрузки, а значит Ав = Св = - Вв/2. Тогда, исходя из условий Вг = -Вв и Сг = Св и Σх = Аг + Вг + Сг - 2qгl = 0, мы получим следующее решение: Вг = -Вв = 10qгl/8, Ав = Сг = Св = 5qгl/8, Аг = qгl/8.
1 вариант более приятный, однако менее вероятный. Получается, что у нас изначально горизонтальная опора превратилась чуть ли не в вертикальную. Но так как мы допускаем наличие сжимающих напряжений при вертикальной нагрузке в опоре В, то точно также должны допускать наличие растягивающих напряжений в опоре В при действии горизонтальной нагрузки. И тогда 2 вариант более правильный. Тогда с учетом того, что qв = qг, мы можем вычислить суммарные опорные реакции для нашей балки при действии как вертикальной так и горизонтальной составляющей нагрузки:
Аг = 7qвl/8 + qвl/8 = qвl; Ав = 3qвl/8 + 5qвl/8 = qвl;
-Вг = Вв = 10qвl/8 - 10qвl/8 = 0;
Cг = Cв = 3qвl/8 + 5q2вl/8 = qвl;
А это в свою очередь означает, что мы опять вернулись к 1 расчетной схеме, т.е. к однопролетной балке.
Зачем же тогда нужна схватка? Ну, во-первых, она обеспечивает геометрическую неизменяемость системы, во-вторых кроме вертикальных нагрузок на кровлю действуют и горизонтальные. А в-третьих, центральные стойки устанавливаются под каждой стропильной парой двускатной кровли далеко не всегда и если коньковый прогон имеет достаточно большой прогиб, то он перестает быть опорой С для стропил и в этом случае стропильную систему более правильно рассматривать как треугольную арку с затяжкой, а роль затяжки как раз и выполняет схватка.
И в-четвертых. Если предположить, что деформации в наклонной балке можно рассматривать как и составляющие нагрузки - отдельно. То в такой балке - стропильной ноге будет возникать прогиб от действия вертикальной составляющей нагрузки и растяжение (сжатие) при действии горизонтальной составляющей нагрузки. Рассмотреть, что же при этом происходит, нам поможет
Третье приближение
Решение подобных задач по расчету статически неопределимых конструкций может быть проведено в 4 этапа:
1 этап: Статический аспект задачи
Именно этим аспектом мы до сих пор и занимались, т.е. пытались определить неизвестные силы, исходя из условия статической неизменяемости системы. Однако теперь пришло время поговорить и о других аспектах решения подобной задачи.
2 этап: Геометрический аспект задачи
Так как мы рассматриваем стержни (и стропильную ногу и вертикальную стойку и схватку - горизонтальную опору), гибкость которых далека от бесконечной, то в результате приложения различных сил эти стержни будут деформироваться. А это означает, что изменится геометрия стержня или (и) длина стержня. Так, если рассматривать стропильную ногу как балку на двух опорах (первая расчетная схема), то следует рассматривать 2 вида деформаций - изменение длины Δl при растяжении или сжатии, возникающих в результате действия нормальных сил (горизонтальной составляющей нагрузки), и прогиб f в результате действия вертикальной составляющей нагрузки. Соответственно рассматриваемая точка на нейтральной оси балки будет пытаться изменить свое геометрическое положение. Но такому смещению может препятствовать горизонтальная опора, в которой также может возникнуть изменение длины, показанное на рисунке оранжевым цветом:

Рисунок 450.4. Возможное изменение геометрии рассматриваемой системы.
3 этап: Физический аспект задачи
Изменение длины и прогиб стержней зависят не только от прикладываемых нагрузок, геометрических параметров (длины и размеров поперечного сечения), но и от конкретных физических характеристик стержней, в данном случае от модуля упругости.
Таким образом даже если жесткость горизонтальной затяжки - подпорки равна жесткости основной балки - стропильной ноги, то все равно в силу геометрии рассматриваемой системы горизонтальный стержень не сможет полностью убрать прогиб, а будет с одной стороны уменьшать значение прогиба, а с другой стороны увеличивать изменение длины Δl балки - стропильной ноги. При этом увеличится значение нормальных напряжений в стропильной ноге.
4 этап: Синтез
На основании вышеизложенных положений и производится окончательный расчет. Однако при этом не следует забывать и об еще одном очень важном факторе. Круги на расчетной схеме в точках крепления балки к опорам, подразумевающие возможность свободного вращения балки в этих точках относительно опоры, имеют вполне конкретную материализацию. Например, если горизонтальная схватка будет просто крепиться гвоздями или болтами в нахлест как к стропильной ноге, так и к лежню или стойке (как правило именно так схватки и крепят), то значение Δl для опоры уменьшится из-за местного смятия древесины. А кроме того гвозди должны выдерживать расчетную нагрузку.
Но все равно изменение длины стержня пренебрежимо мало по сравнению с прогибом при действии одной и той же нагрузки и тогда получается, что горизонтальная опора все-таки будет препятствовать прогибу, а значит может рассматриваться как промежуточная вертикальная опора и стропило можно рассматривать как двухпролетную балку и 1 вариант второй расчетной схемы более правильный, только нужно будет учесть уменьшение момента на средней опоре из-за осадки опоры. А эта осадка в свою очередь может рассматриваться, как прогиб консольной балки, если схватка, показанная на рисунке 450.1 сплошная.
А если узел сопряжения стропильной ноги с мауэрлатом позволяет стропильной ноге скользить, то тогда расчет следует производить только по первой расчетной схеме.
Вот такая она - строительная механика. Готовы ли вы рисковать и рассчитывать стропила со схваткой как двухпролетную балку или все-таки лучше рассчитывать ее как однопролетную без учета схватки - решать вам.
А теперь поговорим о самой маленькой верхней схватке, показанной красным цветом на рисунке 450.1. После всего вышесказанного наличие такой схватки кажется и вовсе бессмысленным, однако тут дело обстоит с точностью до наоборот. Если стропильные пары между собой и схватка со стропилами скреплены должным образом. То такая схватка препятствует свободному повороту стропил относительно опоры С, а значит наша балка превращается из однопролетной на двух шарнирных опорах в однопролетную балку с одной шарнирной и второй жестко защемленной опорой.
А это в свою очередь означает, что максимальный момент в пролете значительно уменьшится, при этом на жесткой опоре расчетный момент составит все те же ql2/8, однако воспринимать этот момент будет уже не просто поперечное сечение балки, а узел сопряжения на опоре. Как разложить момент на отдельные силы, можно узнать из других статей, например здесь. В итоге усиление может и понадобится, но усиливать при этом нужно будет не всю балку, а только верхнюю часть. | 
