В принципе я могу предложить один метод, предусматривающий усиление без изменения сечения стропил, а вот понравится он вам или нет - это уже не мне решать.
Итак рассмотрим следующую ситуацию: висячие стропила, представляющие собой треугольную арку с затяжкой или простейшую треугольную ферму (это кому как больше нравится), были выполнены из бруса сечением 15х5 см с шагом 1 м. При этом расстояние между мауэрлатами - пролет арки l = 6 м. Угол уклона кровли - 30°. Впрочем, не будем дальше пересказывать ситуацию, достаточно подробно рассмотренную в различных статьях, например здесь, а просто скажем, что по расчету требуется сечение стропил 15х10 или 20х5 см, т.е. имеющийся момент сопротивления Wz = 187.5 см3 чуть ли не в 2 раза меньше требуемого.
На первый взгляд самым логичным выходом из ситуации будет усиление существующих стропил точно таким же брусом 15х5 см или устройство дополнительных пар стропил, чтобы уменьшить шаг стропил. Но и в первом и во втором случае расходы на усиление будут близки к начальным расходам на устройство стропильной системы.
А между тем есть и другой способ уменьшить значение требуемого момента сопротивления, никогда правда мне не встречавшийся в литературе, посвященной расчету стропильных систем, тем не менее вполне законный с точки зрения теоретической механики.
Всего-то и нужно: изменить расчетную схему.
Как мы знаем, в поперечном сечении посредине однопролетной балки с шарнирными опорами при действии равномерно распределенной нагрузки возникает изгибающий момент, равный М = ql2/8. А у такой же балки, но с жестким защемлением на опорах максимальный момент возникает на опорах и составляет M = ql2/12, т.е. в 1.5 раза меньше.
Таким образом, если для стропильной системы, показанной на рисунке 462.1.а) (принимаемая расчетная схема показана на рисунке 462.1.б)), мы поставим схватки между стропилами в коньке и между стропилами и затяжкой примерно так, как это показано на рисунке 462.1.в), то полученную систему мы можем рассматривать, как арку из одного стержня с жестким защемлением на опорах (хотя это будет и не совсем правильно).
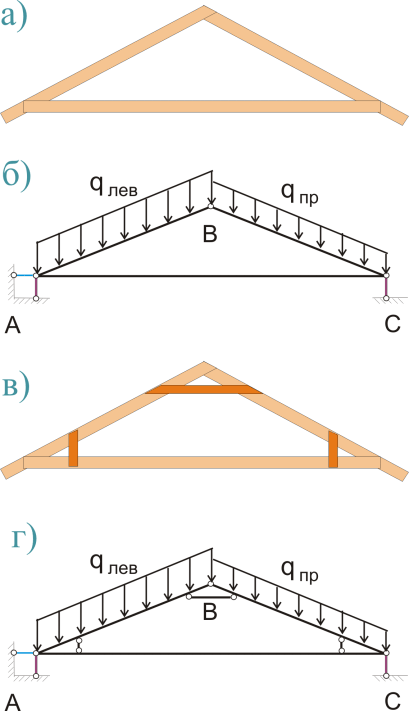
Рисунок 462.1. Трехшарнирная арка и одностержневая арка с жестким защемлением на опорах
Такая арка является статически неопределимой, но мы можем упростить задачу, если будем рассматривать стропила как жестко защемленные наклонные балки или как двухпролетные балки на 2 шарнирных и одной жестко защемленной опорах. Только не будем при этом забывать, что на стержни арки действуют нормальные силы, определенные нами ранее.
Сначала рассмотрим наиболее простой вариант:
стропила - наклонная однопролетная балка с жестким защемлением
Как видно из расчетной схемы, приведенной на рисунке 462.1.г), дополнительные стержни не только создают условия, при которых стропила можно рассматривать как защемленную балку, но еще и уменьшают расчетную длину пролета. Так наклонная проекция стропил - трехшарнирной арки с затяжкой, составляла 3 м. Если же мы разместим вертикальные захватки так, что в горизонтальной проекции это составит по 0.5 м с каждой стороны, то только уменьшение расчетного пролета на а = 0.5 м или на (1/6) приведет к уменьшению момента в 1.44 раза, так как
(l - l/6)2/l2 = (25l2/36)/l2 = 25/36 ≈ 0.7.
Примечание: горизонтальную схватку между стропилами нельзя рассматривать как дополнительную вертикальную опору.
Таким образом общее уменьшение максимального момента составит 1.5·1.44 = 2.16 раз, чего в данном случае вполне достаточно. В численном выражении максимальные изгибающие моменты на опорах защемленной наклонной балки составят:
Mcmax = ql2/12 = 326.1·2.52/12 = 169.844 кгс·м или 16984.4 кгс·см
Такой же момент будет создавать сила, приложенная вертикально на расстоянии 0.5 м от основной опоры и составляющая:
Р = 169.844/05 = 339.7 кг
А значит для крепления вертикальной схватки достаточно:
n = P/T = 339.7/87.5 = 3.88 точнее 4 гвоздя диаметром 0.5 см.
Такое же количество гвоздей можно принять и для крепления горизонтальной схватки, если узел крепления находится на расстоянии о.5 м от стрелы арки в горизонтальной проекции.
Теперь осталось проверить, выдержит ли затяжка дополнительную нагрузку - две сосредоточенные силы Р, приложенные на расстоянии 0.5 м от каждой опоры. Согласно расчетной схемы 1.3 из таблицы 1. максимальный момент в поперечных сечениях затяжки составит:
Mз = Ра = 339.7·0.5 = 169.844 кгс·м = Мcmax
Тогда требуемый момент сопротивления для затяжки:
Wzтр = M/R = 16984.4/140 = 121.32 см3
Между тем у нас затяжка имеет сечение 10х5 см и соответственно момент сопротивления W = bh2/6 = 5·102/6 = 83.33 см3, т.е. в 1.45 раза меньше требуемого и это еще без учета растягивающих напряжений, действующих в поперечных сечениях затяжки.
Если уменьшать расстояние от опоры до вертикальной схватки, то это будет только увеличивать значение изгибающего момента в стяжке, да и количество гвоздей придется увеличивать. А если увеличивать расстояние от опоры до вертикальной схватки, то такую конструкцию уже вряд ли можно рассматривать как жестко закрепленную балку.
И тут вроде бы другого выхода нет, как усиливать затяжку, но если сделать схватки не вертикальные, а под некоторым углом к вертикали, например 35-40°, то такая схватка превратится с одной стороны в вертикальную опору, а с другой в горизонтальную, увеличивающую растяжение в затяжке, оставаясь при этом элементом, обеспечивающим жесткое защемление стропил.
Проверяем. Расчетная длина вертикальной схватки равна:
lвcx = tg30°a = 0.5773·0.5 = 0.2887 м
При угле наклона 35° расстояние а' от наклонной схватки до места, где была бы вертикальная схватка составит:
a' = tg35°lвсх = 0.7·0.2887 = 0.2 м
Тогда изгибающий момент, действующий на затяжку, составит:
Мз = Р(a - a') = 339.7(0.5 - 0.2) = 101.18 кгс·м
Увеличение нормальной силы, действующей на затяжку составит:
N' = Psina/cosa = 339.7·0.573/0.819 = 237.86 кг
Тогда максимальные нормальные напряжения, возникающие в поперечных сечениях затяжки, с учетом разности расчетных сопротивлений растяжению и изгибу древесины составят:
(N + N')/F + MзRp/WzRи = (692.927+ 237.86)/50 + 10180·101.9/(83.33·142.7)= 18.61 + 87.26 = 105.9 кг/см2 > Rр = 101.9 кг/см2
Необходимые условия по прочности нами не соблюдены. Впрочем превышение напряжений составляет менее 4%. С учетом принятых коэффициентов надежности по нагрузке такое превышение можно считать допустимым, а можно еще немного увеличить угол наклона. Это уже на ваш выбор.
Кроме того в действительности значение изгибающего момента будет немного больше, особенно если на участок стропила между наклонной схваткой и мауэрлатом будут опираться доски обрешетки.
При наклонных захватках количество гвоздей также следует увеличить:
n = P/(Tcos35°) = 3.88/0.819 = 4.7 точнее 5 гвоздей.
Если рассматривать стропила, как двухпролетную балку с двумя шарнирными и одной жестко защемленной опорой, то момент на опоре - вертикальной (или наклонной) схватке будет немного меньше, а на жесткой опоре - стреле арки - немного больше. Впрочем и такая расчетная схема не является точно отображающей реальную работу конструкции.
Тем не менее подобный расчет можно произвести, например с использованием метода трех моментов. Ну а для всех остальных совет: добавьте по 1-2 гвоздя в узлах крепления стропил и стяжки со схватками. | 
