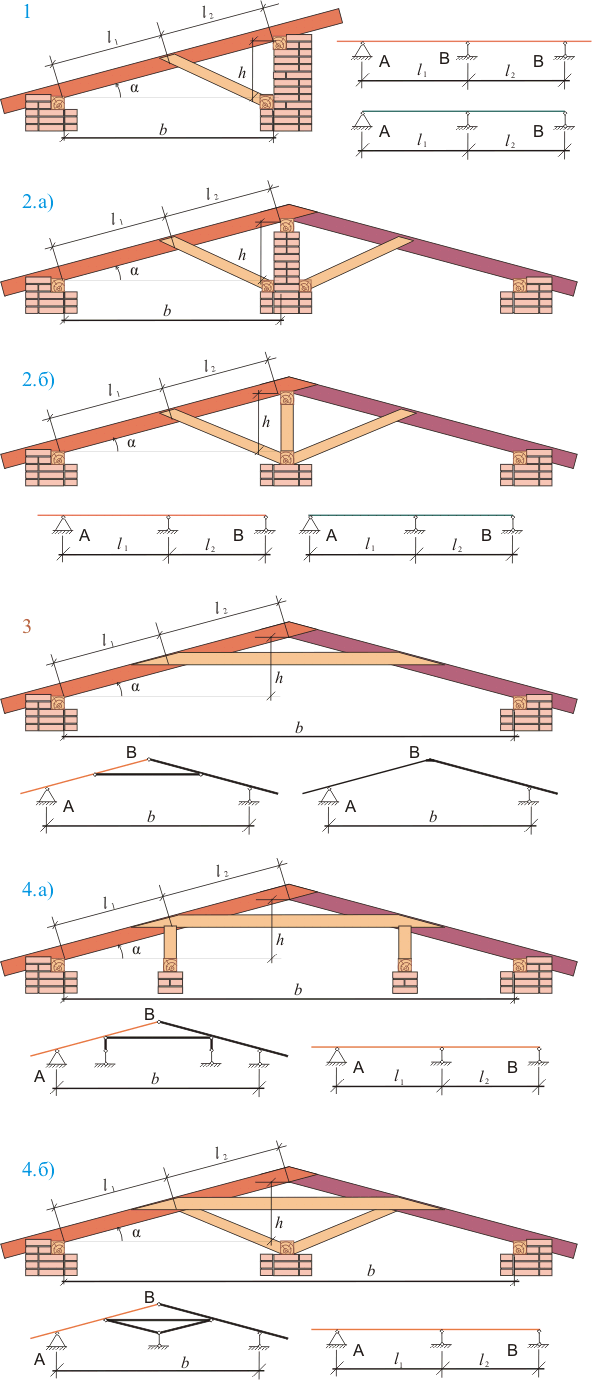
Рисунок 227.2. Возможные расчетные схемы стропил - двухпролетных неразрезных балок.
Стропильные системы, показанные на рисунках 227.2.1 и 227.2.2 можно рассматривать как двухпролетные неразрезные балки (впрочем стропила этих стропильных систем можно рассматривать и как верхние пояса ферм, на результатах расчета это никак не отразится). Такие стропила относятся к наслонным.
Стропильная система, показанная на рисунке 227.2.3 может рассматриваться как треугольная арка с затяжкой выше опор. Такие стропила относятся к висячим.
А вот стропильные системы, показанные на рисунке 227.2.4 вроде как и наслонные, представляющие собой все те же двухпролетные неразрезные балки, а вроде как и висячие, потому как есть затяжка. Как быть в таком случае?
Ответ простой: подобные стропила следует рассчитывать как двухпролетные неразрезные балки, т.е. как наслонные стропила, но при этом учитывать возникновение дополнительных нормальных напряжений из-за наличия затяжки.
Для начала рассмотрим стропильную систему, показанную на рисунке 227.2.4.а)
Подробности расчета двухпролетных неразрезных балок на действие распределенной нагрузки изложены отдельно, здесь же скажу, что если рассматривать горизонтальную проекцию стержня на ось х и длина пролетов l1cosa = l2cosa = b/4, и не учитывать наличие консолей, то расчеты значительно упрощаются. При симметричной нагрузке вертикальные опорные реакции на опорах А и В будут равны и составят:
А = В = 3qb/(8·4) = 3qb/32 (470.1.1)
Вертикальная опорная реакция на промежуточной опоре, назовем ее D, составит
D = 10qb/(8·4) = 10qb/32 (470.1.2)
Максимальный изгибающий момент будет действовать в поперечном сечении стропила на промежуточной опоре D и составит:
M = qb2/(8·4) = qb2/32 (470.1.3)
Теперь нужно определить нормальные силы, действующие в затяжке и верхней части стропил - наклонных стержней.
Если бы у нас была трехшарнирная арка с двумя вертикальными опорами на концах арки и затяжкой выше вертикальных опор, т.е. на высоте, равной половине стрелы арки f/2, то определение нормальных сил большого труда не составило бы. Тогда нормальная сила, действующая на затяжку, согласно уравнению моментов для правой части арки относительно точки В:
Nз = 2(- qb2/8 + qb2/4)/f = qb2/4f (470.2.1)
А если рассматривать трехшарнирную арку с длиной пролета b/2 и стрелой арки f/2 с затяжкой на опорах, то
Nз = 2(- qb2/32 + qb2/16)/f = qb2/16f (470.2.2)
Соответственно нормальная сила в верхней части стропильной ноги
Nс = Nзcosa (470.3.1)
Вот только у нас арка не с 2, а с 4 вертикальными опорами. Такая арка является дважды статически неопределимой. Тем не менее с точки зрения теоретической механики ничто не мешает нам рассматривать простую трехшарнирную арку с затяжкой на опорах, если мы мысленно удалим нижние части наклонных стержней, а вместо них приложим на этих опорах изгибающие моменты и поперечные силы. Статическое равновесие системы при этом по-прежнему будет соблюдаться. При этом расчетная схема такой арки будет выглядеть так:
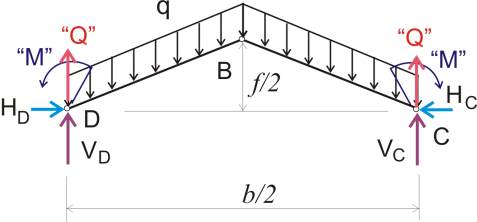
Рисунок 470.1. Расчетная схема для арки с учетом моментов и поперечных сил.
Как видим, данная расчетная схема очень похожа на расчетную схему для арки с жестким защемлением на опорах, отличие только в том, что мы учитываем поперечные силы отсеченных нижних частей наклонных стержней. Так как при симметричной нагрузке изгибающие моменты на опорах D и С равны и направлены в противоположные стороны, то наличие этих моментов никак не повлияет на значение опорных реакций:
VD = VC = qb/4 (470.4.1)
При этом поперечные силы Q будут составлять:
Q = 5qb/32 (470.4.2)
Почему так, достаточно подробно рассматривается в статье, посвященной расчету двухпролетных неразрезных балок, здесь на этом останавливаться не будем, лишь отметим, что опорная реакция на промежуточной опоре двухпролетной балки - это и есть сумма поперечных сил справа и слева от опоры.
Соответственно опорные реакции НD = HC или нормальная растягивающая сила в затяжке согласно уравнению моментов относительно точки В:
Nз = 2(- qb2/32 - М + VDb/4 + Qb/4)/f = 2( -qb2/32 - qb2/32 + qb2/16 +5qb2/128)/f = 5qb2/64f = qb2/12.8f (470.2.3)
Как видим, нормальная сила, действующая на затяжку, при более точном расчете все-таки больше, чем при упрощенном расчете (рассмотрении просто трехшарнирной арки с затяжкой на опорах).
Для определения момента сопротивления поперечного сечения стропил достаточно разделить значение максимального момента на расчетное сопротивление материала, из которого будут изготавливаться стропила:
Wтреб = M/R (470.5)
Если стропила будут изготавливаться из металлических профилей, то при расчетах следует учесть влияние поперечной силы на промежуточной опоре.
Для деревянных конструкций следует дополнительно определить площадь опорной площадки стропил на вертикальные стойки:
F = (VD + Q)/Rсм (470.6)
Впрочем и для металлических конструкций такой расчет может понадобиться.
Примечание: Конечно же расчетные нагрузки далеко не всегда симметричны, к тому же дополнительные вертикальные опоры вряд ли будут на расстоянии b/4 от наружных стен - крайних опор. Это означает, что затяжка будет выше середины стрелы арки и пролеты у балок будут разными. Тут потребуется более долгий расчет, тем не менее выполнить его, руководствуясь вышеизложенными положениями, большого труда не составляет.
А теперь рассмотрим стропильную систему, показанную на рисунке 227.2.4.б)
Формальная разница между расчетными схемами, показанными на рис. 227.2.4.а) и 227.2.4.б) лишь в том, что в затяжке и в верхней части стропил будут возникать дополнительные растягивающие и сжимающие напряжения из-за того промежуточные опоры не вертикальные стержни - стойки, а наклонные стержни - подкосы.
При принятой нами геометрии арки (затяжка находится посредине стропильных ног) нормальная растягивающая сила, действующая на затяжку увеличится в 2 раза.
В общем случае для определения дополнительных растягивающих сил в затяжке нужно умножить суммарное значение вертикальной опорной реакции и поперечной силы, которую теперь воспринимает не вертикальная стойка, а подкос, на синус угла β между вертикальной опорной реакцией и подкосом, а затем разделить на косинус этого угла:
Nздоп = (VD + Q)sinβ/cosβ (470.7.1)
Так при вертикальной стойке β = 0°, соответственно Nздоп = (V + Q)0/1 = 0
Этим же правилом можно пользоваться и тогда, когда есть две внутренние стены, как при расчетной схеме, показанной на рисунке 227.2.4.а), но при этом расстояния между стенами одинаковые, тем не менее затяжка делается посредине длины стропил. Соответственно на внутренние стены опираются не стойки, а подкосы.
Для определения дополнительной продольной силы, действующей на подкосы, нужно разделить суммарное значение вертикальной опорной реакции и поперечной силы на косинус угла β:
Nпдоп = (VD + Q)/cosβ (470.7.2)
Впрочем, если рассматривать эту конструкцию, как арку на 4 вертикальных опорах, то сумма вертикальной опорной реакции и поперечной силы - это и есть опорная реакция на опоре D для арки с 4 вертикальными опорами.
Примечание: расчетные нагрузки далеко не всегда являются симметричными, а это значит, что подкосы могут вызывать распор на внутренней стене. Чтобы этого не случилось, затяжку лучше крепить ниже середины стропил и при этом дополнительно скреплять затяжку с подкосами.
Данных теоретических предпосылок как правило достаточно для расчета стропильных систем, показанных на рисунке 227.2.4 или близких к ним. Впрочем бывают и другие варианты стропильных систем. | 
