Определение прогиба фанерного листа
Итак имеется ячейка с размерами в свету 50х50 см, которую планируется зашить фанерой толщиной h = 1 см (вообще-то согласно ГОСТ 3916.1-96 толщина фанеры может быть 0.9 см, но мы для упрощения дальнейших расчетов будем считать, что у нас фанера толщиной 1 см), на фанерный лист будет действовать плоская нагрузка 300 кг/м2 (0.03 кг/см2). На фанеру будет наклеиваться керамическая плитка, а потому очень желательно знать прогиб фанерного листа (расчет фанеры на прочность в данной статье не рассматривается).
Соотношение h/l = 1/50, т.е. такая пластина является тонкой. Так как мы технически не сможем обеспечить такое крепление на опорах, чтобы лаги воспринимали горизонтальную составляющую опорной реакции, возникающую в мембранах, то и рассматривать фанерный лист, как мембрану, не имеет смысла, даже если ее прогиб будет достаточно большой.
Как уже отмечалось, для определения прогиба пластины можно воспользоваться соответствующими расчетными коэффициентами. Так для квадратной плиты с шарнирным опиранием по контуру расчетный коэффициент k1 = 0.0443, а формула для определения прогиба будет иметь следующий вид
f = k1ql4/(Eh3)
Формула вроде бы не сложная и почти все данные для расчета у нас есть, не хватает только значения модуля упругости древесины. Вот только древесина - анизотропный материал и значение модуля упругости для древесины зависит от направления действия нормальных напряжений.
Так, если верить нормативным документам, в частности СП 64.13330.2011, то модуль упругости древесины вдоль волокон Е = 100000 кгс/см2, а поперек волокон Е90 = 4000 кг/см2, т.е. в 25 раз меньше. Однако для фанеры значения модулей упругости принимаются не просто, как для древесины, а с учетом направления волокон наружных слоев согласно следующей таблицы:
Таблица 475.1. Модули упругости, сдвига и коэффициенты Пуассона для фанеры в плоскости листа

Можно предположить, что для дальнейших расчетов достаточно определить некое среднее значение модуля упругости древесины, тем более, что слои фанеры имеют перпендикулярную направленность. Однако такое предположение будет не верным.
Более правильно рассматривать соотношение модулей упругости, как соотношение сторон, например для березовой фанеры b/l = 90000/60000 = 1.5, тогда расчетный коэффициент будет равен k1 = 0.0843, а прогиб составит:
f = k1ql4/(Eh3) = 0.0843·0.03·504/(0.9·105·13) = 0.176 см
Если бы мы не учитывали наличие опирания по контуру, а производили расчет листа, как простой балки шириной b = 50 см, длиной l = 50 см и высотой h = 1 см на действие равномерно распределенной нагрузки,то прогиб такой балки составил бы (согласно расчетной схеме 2.1 таблицы 1):
f = 5ql4/(384EI) = 5·0.03·50·504/(384·0.9·105·4.167) = 0.326 см
где момент инерции I = bh3/12 = 50·13/12 = 4.167 см4, 0.03·50 - приведение плоской нагрузки к линейной, действующей по всей ширине балки.
Таким образом опирание по контуру позволяет уменьшить прогиб почти в 2 раза.
Для пластин, имеющих одну или несколько жестких опор по контуру, влияние дополнительных опор, создающих контур, будет меньше.
Например, если лист фанеры будет укладываться на 2 смежные ячейки, и мы будем рассматривать его как двухпролетную балку с равными пролетами и тремя шарнирными опорами, не учитывая опирание по контуру, то максимальный прогиб такой балки составит (согласно расчетной схемы 2.1 таблицы 2):
f = ql4/(185EI) = 0.03·50·504/(185·0.9·105·4.167) = 0.135 см
Таким образом укладка фанерных листов как минимум на 2 пролета позволяет уменьшить максимальный прогиб почти 2 раза даже без увеличения толщины фанеры и без учета опирания по контуру.
Если учитывать опирание по контуру, то мы имеем как бы пластину с жестким защемлением по одной стороне и шарнирным опиранием по трем остальным. В этом случае соотношение сторон l/b = 0.667 и тогда расчетный коэффициент будет равен k1 = 0.046, а максимальный прогиб составит:
f = k1ql4/(Eh3) = 0.046·0.03·504/(0.9·105·13) = 0.096 см
Как видим, разница уже не столь значительная, как при шарнирном опирании по контуру, но в любом случае почти двукратное уменьшение прогиба при наличии жеского защемления по одной из сторон может оказаться очень полезным.
Ну а теперь мне хотелось бы сказать пару слов о том, почему модули упругости для фанеры различаются в зависимости от направления волокон, ведь фанера такой хитрый материал, в котором направления волокон в соседних слоях перпендикулярны.
Определение модуля упругости фанерного листа. Теоретические предпосылки
Если предположить, что модуль упругости каждого отдельно взятого слоя фанеры зависит только от направления волокон и соответствует модулю упругости древесины, т.е. пропитка, прессовка во время изготовления и наличие клея на значение модуля упругости не влияют, то сначала следует определить моменты инерции для каждого из рассматриваемых сечений.
В фанере толщиной 10 мм как правило имеется 7 слоев шпона. Соответственно каждый слой шпона будет иметь толщину примерно t = 1.43 мм. В целом приведенные сечения относительно перпендикулярных осей будут выглядеть примерно так:
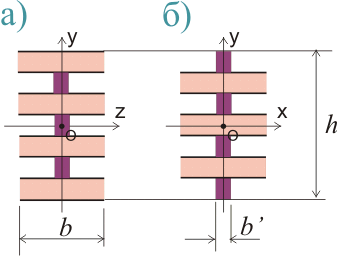
Рисунок 475.1. Приведенные сечения для фанерного листа толщиной 10 мм.
Тогда, принимая ширину b = 1, а b' = 1/24, мы получим следующие результаты:
Iz = t(2(3t)2 + t(2t2) + 4·t3/12 + 2t(2t2)/24 + 3t3/(24·12) = t3(18 + 2 + 1/3 + 1/3 + 1/96) = 1985t3/96 = 20.67t3
Ix = t(2(3t)2/24 + t(2t2)/24 + 4·t3/(12·24) + 2t(2t2) + 3t3/12 = t3(18/24 + 2/24 + 1/72 + 8 + 6/24) = 655t3/72 = 9.1t3
Если бы модули упругости были одинаковыми во всех направлениях, то момент инерции относительно любой из осей составлял бы:
I'x = t(2(3t)2 + t(2t2) + 4·t3/12 + 2t(2t2) + 3t3/12 = t3(18 + 2 + 1/3 + 8 + 1/4 =433/12 = 28.58t3
Таким образом, если не учитывать наличие клея и других вышеперечисленных факторов соотношение модулей упругости составило бы 20.67/9.1 = 2.27, а при рассмотрении фанерного листа, как балки, модуль упругости вдоль волокон наружных слоев составил бы (20.67/28.58)105 = 72300 кгс/см2. Как видим, технологии, используемые при изготовлении фанеры, позволяют увеличить расчетное значение модулей упругости, особенно при прогибе листа поперек волокон.
Между тем, соотношение расчетных сопротивлений при изгибе вдоль и поперек волокон наружных слоев (которые тоже можно рассматривать, как соотношение моментов инерции) гораздо ближе к определенному нами и составляет примерно 2.3-2.4.
Такие дела. | 
