Расчет простых однопролетных рам на действие вертикальной нагрузки

Разнообразие возможных видов рам настолько велико, что не поддается ни какому описанию, да в этом и нет необходимости. Если действующие нагрузки, геометрические параметры и жесткости элементов рамы известны, то достаточно определить, какая это рама: плоская или пространственная и какая у этой рамы степень статической неопределимости.

Затем можно переходить от заданной системы к основной, строить эпюры единичных моментов, поперечных и продольных сил, одним словом заниматься расчетом рамы одним из многочисленных методов, существующих на сегодняшний день. Но в данной статье мне хотелось бы поговорить не об этом, а о том, как можно перейти от расчетов статически неопределимых балок к расчету рам, по умолчанию являющихся статически неопределимыми конструкциями, точнее наоборот.

Пример расчета простой рамы с шарнирными опорами

Если рама, состоящая из 3 элементов имеет простую прямоугольную или квадратную форму, как показано на рисунке 487.1.а), то такую раму достаточно легко рассчитать, если рассматривать ее как неразрезную трехпролетную балку (рис.487.1.б)):

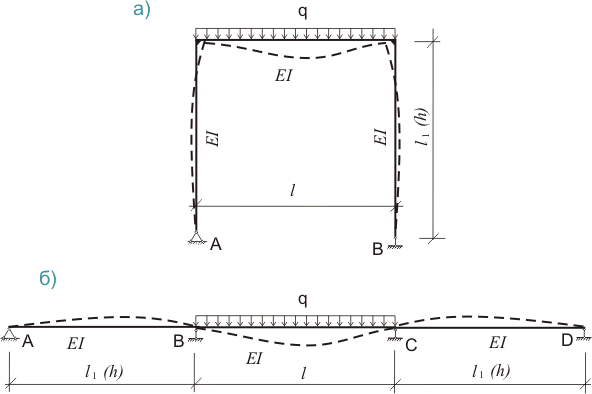
Рисунок 487.1. а) простая рама б) расчетная схема, принимаемая при рассмотрении простой рамы как трехпролетной неразрезной балки

В принципе, в этом нет ничего удивительного, по сути простейшая рама - это и есть ломаная неразрезная балка, степень статической неопределимости такой рамы равна 2, как и для трехпролетной неразрезной балки. Вот только форма рамы значительно отличается от прямолинейной балки.

В связи с этим моменты, действующие в различных сечениях такой рамы, будут такими же как и для неразрезной трехпролетной балки. А в местах перехода из горизонтального элемента рамы в вертикальные элементы касательные напряжения, действующие в крайних поперечных сечениях горизонтального элемента, будут превращаться в нормальные напряжения, действующие в вертикальном элементе, а нормальные напряжения, действующие в горизонтальном элементе - в касательные напряжения в вертикальных элементах. Ну и наоборот касательные напряжения в вертикальных элементах будут превращаться в нормальные напряжения в горизонтальном элементе.

Таким образом, если рассматривать данную раму как балку, то для дальнейших расчетов можно воспользоваться уравнениями трех моментов. При l = l₁ и при постоянной жесткости элементов EI расчеты значительно упрощаются. Тогда

2M_B(2l) + M_Cl = - 6·R^ф₁;

M_Bl + 2M_C(2l) = - 6·R^ф₂; (315.4.1)

где

R^ф₁ = R^ф₂ = В^ф = А^ф = ql³/24

Так как наша балка является симметричной и приложенная нагрузка является симметричной и соответственно М_В = М_С, то мы сразу можем определить значение моментов:

M_B = M_С = - 6(ql³/24)/5l = - ql²/20

Чтобы определить момент в середине среднего пролета, нужно сначала вычислить значения опорных реакций, впрочем, при выбранной схеме загружения трехпролетной балки это будет сделать опять-таки не сложно:

Для первого пролета:

Аl = M_B;  A = ( - ql²/20)/l = - ql/20

Для 2 пролета:

A(2l) + Bl - ql²/2 = M_C;  B = (-ql²/20  + ql²/10 + ql²/2)/l = 11ql/20

тогда максимальное значение момента в среднем пролете (в середине горизонтального элемента рамы) составит

M_max = A(1.5l) + B(0.5l) - ql²/8 = - 3l²/40 +11l²/40 - 5ql²/40 = 3ql²/40

Для проверки расчетов следует убедиться, то прогиб равен нулю на опорах. Для этого нужно сначала определить угол поворота на опоре А:

f_B = tgΘ_Al + Al³/6EI = 0;

тогда

tgΘ_A = - Аl²/6EI = - (- ql³/(20·6EI)) = ql³/120EI;

при таком тангенсе угла наклона на опоре А прогиб на опоре С составит:

f_С = 2ltgΘ_A + A(2l)³/6EI + Bl³/6EI - ql⁴/24EI = 2ql⁴/120EI - 8ql⁴/120EI +  11ql⁴/120EI - 5ql⁴/120EI = 0;

Вроде бы мы нигде не ошиблись и на основании полученных данных можно построить все необходимые эпюры как для балки, так и для рамы.

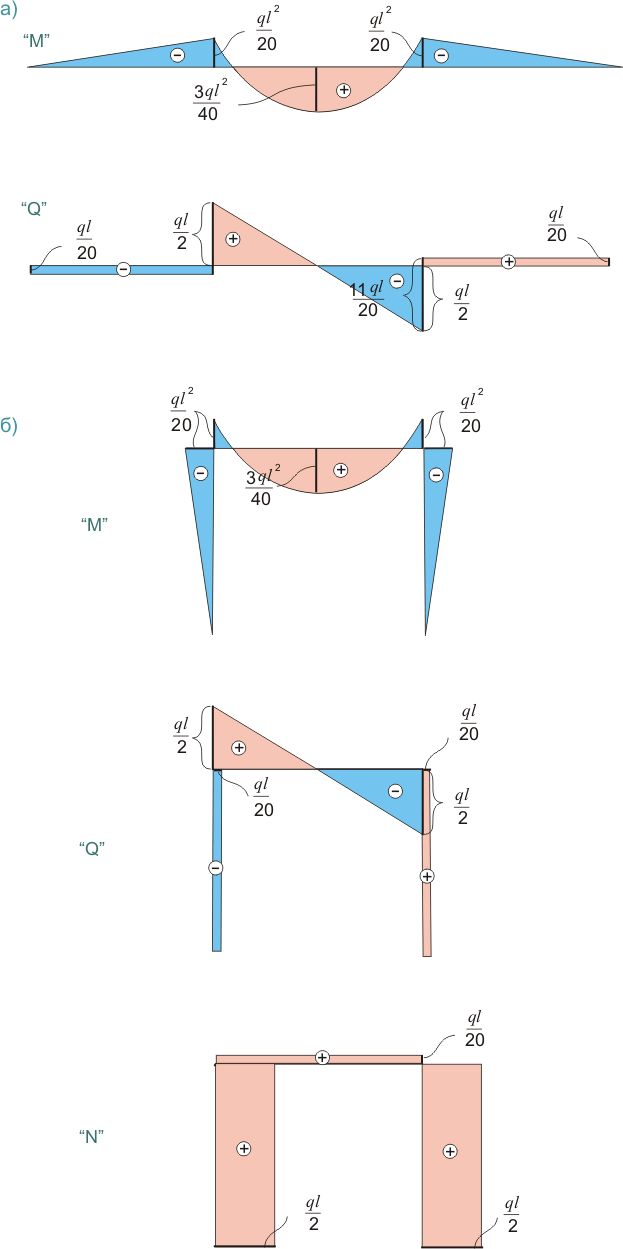
Рисунок 487.2. Эпюры для трехпролетной балки и для рамы.

Примечание: Вообще-то для стоек рамы принято считать, что если действие момента приводит к растяжению правой части сечения вертикальной стойки, то такой момент считается положительным, а если к растяжению левой части сечения, то отрицательным. В связи с этим знак на эпюре "М" для правой стойки должен быть положительным, однако для наглядности я оставил такие знаки, которые соответсвуют эпюрам неразрезной трехпролетной балки.

А вот если размеры рамы будут другие или у вертикальных элементов и горизонтального будет разная жесткость, то конечные эпюры будут иметь другой вид.

Чем меньше будет длина вертикальных элементов, тем больше в итоге будет момент на краях горизонтального элемента и тем меньше посредине. При l1 → 0 М_оп → - ql²/12, М_пр → ql²/24 (для горизонтального элемента), т.е. такая рама, точнее ее горизонтальный элемент, будет все больше напоминать обычную однопролетную балку с жестким защемлением на опорах. Подобная же ситуация будет и в том случае, если жесткость вертикальных элементов будет значительно больше, чем жесткость горизонтального.

Но как правило в простых рамах, используемых в малоэтажном строительстве, жесткость горизонтального элемента значительно больше жесткости вертикальных элементов и в этом случае М_оп → 0, М_пр → ql²/8 (для горизонтального элемента), т.е. такая рама, точнее ее горизонтальный элемент, будет все больше напоминать обычную балку на шарнирных опорах.

Все это позволяет не то, чтобы рассчитать, но предварительно оценить нагрузки на элементы простых рам, не погружаясь в точные расчеты.

А еще примечательно то, что если у рамы будет как бы один горизонтальный элемент и сколь угодно много вертикальных, то при равномерно распределенной нагрузке на горизонтальный элемент принципы расчета, изложенные в данной статье, тоже годятся, если рассматривать все промежуточные вертикальные элементы просто как шарнирные опоры многопролетной балки для упрощения расчетов.

Тем не менее, для более точных расчетов неободимо учитывать появление углов поворота на промежуточных опорах неразрезной балки. Эти углы поворота будут приводить к появлению изгибающего момента в промежуточных вертикальных элементах, впрочем довольно незначительному.

Пример расчета простой рамы с жестким защемлением на опорах

Если у рассматриваемой рамы будет не шарнирное опирание, а жесткое защемление на концах, то такая рама будет 4 раза статически неопределимой для расчета такой рамы потребуется составить 4 уравнения, правда решить их будет сложнее. Жесткие защемления на концах при этом заменяются на шарнирные опоры и добавляются условные дополнительные пролеты нулевой длины. Соответственно возникают моменты на опорах А и D.

Такой расчет займет гораздо больше времени, однако на конечный результат сильно не повлияет при нагрузке, действующей только на горизонтальный элемент.

Тем не менее и тут расчеты можно значительно упростить, так как мы знаем, что в балке с жестким защемлением на одной опоре и с шарнирным опиранием на другой при действии момента на шарнирной опоре в жестком защемлении возникает опорный момент, имеющий в 2 раза меньшее значение и противоположного знака. Тогда

M_Al + 2M_B(2l) + M_Cl = - ql³/4;

M_Bl + 2M_C(2l) +M_Dl = - ql³/4;

При М_А = М_D = - М_В/2, и М_В = М_С, мы получаем следующие уравнения:

- M_Вl/2 + 5M_Bl = - ql³/4;

M_В = - ql²/(4·4.5) = - ql²/18

Соответственно

М_А = - (- ql²/18)/2 = ql²/36

Примечание: тот же результат мы бы получили, составив полную систему из 4 уравнений. Первое уравнение при этом имело бы вид (с учетом нулевой длины дополнительного пролета):

2М_А(l + 0) + M_Bl = 0

преобразовав которое мы получим:

2M_A = - M_B

M_A = - M_B/2

Как видим, наличие жесткости на опорах рамы немного увеличивает значение момента на краях горизонтального элемента и немного уменьшает значение момента в пролете горизонтального элемента (вычисление момента в пролете здесь не приводится, добавлю только, что выполнить его можно по приведенному выше алгоритму).

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

На главную

• Расчет конструкций ::: Основы строймеха и сопромата ::: Рамы

Комментариев нет

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).