Сразу скажу, при симметричной вертикальной нагрузке на раму влияние промежуточных стоек на общий расчет относительно не велико. Поэтому можно сразу задаться соответствующим коэффициентом надежности по нагрузке, например γн = 1.1 и рассчитывать раму, как простую неразрезную балку.
Более того, если пролетов у рамы много и они равные по длине, то промежуточные горизонтальные элементы вообще можно рассчитывать как однопролетную балку с жестким защемлением на опорах, а крайние, как балку с жестким защемлением на одной опоре и шарнирной опорой на другой, если задаться коэффициентом надежности по нагрузке еще большего значения, хотя при этом учитывать наличие момента на шарнирной опоре все-таки желательно.
Тем не менее, продолжим.
Когда мы рассматриваем любую многопролетную неразрезную балку, то полагаем, что промежуточные шарнирные опоры препятствуют только вертикальному перемещению оси балки, но никак не повороту поперечного сечения относительно оси z.
Между тем в многопролетной раме промежуточные вертикальные стойки будут сопротивляться повороту поперечного сечения, если такой поворот будет, и таким образом примут часть нагрузки (а точнее, момента) на себя. Насколько сильно - зависит от множества факторов. Варианты приложения нагрузки, длины пролетов, размеры вертикальных стоек, жесткости вертикальных и горизонтальных элементов как раз и являются такими факторами.
Максимальное влияние на изменение угла поворота окажут промежуточные стойки с нулевой длиной или бесконечно большой жесткостью (и то и другое далеко от реальности, но теоретически возможно), т.е. при наличии таких стоек угол поворота на промежуточных опорах всегда будет равен нулю, горизонтальные элементы можно рассчитывать как балки с соответствующим количеством защемлений на опорах.
Никакого влияния на изменение угла поворота не окажут промежуточные стойки с бесконечно большой длиной или нулевой жесткостью. Наличие таких промежуточных стоек можно вообще не учитывать и рассчитывать горизонтальные элементы просто как многопролетную неразрезную балку.
Во всех остальных случаях определение влияния стоек занимает немного больше времени, но главное помнить, что это влияние находится в указанных выше пределах.
Итак, в промежуточных стойках в результате сопротивления будет возникать изгибающий момент. Этот момент будет увеличивать значение момента для левого горизонтального элемента и уменьшать значение момента для правого горизонтального элемента, или наоборот - тут все будет зависеть от знака момента, действующего на стойку.
Принято считать, что если действие момента приводит к растяжению правой части сечения вертикальной стойки, то такой момент считается положительным, а если к растяжению левой части сечения, то отрицательным.
Другими словами, если мы повернем вертикальную стойку на 90 градусов по часовой стрелке, то получим горизонтальную балку, для которой знак момента определяется по тому же принципу. Так в балке момент считается положительным, если растяжение возникает в нижней части сечения, а отрицательным, если в верхней части сечения.
В итоге, если у простой неразрезной балки моменты на промежуточных опорах слева и справа от опоры равны, то в раме, рассматриваемой как балка, на опорах, соответствующих промежуточным вертикальным стойкам, моменты справа и слева от стойки могут быть не равны, а их разница и будет составлять значение момента Мв, действующего на промежуточную вертикальную стойку:
±Мв = Мгпр - Мглев (491.1)
или
Мгпр = Мглев ± Мв (491.2)
Это означает, что классическое уравнение трех моментов, применимое для неразрезной многопролетной балки, с учетом разности моментов на опорах примет несколько другой вид и станет уравнением 5 моментов. Так для n-ной опоры при одинаковой жесткости всех элементов:
Mn-1ln + 2Mлевnln + 2Мпрnln+1 ± 2Мвnlвn + Mn+1ln+1 = - 6φnEI (491.3)
Как мы знаем, при количестве пролетов k, количество составленных уравнений трех моментов составляет k-1. Этого достаточно, чтобы определить количество неизвестных моментов, составляющих k-1. Но как быть в этом случае? Ведь даже для двухпролетной балки, для которой можно составить всего лишь одно уравнение, количество неизвестных в этом уравнении будет равно 3. Что уж тут говорить, например, про 9-пролетную балку, для которой можно составить 8 уравнений, а в этих уравнениях будут 20 неизвестных величин.
На первый взгляд решение системы уравнений, составленных подобным образом, невозможно. Однако в строительной механике ничего невозможного нет, если рассмотреть возникшую проблему несколько иначе.
Дело в том, что нас никто не заставляет сразу определять угол поворота на рассматриваемой опоре многопролетной балки, как это следует из уравнения (491.3). Т.е. мы, воспользовавшись принципом суперпозиции, можем сначала определить эти углы поворота для простой неразрезной многопролетной балки (1 этап расчета), а затем рассматривать эти углы поворота - как фиктивные моменты M', действующие в местах крепления промежуточных вертикальных стоек к горизонтальным элементам (2 этап расчета). Это позволит определить моменты, действующие на промежуточные стойки, а также моменты слева и справа (3 этап расчета). Т.е. расчет производится не сразу, а как бы в 3 этапа. Таким образом действительное значение момента, действующего на горизонтальные элементы рамы, будет составлять:
М = М1э ± М2э; (491.4.1)
А значение момента, действующего на рассматриваемую стойку:
Мс = - 2M2э; (491.4.2)
Физический смысл формул (491.4) следующий:
1. Если угол поворота поперечного сечения в рассматриваемой точке отличен от нуля, то наличие вертикальной стойки приведет к уменьшению этого угла поворота.
2. Момент, определенный на 2 этапе, как раз и означает такое уменьшение угла поворота сечения.
3. Так как уменьшение угла поворота будет одинаковым и для левого и для правого горизонтального элементов, то и значения моментов 2 этапа для горизонтальных элементов будут иметь одинаковые значения, но разный знак (см. рис. 491.3).
4. Так как вертикальная стойка уменьшает углы поворота поперечных сечений двух горизонтальных элементов, то и расчетный момент для стойки будет равен двум моментам второго этапа. А знак "-" в данном случае означает, что при действии положительного фиктивного момента значение момента определенного на 2 этапе, будет отрицательным, и наоборот.
Если все элементы рамы имеют одинаковую длину, жесткость и условия закрпления, то расчетное значение момента для стойки можно определить по следующей формуле:
Мс = M' + M2э; (491.4.3)
Т.е. мы как бы прикладываем фиктивный момент к стойке, а затем учитываем общее изменение угла поворота в рассматриваемой точке.
Теперь, чтобы было более понятно, о чем идет речь, рассмотрим следующий простой пример.
Пример расчета простой симметричной рамы на несимметричную вертикальную нагрузку
Имеется простая симметричная рама, состоящая из одного вертикального элемента - стойки и двух горизонтальных элементов, которые можно рассматривать как балку. Размеры и жесткости стойки и балки одинаковые. Рама показана на рисунке 491.1:

Рисунок 491.1. Расчетная схема для простой симметричной рамы.
Если на раму будет действовать симметричная вертикальная нагрузка, то угол наклона поперечного сечения в точке В будет равен нулю и в этом случае даже никаких дополнительных расчетов не требуется. Мы же рассмотрим случай, когда только один пролет у рамы загружен, как это показано на рисунке 491.1.
1 этап: Расчет рамы как двухпролетной неразрезной балки
Определение изгибающего момента, действующего на опоре В, для двухпролетной неразрезной балки большого труда не составляет. Для этого достаточно составить одно уравнение:
2МB1э(l + l) = -6Rф (491.5.1)
Согласно таблицы 315.1 суммарная фиктивная реакция при действии равномерно распределенной нагрузки в одном пролете будет составлять:
Таблица 315.1.
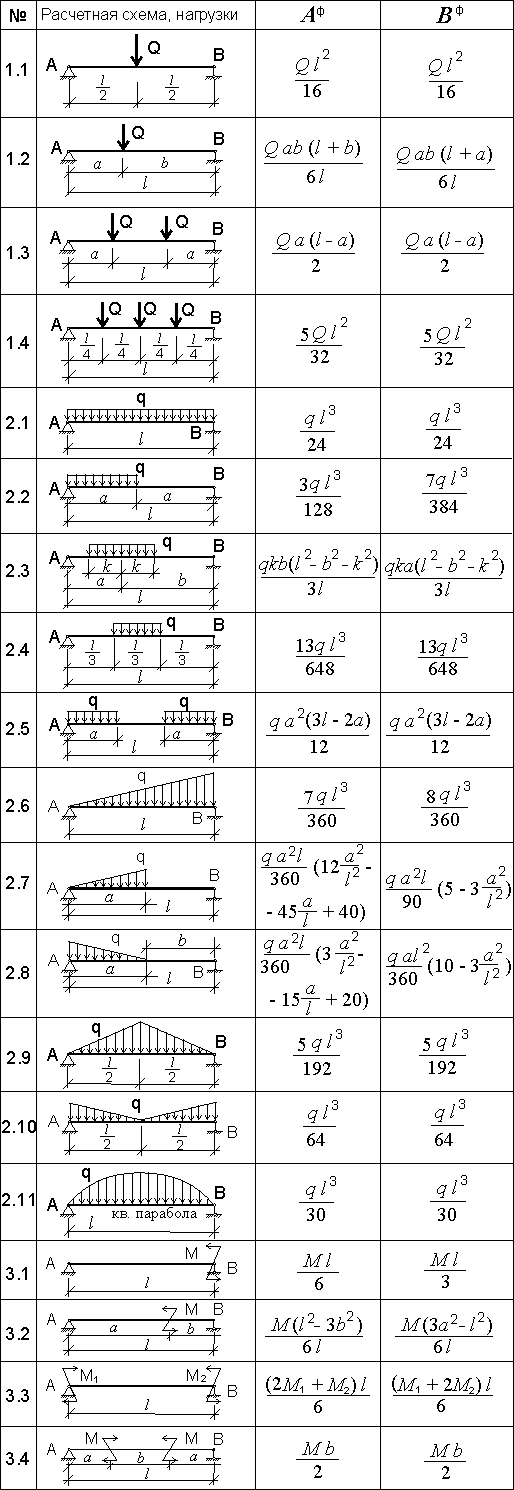
Rф = ql3/24 (491.5.2)
Тогда
4МВ1эl = -6ql3/24; MВ1э = -ql2/16 (491.6)
При этом угол наклона сечения в точке В будет составлять:
θпрВ = -ql3/24EI - MВl/3EI = - ql3/24EI + ql3/(3·16EI) = - ql3/48EI (491.7.1)
где -ql3/24EI - угол поворота на рассматриваемой опоре однопролетной шарнирной арки (именно это значение мы и подствляли в уравнения (491.5), MВ1эl/3EI - угол поворота в результате действия изгибающего момента в рассматриваемом узле.
Впрочем, если бы рассматривали левую часть неразрезной балки, на которую нагрузка не действует, то угол наклона поперечного сечения можно определить еще проще:
θлевВ = MВ1эl/3EI = -ql3/48EI (491.7.2)
И в первом и во втором случае знак "-" означает, что рассматриваемое поперечное сечение имеет наклон по часовой стрелке относительно оси z. Вот только направления моментов в первом и втором случае разные, поэтому и знаки моментов в уравнениях разные.
2 этап: Учет наличия вертикальной стойки
Так как вертикальная стойка у нас все-таки есть и угол поворота, согласно вычислений на первом этапе, не равен нулю, то наличие такой стойки следует учесть.
Если нам известен угол поворота сечения на одной из опор шарнирной однопролетной балки, то это и будет фиктивная опорная реакция на этой опоре при этом фиктивная реакция на соседней опоре будет в 2 раза меньше, так как угол поворота на соседней опоре в 2 раза меньше, чем на опоре, где приложен изгибающий момент.
Впрочем мы можем определить и момент, вызывающий такой угол поворота на данной опоре (назовем его фиктивным моментом), преобразовав соответствующим образом формулу (491.7.2). Тогда:
М' = -3θлевВ/l = -3ql3/48l = -ql2/16 (491.8.1)
Т.е. теперь мы кроме уже определенного ранее момента на опоре В дополнительно прикладываем в этой точке фиктивный момент М' и проверяем, как это влияет на стержни всей рамы.
Так как у нас в точке В сходятся 3 стержня, имеющие одинаковую длину, жесткость и условия закрепления, то и без всяких расчетов ясно, что момент распределится равномерно на все 3 стержня и таким образом МВ2э = ql2/(16·3) = ql2/48.
Кроме того, уравнение (491.4.2) означает, что мы можем условно рассечь раму так, чтобы одна половина стойки оказалась слева, а вторая справа, и рассматривать каждую из двух частей рамы отдельно:

Рисунок 491.2.
При таком рассечении жесткость рассматриваемых частей стойки уменьшится в 2 раза. Это означает что при приведении жесткости к одному значению, расчетная длина частей стойки увеличится в 2 раза и тогда, уравнение 3 моментов для левой части будет иметь следующий вид:
2МB2э(l + 2l) = -(-6M'Вl/3) = -6θBлев (491.9.1)
6МВ2эl = 6ql3/(3·16); MВ2э = ql2/48 (491.9.2)
Если же рассматривать правую часть рамы, то значение момента второго этапа будет таким же, но с обратным знаком, т.е. отрицательным. Рассмотрим опять раму в целом:

Рисунок 491.3.
Как видно из рисунка 491.2, действие момента, приложенного в точке В, будет приводить к изменению положения нейтральных осей элементов рамы. При этом нейтральная ось элемента АВ будет находиться под осью х, элемента ВС - над осью х, а элемента DB - справа от оси у. Это означает, что такой момент будет отрицательным для элемента ВС и положительным для элементов АВ и DB. А вообще особенности расчета конструкций на действие момента, приложенного на средней опоре, изложены отдельно.
3 этап: Определение расчетных моментов для всех элементов рамы
Таким образом уточненный момент на эпюре моментов в верху вертикальной стойки согласно формулы (491.4.3) составит:
МсВ = -ql2/16 + ql2/48 = -ql2/24 (491.10.1)
Впрочем, если мы определим значение момента для стойки по формуле (491.4.2), то оно будет таким же. Момент, действующий на неразрезную балку слева от опоры, составит:
МлевВ = -ql2/16 + ql2/48 = -ql2/24 (491.10.2)
А момент, действующий на неразрезную балку справа от опоры составит:
МпрВ = -ql2/16 - ql2/48 = -ql2/12 (491.10.3)
Проверка по площадям эпюр (4 этап)
На основании полученных данных мы можем определить опорные реакции, значения моментов в пролетах, а затем построить все необходимые эпюры: эпюру моментов, поперечных и продольных сил. Сделать это в принципе несложно, но в данном случае нас больше интересует эпюра моментов, на ней мы и остановимся. А для большей наглядности построим эпюры моментов сначала для однопролетной шарнирной балки, на которую действует равномерно распределенная нагрузка, затем эпюру моментов для двухпролетной неразрезной балки (1 этап расчета) и эпюру для рамы (2 этап расчета):

Рисунок 491.4. Эпюры моментов и площади эпюр моментов а)однопролетной балки на шарнирных опорах, б) двухпролетной балки, в) симметричной рамы
На рисунке 491.4 показаны не только эпюры моментов, но и указаны площади этих эпюр. Определены площади эпюр следующим образом:
Как мы знаем, площадь фигуры, описанной квадратичной параболой, будет составлять 2hl/3. В данном случае высотой является значение момента в пролете, а длиной - длина пролета. В случае а) имеется только одна геометрическая фигура и площадь ее равна
Sпар = (ql2/8)2l/3 = ql3/12 (491.11.1)
В случае б) мы имеем целых три геометрических фигуры и вроде бы для точных вычислений нужно знать значение максимального момента в пролете, а также расстояние от точки В до точки, в которой момент равен нулю. Относительно просто можно определить только площадь треугольника со сторонами АВ и ql2/16, она составит
Sтр = ql3/32 (491.11.2)
Но если мы присмотримся к эпюре моментов в случае б) внимательнее, то увидим, что площадь эпюр на участке ВС можно рассматривать, как разницу площадей параболы и треугольника
SBC = Sпар - Sтр = ql3/12 - ql3/32 (491.11.3)
Тогда суммарная площадь эпюры составит:
S"М" = Sтр + SBC = ql3/32 + ql3/12 - ql3/32 = ql3/12 = Sпар (491.11.4)
В случае в) высота треугольника на участке ВС, уменьшающего площадь фигуры, описанной параболой, равна сумме высот треугольников со сторонами АВ и ВD. Соответственно в итоге суммарная площадь эпюры не изменится.
Как видим во всех 3 случаях суммарные площади эпюр одинаковые и это является одним из вариантов проверки правильности расчетов.
Конечно же пользоваться этим методом проверки нужно очень осторожно. Так если рассматривать двухпролетную неразрезную балку с равными пролетами в которых действует равномерно распределенная нагрузка, как две отдельные балки с равными пролетами, то суммарная площадь эпюр для таких балок составит 2ql3/12 = ql3/6. Между тем суммарная площадь эпюр неразрезной балки будет в 4 раза меньше. Именно поэтому 1 неразрезная двухпролетная балка выгоднее, чем две однопролетных такого же сечения. Ведь площадь эпюр - это и есть показатель углов поворота. Т.е. в итоге углы поворота, а значит и прогибы в неразрезной балке будут значительно меньше. Впрочем, если бы к обеим горизонтальным элементам рамы была приложена симметричная нагрузка, то и начальная эпюра моментов имела бы другой вид.
Если стойка имеет нулевую длину
Как правило рамы с одинаковыми по длине и жесткости элементами и условиями закрепления на опорах - это частный случай, хотя и достаточно широко распространенный. Но сейчас мы рассмотрим другой частный случай, в действительности никогда не встречающийся, но теоретически возможный, а именно, когда стойка рассмотренной выше рамы имеет нулевую длину.
Вообще, если стойка имеет нулевую длину или бесконечно большую жесткость (что в принципе одно и то же), то и без всяких расчетов ясно, что такая стойка создает условия жесткого защемления на опоре В, в итоге угол поворота поперечного сечения на опоре В будет равен нулю. А значит:
МВправ = МсВ = -ql2/8 (494.12.1)
MВлев = 0 (494.12.2)
Если рассматривать отдельно левую или правую части рамы, рассеченной по стойке, то результат будет таким же:
2МB2э(l + 0) = -(-6M'Вl/3) = -6θBлев (491.13.1)
2МВ2эl = 6ql3/(3·16); MВ2э = ql2/16 (491.13.2)
Соответственно:
МсВ = - 2ql2/16 = - ql2/8 (491.14.1)
МлевВ = -ql2/16 + ql2/16 = 0 (491.14.2)
МпрВ = -ql2/16 - ql2/16 = -ql2/8 (491.14.3)
Если длина стойки в 2 раза меньше длины горизонтальных элементов
В этом случае при рассечении рамы приведенная длина стойки будет равна длине горизонтальных элементов и на 2 этапе расчета уравнение трех моментов для одной из частей рамы будет иметь следующий вид:
2МB2э(l + l) = -(-6M'Вl/3) = -6θBлев (491.15.1)
4МВ2эl = 6ql3/(3·16); MВ2э = ql2/32 (491.15.2)
Соответственно:
МсВ = - 2ql2/32 = - ql2/16 (491.15.3)
МлевВ = -ql2/16 + ql2/32 = -ql2/32 (491.15.4)
МпрВ = -ql2/16 - ql2/32 = -3ql2/32 (491.15.5)
Таким образом увеличение момента на 2 этапе составляет 24/16 = 1.5 раза или 50%.
Если длина стойки в 2 раза больше длины горизонтальных элементов
В этом случае при рассечении рамы приведенная длина стойки будет в 4 раза больше длины горизонтальных элементов и на 2 этапе расчета уравнение трех моментов для одной из частей рамы будет иметь следующий вид:
2МB2э(l + 4l) = -(-6M'Вl/3) = -6θBлев (491.16.1)
10МВ2эl = 6ql3/(3·16); MВ2э = ql2/80 (491.16.2)
Соответственно:
МсВ = - 2ql2/80 = - ql2/40 (491.16.3)
МлевВ = -ql2/16 + ql2/80 = -ql2/20 (491.16.4)
МпрВ = -ql2/16 - ql2/80 = -3ql2/40 (491.16.5)
Т.е. при таких условиях момент на 2 этапе составляет 24/40 = 0.6 от момента при равных длинах всех элементов или 60%.
Ну и в завершение темы рассмотрим еще один случай
Если стойка имеет жесткое защемление на конце
Согласно формуле (495.10) значение момента на втором этапе составит:
MВ2э = 4M'/10 = ql2/40 (491.11.1)
а уточненные моменты:
МсВ = - 2ql2/40 = -ql2/20 (491.12.1)
МлевВ = -ql2/16 + ql2/40 = -3ql2/80 (491.12.2)
МпрВ = -ql2/16 - ql2/47 = -7ql2/80 ≈ ql2/11.43 (491.12.3)
Отсюда мы можем сделать вывод, что влияние жесткого защемления внизу стойки на значение моментов для горизонтальных элементов будет крайне незначительным. При этом относительное увеличение момента справа от стойки составит: 7·12/80 - 1 = 5%. А относительное увеличение момента для стойки: 24/20 - 1 = 20%.
А теперь посмотрим как наличие промежуточных вертикальных стоек влияет на расчет рам с достаточно большим количеством пролетов.
Пример расчета простой трехпролетной рамы с шарнирными опорами
Имеется рама, состоящая из 3 горизонтальных и 4 вертикальных элементов. На горизонтальные элементы рамы действует вертикальная равномерно распределенная нагрузка q.

Рисунок 491.5. Расчетная схема для простой трехпролетной рамы.
1 этап
На этом этапе расчета такую раму можно рассматривать как неразрезную балку с 5 пролетами, равными по длине. Необходимо составить 4 уравнения трех моментов, но так как рама и нагрузка являются симметричными, т.е. MB = ME и МС = МD, то достаточно составить 2 уравнения:
2MB1э(2l) + MC1эl = - 6·Rф1; (491.12.1)
MB1эl + 2MC1э(2l) + МD1эl = - 6·Rф2; (491.12.2)
где
Rф1 = АBф = ql3/24 (491.12.3)
Rф2 = ВCф + АDф = ql3/12 (491.12.4)
Тогда
2MB1э(2l) + MC1эl = - ql3/4; (491.12.5)
MB1эl + 2MC1э(2l) + МD1эl = - ql3/2; (491.12.6)
4MB1эl = - ql3/4 - MC1эl; МВ1э = -ql2/16 - MC1э/4 (491.13.1)
-ql3/16 - MC1эl/4 + 4MC1эl + МC1эl = - ql3/2; 19MC1эl/4 = -7ql3/16 (491.13.2)
Тогда
МС1э = MD1э = - 7ql2/76 ≈ - ql2/10.85; MB1э = ME1э = -ql2/16 + 7ql2/304 = - 12ql2/304 = -3ql2/76 ≈ - ql2/25.33 (491.14)
При этом угол наклона в точке C будет составлять:
θпрC = -ql3/24EI - MC1эl/3EI - MD1эl/6EI = - ql3/24EI + 7ql3/(3·76EI) + 7ql3/(6·76EI) = ql3/228EI (491.15)
Такой угол наклона поперечного сечения является относительно небольшим и даже без дальнейших расчетов ясно, что сильно промежуточные стойки на окончательный результат не повлияют. Поэтому для упрощения расчетов значение момента на 2 этапе расчета можно принять равным М2э = ql2/228.
Тем не менее продолжим.
Положительное значение угла поворота в начале рассматриваемого пролета показывает, что растягивающие напряжения будут возникать в правой части сечения стойки CC'. При определении угла наклона в точке D мы получили бы точно такой же результат, но с обратным знаком, что означает возникновение растягивающих напряжений в левой части сечения стойки DD'. Таким образом для дальнейших расчетов мы можем заменить промежуточные на положительные моменты, приложенные в точках С и D. M'C = M'D = 3ql3/228l = ql2/76.
2 этап
Как мы выяснили, определение момента на 2 этапе будет достаточно простым, если у рамы всего 3 стержня, при этом одинаковая длина, жесткость элементов и условия закрепления. Тогда значение момента МС на втором этапе составило бы МС2э = -ql2/(76·3) = -ql2/228 для всех элементов в точке С. Но в нашей раме 7 стержней и действие фиктивного момента будет распространяться на все 7 стержней, хотя и с разной долей эффективности. К тому же фиктивный момент приложен к двум стойкам. Т.е. для одних стержней (для левого горизонтального элемента и стойки в точке С) значение момента на втором этапе будет больше, а для других (правого горизонтального элемента в точке С) - меньше.
Если мы не будем обращать на это внимания и составим уравнения трех моментов, то можем определить значение момента на втором этапе для одного из трех стержней.
2MB2э(2l) + MC2эl = 0 (491.16.1)
MB2эl + 2MC2э(3l) + МD2э(2l) = - 6·RфС; (491.16.2)
где фиктивная опорная реакция в точке В слева равна нулю, так как мы прикладываем моменты (для упрощения расчетов) чуть правее точки С и чуть левее точки D (другими словами мы рассекаем раму так, что обе стойки попадают в среднее сечение). Это также означает, что сами по себе эти моменты первого уравнения поворота на опоре С не создают, а являются лишь следствием момента, заменяющего стойку. Другими словами, каково бы ни было значение момента в точке С, значение момента в точке В в данном случае будет в 4 раза меньше и будет иметь обратный знак. Соответственно фиктивная опорная реакция для второго уравнения согласно расчетной схеме 3.3, таблицы 315.1 составит:
RфС = ВCф + АDф = 3M'l/6 = ql3/(76·2) = ql3/152 (491.16.3)
Тогда
4MB2эl = - MC2эl; MB2э = - MC2э/4 (491.16.4)
- MC2эl/4 + 6MC2эl + 2МC2эl = - 6ql3/152; 31MC2эl/4 = -6ql3/152 (491.16.5)
МС2э = MD2э = - 3ql2/589; MB2э = ME2э = 3ql2/(589·4) = 3ql2/2356 (491.17)
Судя по знаку - это МСлев2э. Тогда уточненное значение момента слева от стойки СС' составит:
МлевC = -7ql2/76 - 3ql2/589 = -4351ql2/44764 ≈ -ql2/10.29 (491.18.2)
Т.е. в итоге максимальное изменение значения момента составит 10.85/10.29 = 1.055 раза или 5.5% (где 10.85 и 10.29 - знаменатели значений моментов первого и второго этапа).
В целом, для того, чтобы узнать значение МСправ2э, нужно рассматривать влияние каждой стойки отдельно, т.е. составить и решить 2 системы из 4 уравнений, так как в данном случае нагрузка будет несимметричной, причем уравнения нужно составлять очень внимательно. Затем на основании решения 2 систем уравнений построить эпюры моментов отдельно для каждого фиктивного момента, затем суммарную эпюру и уже по этой суммарной эпюре можно определить значения моментов 2 этапа. В итоге мы узнаем, что МСправ2э будет немного меньше (примерно на 1/6), чем -МСлев2э.
Вот только, на мой взгляд, в данном случае в этом нет совершенно никакой необходимости. Тем более, когда речь идет о расчете рамы, которая будет выполнена в единственном экземпляре.
Достаточно и того, что мы определили максимально возможное изменение момента для левого горизонтального элемента. Для упрощения расчетов и повышения надежности рамы изменение момента МСправ2э вообще можно не учитывать, тогда
3 этап
Уточненные значения моментов для рассматриваемых элементов рамы составят:
МсС = - 2·3ql2/589 ≈ -ql2/98.2 (491.18.1)
МлевС ≈ -ql2/10.29 (491.18.2)
МпрС = МС1э ≈ ql2/10.85 (491.12.3)
Более того, и для стойки можно принять большее значение расчетного момента, например, равным фиктивному моменту с обратным знаком -М'С = -ql2/76. Еще более того, для правого горизонтального элемента мы для большей надежности можем не просто оставить так как есть значение первого этапа расчетов, а и увеличить его на значение момента второго этапа, в итоге МлевС = МпрС.
У механиков есть такое неписанное правило: чем проще система (т.е. чем меньше в ней деталей и узлов сопряжения), тем она надежнее. Это же можно сказать и о расчетах: чем проще расчет, тем он надежнее.
Например, при расчетах на втором этапе мы где-то ошиблись со знаками (при таком обилии данных это бывает), в результате значения моментов справа и слева от промежуточных стоек поменяются местами. Между тем, если задаться соответствующим коэффициентом надежности по нагрузке, учитывающим возможные изменения момента при наличии вертикальных стоек и просто умножить значения момента первого этапа на этот коэффициент, то возможное влияние указанной ошибки, как и других возможных ошибок будет нивелировано, а кроме того сам расчет значительно упростится.
Более того, чем больше пролетов в раме, тем меньше будет в итоге влияние промежуточных стоек. Ведь при этом углы наклона поперечных сечений на промежуточных опорах будут стремиться к нулю, а значения моментов на промежуточных опорах будут стремиться к -ql2/12, а значит и балки в таких пролетах все больше будут подходить под определение балки с жестко защемленными опорами, у которых угол поворота поперечного сечения на опорах равен нулю. Так что для таких рам даже без первого этапа расчетов можно обойтись, если использовать соответствующий коэффициент надежности и учитывать то, что моменты для горизонтальных элементов в крайних пролетах будут отличаться от моментов в промежуточных пролетах. В итоге чем более сложной изначально является рама, тем более простым может оказаться расчет, как ни парадоксально это звучит.
Общий вывод: Для упрощения расчетов многопролетных простых рам влиянием промежуточных стоек на изменение угла поворота горизонтальных элементов можно пренебречь, задавшись соответствующим дополнительным коэффициентом надежности по нагрузке, учитывающим возможное изменение момента γнм.
А вот какое именно лучше принять значение коэффициента надежности по нагрузке, зависит от множества факторов, частично мы их рассмотрели в 1 примере расчета.
Возможные значения коэффициентов надежности по нагрузке при упрощенном расчете рам
1. Рамы, элементы которых имеют одинаковую длину, жесткость и условия закрепления на опорах.
1.1. Для однопролетной рамы определять дополнительный коэффициент надежности по нагрузке нет необходимости, так как можно сразу воспользоваться результатами расчета такой рамы.
1.2. Для двухпролетной рамы при действии равномерно распределенной нагрузки в обеих пролетах определять дополнительный коэффициент надежности по нагрузке также нет необходимости, так как угол поворота на промежуточной опоре будет равен нулю.
1.3. Для трехпролетной рамы, как мы выяснили выше, дополнительный коэффициент нагрузки можно определить следующим образом. Так как максимальное изменение момента составляет 5.5%, то γнм1.3 = 1 + 0.055 = 1.055.
1.4. Для рам с 4 пролетами значение дополнительного коэффициента надежности по нагрузке согласно формуле (493.6) может составлять γнм1.4 = 1.04.
1.5. Для рам с 5 и более пролетами значение дополнительного коэффициента надежности по нагрузке будет еще меньше. При расчете таких рам можно пользоваться γнм1.5 = 1.04.
2. Рамы, элементы которых имеют разную длину и жесткость, или разные условия закрепления на опорах.
2.1 Если у стоек снизу не шарнирная опора, а жесткое защемление, то это, как мы уже выяснили, приведет к увеличению расчетного момента второго этапа в 1.2 раза. Таким образом значение коэффициента составит γнм2.1 = 1 + 0.055·1.2 = 1.067.
2.2. Если длина стоек в 2 раза меньше длин горизонтальных элементов или жесткость стоек в 2 раза больше, чем горизонтальных элементов, то это также приведет к увеличению расчетного момента, принимаемого на 2 этапе, Максимальное изменение, как мы выяснили будет составлять 1.5 раза. Соответственно в этом случае для упрощения расчетов можно принимать коэффициент γнм2.2 = 1 + 0.055·1.5 = 1.083.
2.3. Если длина стоек в 2 раза больше длин горизонтальных элементов или жесткость стоек в 2 раза меньше, чем горизонтальных элементов, то это приведет к уменьшению расчетного момента, принимаемого на 2 этапе, Максимальное изменение, как мы выяснили будет составлять 0.6 раза. Соответственно в этом случае для упрощения расчетов можно принимать коэффициент γнм2.2 = 1 + 0.055·0.6 = 1.033.
2.4. Если все стойки имеют длину, близкую к нулевой, или жесткость, близкую к бесконечной. То все горизонтальные элементы рамы рассчитываются как жестко защемленные рамы на обеих опорах. Никаких дополнительных коэффициентов при этом не требуется.
2.5. Если стойки имеют длину, близкую к бесконечной или жесткость близкую к нулевой, то никакого влияния такие стойки на горизонтальные элементы рамы не оказывают и их можно рассчитывать как простую неразрезную балку. Никаких дополнительных коэффициентов при этом не требуется.
Примечание: При промежуточном значении длин и(или) жесткостей значение дополнительного коэффициента можно определить интерполяцией.
3. Если у многопролетной рамы одноэтажного здания горизонтальные элементы будут сверху и снизу, образуя замкнутые контуры, и при этом опирание внизу остается шарнирное, то при одинаковой вертикальной нагрузке на верхние и на нижние горизонтальные элементы, при одинаковой жесткости и длине элементов расчетная длина промежуточных стоек в результате деформации уменьшится в 2 раза. Т.е. в этом случае можно принимать коэффициент γнм3 = γнм2.2 = 1.0.83.
4. 1. Для рам многоэтажных зданий, горизонтальные элементы которых загружены одинаковой равномерно распределенной нагрузкой, кроме того соблюдаются условия п.3, коэффициент γнм4.1 = γнм2.2 = 1.083
4.2. Если у рамы многоэтажного здания нижние стойки имеют жесткое защемление и соответственно горизонтальные элементы на уровне низа стоек отсутствуют, то в этом случае значение коэффициента можно принимать в пределах γнм4.2 = 1.067÷1.083.
В целом, как я уже говорил в начале, практически для любой плоской рамы при расчете на вертикальную равномерно распределенную нагрузку можно принимать дополнительный коэффициент надежности по нагрузке 1.1, а если колонны рамы будут иметь меньшую длину и жесткость чем горизонтальные элементы, а так оно чаще всего и бывает, то достаточно и коэффициента 1.05. | 
