Вообще-то ответы на первую часть вопроса, относящуюся к балкам, даны достаточно подробно (и именно на пальцах) в статьях "Основы сопромата", "Основы сопромата, расчетные формулы", "Моменты инерции поперечного сечения" и других. А для тех, кого смущает такое обилие информации, я и написал данную статью. Вторая часть вопроса возникает из-за того, что люди путают расчет изгибаемых и сжимаемых элементов (расчет на поперечный и продольный изгиб).
Сначала отвечу коротко:
При расчете балок принимается момент инерции Iz, если нагрузка к балке приложена в плоскости ху:
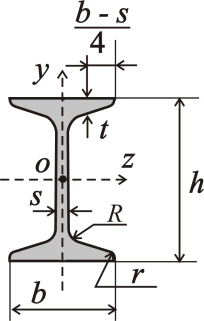
Рисунок 497.1.
т.е. если балка расположена в пространстве так, что ее поперечное сечение соответствует показанному на рисунке 497.1, и к балке приложена вертикальная нагрузка, то расчетный момент инерции - Iz. Если же пространственное положение балки таково, что поперечное сечение соответствует показанному на рисунке 497.1, но при этом повернутому на 90°, то вертикальная нагрузка на такую балку будет действовать в плоскости xz, соответственно расчетным моментом будет Iy.
Ось х проходит через центр тяжести сечения О (на рисунке 497.1 не показана). Плоскость ху проходит через оси х и у, плоскость xz - через оси х и z.
Для сжатых элементов (колонн, стоек и т.п.) при всех прочих равных условиях расчетным является момент инерции с наименьшим значением.
А теперь более полный ответ, в основном состоящий из цитат по поводу физического смысла момента инерции:
Момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.
И тут может возникнуть вопрос, какое отношение все эти законы динамики и кинематики имеют к расчету статических строительных конструкций? Оказывается, что ни на есть самое прямое и непосредственное.
При решении определенных задач может рассматриваться не все тело, а только его поперечное сечение, а при необходимости несколько поперечных сечений. Но в этих сечениях действуют такие же физические силы, правда имеющие несколько иную природу. Таким образом, если рассматривать некое тело, длина которого постоянна, а само тело является однородным, то если не учитывать постоянные параметры - длину и плотность (l = const, ρ = const) - мы получим модель поперечного сечения.
И последняя:
Среди осей прямоугольной системы координат, проходящих через центр тяжести поперечного сечения, есть две взаимно-перпендикулярные оси, относительно которых осевые моменты инерции принимают максимальное и минимальное значение, при этом центробежный момент инерции сечения Izy = 0. Такие оси называют главными центральными осями поперечного сечения, а моменты инерции относительно таких осей – главными центральными моментами инерции.
На моем сайте для главных центральных осей принято обозначение z и у, соответственно главные центральные моменты инерции обозначаются как Iz и Iy. В некоторых справочниках приняты оси х и у, соответственно даются значения Ix и Iy, но принципиального значения это не имеет, так как изменение обозначения ни физический смысл ни значение момента инерции не изменяет.
Соответственно для балок, рассчитываемых на вертикальную нагрузку, определяющим является положение поперечного сечения. А для для сжатых стержней - характер закрепления на опорах и точка приложения нагрузки.
Т.е. нагрузка к сжимаемому стержню может быть приложена не только по центру тяжести сечения, но и с эксцентриситетом в одной или в обеих плоскостях. Опоры стержня в различных плоскостях также могут быть разными и потому расчет таких стержней должен производиться с учетом этих особенностей. Если к балке вертикальная нагрузка приложена с эксцентриситетом, превышающим половину ширины балки, то такую балку следует дополнительно рассчитывать на действие крутящего момента. |

