Cодержание:
Основы сопромата кратко.
1. Виды опор.
1.1. Шарнирные опоры.
Расчетная длина (пролет) балки.
1.2. Опорные связи шарнирно закрепленной балки.
1.3 Жесткое защемление на опорах.
1.4. Скользящие заделки.
2. Нагрузки (внешние силы).
3. Напряжения (внутренние силы).
4. Реакции опор.
5. Уравнения статического равновесия.
4.1. Определение опорных реакций.
6. Уравнения изгибающего момента.
7. Балка на двух шарнирных опорах.
8. Консольная балка.
9. Метод сечений.
10. Определение момента сопротивления.
11. Определение угла поворота.
12. Определение прогиба.
13. Определение угла поворота через прогиб.
14. Список использованной литературы.
10. Определение момента сопротивления.
(вернуться к основному содержанию)
Помнится, в школе нам рассказывали сказку: Пришло время отцу умирать, позвал он сыновей (а сыновей было много) и говорит, вон в углу стоит веник, ну-ка, старший сын, вытащи прутик из веника и попробуй его сломать. Вытащил старший сын прутик из веника и легко его сломал, то же самое проделали и остальные сыновья. А теперь сходите на кухню за новым веником, говорит отец, и попробуйте его сломать. Принесли сыновья новый веник ломали его, ломали, но так и не сломали. И тогда отец это простое с точки зрения теории сопротивления материалов событие истолковал так: видите дети, веник - это вы, если будете держаться вместе, никто вас не сломает, а если будете держаться поодиночке, то вас сломает кто угодно. Вообще-то отцу следовало на этом примере объяснить, что чем больше суммарная площадь прутков, на которые действует одна и та же нагрузка, тем меньше внутренние напряжения, возникающие в поперечном сечении веника, но не будем придираться к умирающему человеку, тем более, что он хотел только добра.
Для абсолютного большинства строительных материалов значение расчетного сопротивления уже определено эмпирическим путем, поэтому определить параметры сечения, на которое действуют растягивающие или сжимающие напряжения, не сложно. Значения расчетных сопротивлений для большинства строительных материалов есть в разного рода справочниках, тем не менее при большом желании эти значения можно определить и самому.
Пример №1. На поперечное сечение балки действует равномерно распределенная нагрузка, при этом сжимающие напряжения, возникающие в поперечном сечении балки, будут постоянными по всей высоте балки и в этом самом простом случае эти напряжения можно изобразить в виде такой же равномерно распределенной реакции , то же самое справедливо и для сосредоточенной нагрузки:
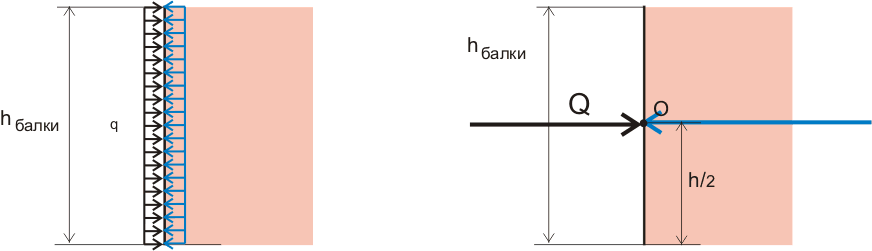
Рисунок 10.1. Внутренние напряжения в поперечном сечении балки.
В этом случае, если нам известна нагрузка и расчетное сопротивление материала, то можно легко определить площадь сечения конструкции:
S ≥ Q / R (10.1)
Пример №2. На поперечное сечение балки действует изгибающий момент, который можно заменить парой сил (рисунок 8.2) или распределенной нагрузкой, изменяющейся по высоте (рисунок 8.3). Т.е. растягивающие и сжимающие нормальные напряжения изменяются по высоте балки и поэтому использовать приведенную выше формулу нельзя, нужно как-то учитывать изменение внутренних напряжений в зависимости от высоты балки.
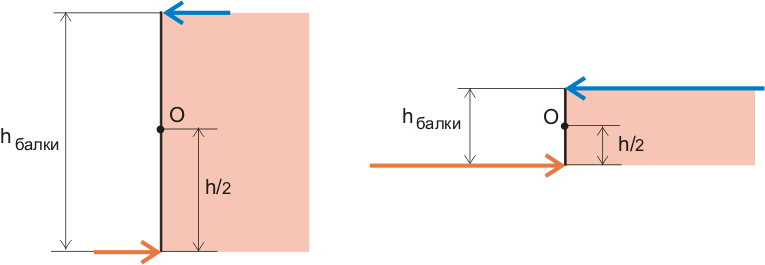
Рисунок 8.2. Увеличение значения сил при уменьшении высоты балки при одинаковом вращающем моменте.
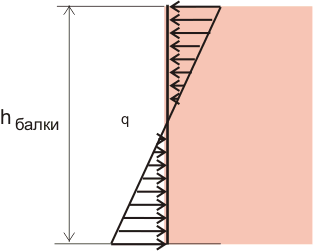
Рисунок 8.3. Изменение распределенной нагрузки по высоте балки.
Для наглядности на пару минут вернемся к нашей линейке. Если мы возьмем линейку, которая лежала на книгах плашмя, поставим ее и приложим к линейке точно такую же нагрузку как и к лежащей плашмя линейке, то линейка вообще не прогнется, точнее прогнется, но увидеть это невооруженным глазом невозможно. В чем же дело? ведь ни нагрузка, ни длина балки и, соответственно, изгибающий момент, ни материал балки, ни сечение балки не изменились, изменилось только положение балки в пространстве. Теория сопротивления материалов объясняет это чудо так: при действии на балку нагрузки балка деформируется (прогибается), при этом верхняя часть балки сжимается и в этой части возникают сжимающие напряжения, а нижняя часть балки растягивается и в этой части возникают растягивающие напряжения. Эти напряжения называются нормальными, так как они направлены перпендикулярно поперечному сечению балки (по нормали).
Конечно же при деформации балки в любом поперечном сечении возникают и касательные напряжения, направленные параллельно поперечному сечению (значение этих напряжений можно определить по эпюре "Q", рисунки 7.1 и 7.2), однако значение касательных напряжений при простом загружении в сечении, где действует максимальный изгибающий момент, равно нулю. При этом предполагается, что в некоторой точке (а точнее в ряде точек, которые находятся на оси z) поперечного сечения балки никаких деформаций нет, т.е. значение нормальных сжимающих или растягивающих напряжений равно 0, при этом максимальные сжимающие напряжения возникают в самом верхнем слое балки, а максимальные растягивающие напряжения возникают в самом нижнем слое балки. Графически это выглядит так:
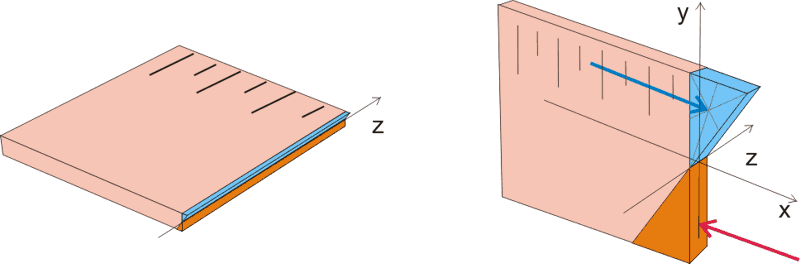
Рисунок 10.2. Напряжения, возникающие в поперечном сечении балки при действии изгибающего момента.
Примечание: как видно из этого рисунка, нормальные напряжения - это ответная реакция деформируемого материала на действующую пару сил или изгибающий момент.
Когда мы прикладывали пару сил к поперечному сечению балки (рисунок 8.2), то не сильно заботились о точках приложения сил. Теперь мы видим, что под действием этой пары сил в поперечном сечении балки возникают сжимающие и растягивающие напряжения и если рассматривать поперечное сечение балки, как отдельную балку, то сжимающие и растягивающие напряжения можно рассматривать как нагрузку, действующую на балку, а пару сил, создающую вращающий момент, в этом случае можно рассматривать, как реакции опор. Для того, чтобы соблюдалось условие равновесия системы, эти силы должны быть приложены не абы как, а на некотором вполне определенном расстоянии от точки "о" - центра тяжести сечения. И получается, что эти расстояния и есть плечи действующих сил, создающих момент опорных реакций.
Этот момент называется моментом сопротивления и обозначается как W. Таким образом момент сопротивления - это ответ материала на действие изгибающего момента.
Так как мы предполагаем для конструкции из однородного материала, что растягивающие напряжения суммарно равны сжимающим напряжениям и при этом площадь на которую действуют растягивающие напряжения, равна площади, на которую действуют сжимающие напряжения. То определить значение момента сопротивления мы можем следующим образом. Сначала сведем линейно-изменяющиеся нормальные напряжения к равнодействующим, обозначим их как Р:
Рσс = Рσр = P = (bh/2)σ/2 = bhσ/4 (10.2)
где b - ширина балки, h - высота балки, σ/2 - среднее значение нормальных напряжений, линейно изменяющихся от максимума σ до 0.
Тогда момент сопротивления для двух равнодействующих сил, действующих относительно центра тяжести сечения, составит:
W' = 2Py (10.3)
Теперь нужно определить у - плечо действия равнодействующих сил. Сделать это можно разными способами, мы воспользуемся самым простым и наглядным.
Как известно на все тела, живые и неживые, в пределах планеты Земля действует сила тяжести. Например, если линейка которую мы все никак не можем доломать, весит 50 г, то это означает, что на линейку действует сила тяжести 0.5 Н или 0.05 кгс. Кроме того, пока никто не опровергнул и предположения, что на каждый отдельный атом, молекулу и любую другую часть материи действует своя сила тяжести, при этом общая сила тяжести линейки равна сумме сил тяжести всех атомов или других частиц, входящих в состав этой линейки. Далее, чтобы линейка не падала на землю под воздействием силы тяжести, мы должны сделать опору для линейки хотя бы в одной точке. Точка эта не простая, получается, что сумма моментов, возникающих при действии сил тяжести, действующих на каждую частицу линейки, в этой точке равна нулю. Таким образом соблюдается условие равновесия системы. Вполне логично эта точка называется центром тяжести. Например, для нашей линейки центр тяжести находится в геометрическом центре линейки. Но сейчас нас интересует центр тяжести не прямоугольника, а треугольника, который символизирует внутренние напряжения или линейно изменяющуюся равномерную нагрузку. Как утверждает наука геометрия, центр тяжести треугольника находится на пересечении медиан углов треугольника, при этом расстояние от любого острого угла до высоты, опущенной на катет, равно 2/3 длины этого катета (рисунок 8.2). Так как мы рассматриваем не все поперечное сечение балки, а только верхнюю (или нижнюю половину), то
у = (h/2)(2/3) = h/3 (10.4)
Теперь, когда мы определили значение плеча силы, мы можем подставить его в формулу (4.3) и определить момент сопротивления для нашей балки прямоугольного сечения относительно оси z:
W'z = 2(bhσ/4)h/3 = σbh2/6 (10.5)
Примечание: как правило момент сопротивления рассматривается как геометрическая характеристика сечения. Т.е. нормальные напряжения в формуле опускаются (Wz = W'z/σ). Почему, мы узнаем чуть позже.
Момент сопротивления сечения можно определять и как отношение момента инерции относительно оси z к максимальному расстоянию от оси z до наиболее удаленных точек сечения.
Wz = Iz / (h/2) = (bh3 /12)/(h/2) = bh2/6 (10.6)
Что такое момент инерции, рассказывается отдельно. Здесь добавлю только, что момент сопротивления - это производная от момента инерции. Формулы для определения момента инерции и момента сопротивления для поперечных сечений различных геометрических форм также выложены отдельно.
Итак, в ходе долгих, хотя и не сложных вычислений мы определили, что
М = W' или M/W' = 1 или Мσ/W = σ (10.7)
А так как внутренние нормальные напряжения σ должны быть меньше или в крайнем случае равны расчетному сопротивлению материала (σ ≤ R), то формула (4.7) будет иметь несколько иной вид:
М/W = Mσ/W' ≤ R или W ≥ M/R (10.8)
Ну а теперь, когда мы уже столько всего знаем, то для проверки своих знаний определим момент сопротивления линейки в разных положениях. Когда линейка у нас лежала плашмя, то ширина балки была, например, 3 см, а высота 0.4 см, это значит, что момент сопротивления был 3·0.42 /6 = 0.48 см3. Когда мы поставили линейку, ширина балки составила 0.4 см, а высота 3 см и в этом случае момент сопротивления стал равен 0.4·32 / 6 = 3.6 см3, т.е. в 7.5 раз больше. Разница существенная.
Но это еще далеко не все, расчетные формулы сопромата позволяют достаточно легко определить не только касательные и нормальные напряжения, действующие на поперечное сечение балки, но также угол поворота и прогиб - перемещение центра тяжести поперечного сечения балки относительно оси у в любой точке.
(вернуться к основному содержанию) | 
