Для начала следует уяснить себе главный смысл теории сопротивления материалов:
Напряжения p в любой рассматриваемой точке должны быть меньше расчетного сопротивления материала R:
p < R (524.1)
Не смотря на кажущуюся простоту, это и есть самая главная и важная формула теории сопротивления материалов. Все остальное - частности и детали, рассмотрением которых мы ниже и займемся. Итак.
Расчет строительных конструкций выполняется с использованием метода сечений, который мы достаточно подробно рассматривали при выводе формул для расчета балок при изгибе.
Суть данного метода сводится к тому, что для определения напряжений в любом рассматриваемом сечении мы отсекаем часть конструкции, в общем случае - часть некоего физического тела, а для того, чтобы система находилась в статическом равновесии, заменяем отсеченную часть конструкции внешними силами. Соответственно напряжения в рассматриваемом сечении равны по значению внешним силам и направлены противоположно.
Тут следует добавить, что нагрузки, действующие на строительную конструкцию, опорные реакции, возникающие в результате действия нагрузок, а также силы, прикладываемые к поперечному сечению для того, чтобы система оставалась в состоянии статического равновесия, являются для рассматриваемой конструкции внешними силами. При этом внутренние силы, возникающие как реакция на действие внешних сил, называются напряжениями (которые впрочем также можно рассматривать как внешние силы).
В общем случае метод сечений и напряжения, действующие в рассматриваемом сечении и в частности в точке А, выглядят так:
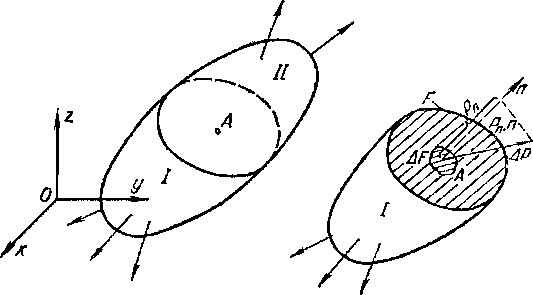
Рисунок 317.1
Т.е. в общем случае напряжения p могут быть направлены под углом, отличным от 90° по отношению к рассматриваемому сечению.
Все остальное следует из определений теории сопротивления материалов. Нормальные напряжения направлены перпендикулярно рассматриваемому сечению (по нормали). Касательные напряжения действуют в плоскости рассматриваемого сечения (потому и касательные).
Другими словами, если напряжения направлены под некоторым углом к плоскости рассматриваемого сечения, отличным от 90°, то мы, воспользовавшись законами геометрии, такой вектор всегда можем разложить на вертикальную (нормальные напряжения σn) и горизонтальную составляющие (касательные напряжения тn).
 (317.2) (317.2)
 (317.3) (317.3)
где n - ось, перпендикулярная рассматриваемому сечению (см.рис.317.1)
Однако сейчас нас интересует не общий случай, а вполне конкретный, а именно линейное напряженное состояние, т.е. такое состояние, когда только на двух главных площадках из шести действуют нормальные напряжения.
С подобной ситуацией мы сталкивались при расчете стержня на растяжение. Другими словами, центрально растянутый стержень можно условно считать находящимся в линейном напряженном состоянии (почему условно, об этом чуть позже).
В общем ситуация с расчетом стержня на растяжение выглядела так:

Рисунок 525.1. Нормальные напряжения при растяжении прямолинейного стержня.
Если мы представим, что на рисунке 525.1.г) изображен не стержень некоторой длины l (измеряется по оси х), ширины b (измеряется по оси z) и высоты h (измеряется по оси у), а некий элементарный параллелепипед, вырезанный из этого стержня со сторонами dx, dz и dy, при этом поверхности параллелепипеда параллельны поверхностям стержня, то мы получим достаточно наглядное представление о главных площадках напряжений. Одна из таких площадок показана на рисунке оранжевым цветом.
Главными площадками напряжений при любом напряженном состоянии называются такие площадки, на которые действуют максимальные нормальные напряжения (соответственно такие напряжения называются главными нормальными напряжениями), при этом касательные напряжения на главных площадках равны нулю.
Позвольте, скажете вы, но ведь нас не интересуют нормальные напряжения, действующие на какие-то площадки, пусть даже и элементарно малые. Нас интересует напряжение, например, в точке А (рис.317.1).
Все верно, нас интересуют напряжения в самой нагруженной точке сечения. Вот только нельзя забывать, что эту точку А мы выбираем на поверхности рассматриваемого сечения, а точка по умолчанию никакой направленности и площади сечения, на которую действуют напряжения, не имеет. Поэтому любые напряжения, действующие в этой точке будут условно говоря нормальными по отношению к точке, к тому же эти напряжения более правильно рассматривать как сосредоточенные силы.
А вот параллелепипед, пусть даже и элементарно малый и даже своими размерами сопоставимый с точкой, уже имеет плоские поверхности, а эти поверхности имеют некоторую площадь, пусть даже и элементарно малую ΔF. А элементарно малый параллелепипед (в идеале куб) со сторонами dx→0, dz→0, dy→0 нам нужен для того, чтобы не учитывать возможное изменение напряжений по длине (или другому параметру) стержня (пример изменения нормальных напряжений по длине и по высоте изгибаемой балки на шарнирных опорах можно видеть на рисунке 145.8).

Рисунок 145.8.
Таким образом, рассматривая элементарный параллелепипед, мы допускаем, что нормальные напряжения на параллельных площадках равны (и направлены в противоположные стороны), соответственно никаких дополнительных внешних сил на параллелепипед не действует, кроме того, эти напряжения равномерно распределены по поверхности рассматриваемых площадок (являются плоской равномерно распределенной нагрузкой) и это значительно упрощает рассмотрение данного параллелепипеда.
Но это еще далеко не все. Рассматриваемое нами до этого поперечное сечение, т.е. перпендикулярное нейтральной оси стержня - это частный случай. В общем случае сечение может иметь угол наклона, отличный от 90°, причем не только в одной, но и в двух плоскостях. Зачем нужно усложнять такую вроде бы простую и понятную задачу по определению нормальных напряжений, мы узнаем чуть позже, а пока рассмотрим следующую ситуацию:

Рисунок 524.1. Действие напряжений на наклонных площадках
До этого мы рассматривали поперечное сечение стержня (на рисунке 524.1 это сечение перпендикулярно оси х) и даже определили для него значение нормальных напряжений (σ = N/F). Если рассматривать сечение наклоненное к оси у под некоторым углом α, то в этом сечении также будут действовать напряжения р, однако значение этих напряжений будет меньше, так как из-за наклона площадь сечения увеличится. В целом, вне зависимости от значения угла наклона, всегда будет соблюдаться равенство:
N = σF = pFα (524.1)
где F - площадь поперечного сечения, Fα - площадь наклонного сечения.
Так как площадь наклонного сечения зависит от угла наклона:
Fα = F/cosα или F = Fαcosα (524.2)
то, подставив в правую часть уравнения (524.1), F/cosα вместо Fα, и разделив обе части уравнения на F, мы получим:
σF/F = рF/(Fcosα); σ = p/cosα или р = σcosα (524.3)
Соответственно найти нормальные и касательные напряжения, действующие на одну из площадок напряжений, показанную на рисунке 524.1.а) и на рисунке 524.1.б) более крупно, воспользовавшись формулами (317.2, 317.3 и 524.3) не составит большого труда:
σn = pcosα = σcosαcosα = σcos2α (524.4)
тn = psinα = σcosαsinα = (σ/2)sin2α (524.5)
Примечание: В целом все вышеизложеннное относится даже не к теории сопротивления материалов, а к геометрии и тригонометрии, поэтому вопросы, почему cosαsinα = sin2α/2 следует задавать Евклиду, Лобачевскому и прочим геометрам.
Из тех же положений геометрии следует, что максимальные касательные напряжения (чтобы не путать с максимальными нормальными, их часто называют экстремальными касательными напряжениями) будут при угле наклона площадки α = 45°, при этом касательные напряжения будут равны нормальным напряжениям (проверить это несложно, подставив значение угла а в формулы (524.4) и (524.5)).
σn(45) = σ/2 = ±тn(45) (524.6)
Если рассматривать не просто наклонное сечение, показанное на рисунке 524.1.а), а именно площадки напряжений, то при любом наклоне на всех площадках, показанных на рисунке 524.1.в) будут действовать напряжения р и соответственно, как нормальные так и касательные напряжения.
Для нижней площадки, перпендикулярной к рассмотренной выше наклонной площадке, показанной на рисунке 524.1.б) значение нормальных и касательных напряжений составит:
σn' = psinα = σsinαsinα = σsin2α (524.4.2)
тn' = - pcosα = - σsinαcosα = - тn = - (σ/2)sin2α (524.5.2)
В данном случае знак "-" означает, что проекции векторов касательных напряжений на ось у направлены в противоположные стороны.
Соответственно на взаимно параллельных площадках в виду малости рассматриваемого параллелепипеда нормальные напряжения равны по значению и направлены в противоположные стороны. Так же обстоит дело и с касательными напряжениями. При этом, как и при чистом сдвиге, векторы касательных напряжений сходятся в двух диаметрально противоположных углах. А это в свою очередь означает, что статическое равновесие системы соблюдается.
Кроме того. если сложить значения уравнений (524.4) и (524.4.2), то мы получим формулу для нахождения гипотенузы прямоугольника или уравнение радиуса окружности (отсюда и берут свое происхождение круги Мора):
σn + σn' = σcos2α + σsin2α = σ(cos2α + sin2α) = σ (524.6)
Из этого следует очень важный вывод:
Сумма нормальных напряжений на двух взаимно перпендикулярных площадках всегда равна сумме напряжений на двух главных взаимно перпендикулярных площадках и не зависит от угла наклона.
В данном случае мы рассматриваем линейное напряженное состояние и потому нормальные напряжения действуют на 2 из 6 главных площадок. Тем не менее этот вывод справедлив и для плоского напряженного состояния и в общем виде может быть записан так:
σn + σn' = σх + σу = const (524.6.2)
Т.е. линейное напряженное состояние является частным случаем плоского напряженного состояния, когда σх = σ1 = σ, σу = σ2 = 0. В данном случае индекс "1" означает, что напряжение с этим индексом является самым главным. В целом при рассмотрении любого напряженного состояния соблюдается условие: σ1 ≥ σ2 ≥ σ3. Но вернемся к линейному напряженному состоянию.
При увеличении угла наклона α значение и нормальных и касательных напряжений, действующих на площадку, рассматриваемую на рисунке 524.1.б), будет уменьшаться, а на перпендикулярные площадки - увеличиваться. При α = 90°, т.е. при рассмотрении продольного сечения стержня и нормальные и касательные напряжения на рассматриваемой площадке будут равны нулю. Формулы (524.4), (524.5) это подтверждают, σn(90) = 0. А на перпендикулярных к рассматриваемой площадках σn'(90) = ±σ, что следует из формулы (524.4.2).
Впрочем в этом нет ничего удивительного, ведь мы рассматриваем линейное напряженное состояние, т.е. повернув главные площадки напряжений на 90°, мы опять возвращаемся к главным площадкам напряжений, только при повороте на 90° на рассматриваемую площадку нормальные напряжения уже не действуют, а действуют на перпендикулярную ей площадку. Увеличивать угол наклона рассматриваемой площадки еще больше не имеет смысла, алгоритм изменения значений напряжений будет таким же.
Примечание: Если рассматривать просто некий абстрактный куб со сторонами а, то при повороте этого куба на любой угол площадь сечения его поверхностей не изменится, а значит и напряжения р, действующие на поверхности куба, должны быть равны σ, т.е. больше принятых нами. Вот только мы изначально рассматриваем некие сечения и определяем значения напряжений для этих сечений, а потом уже переходим к параллелепипеду, одна из поверхностей которого совпадает с рассматриваемым сечением.
На мой взгляд тут все достаточно просто и даже на первый взгляд не совсем понятно зачем городить этот огород из главных и наклонных площадок. Тем не менее такая необходимость есть.
Дело в том, что в реальности мы имеем дело с достаточно сложными материалами. При этом далеко не все материалы обладают изотропными свойствами, даже металлы отнести к изотропным материалам можно с большой натяжкой, а уж про древесину и тем более железобетон и говорить нечего.
Как мы знаем (во всяком случае так нас учили в школе), все материалы состоят из атомов. Атомы в свою очередь могут составлять молекулы или объединяться в кристаллические решетки (характерно для металлов). В свою очередь молекулы могут входить в состав полимеров (характерно для пластмасс) или органических соединений (характерно для древесины). Между атомами и молекулами существуют межатомные и межмолекулярные связи, характеризуемые вполне определенным расстоянием между атомами и молекулами. Под действием нагрузки материал деформируется, расстояния между атомами и молекулами изменяются и возникающие при этом напряжения направлены на то, чтобы эти расстояния восстановить. При этом значение напряжений будет зависеть от положения атомов и молекул относительно действующей нагрузки.
В общем все сложно.
Однако теория сопротивления материалов для того и разработана, чтобы максимально упростить расчет конструкций. Т.е. рассмотренный нами выше параллелепипед можно условно считать простейшей кристаллической решеткой, состоящей из 8 атомов. Но даже для металлов, действительно состоящих из кристаллических зерен (кристаллитов - кристаллов неправильной формы и разных размеров, ориентированных произвольным образом), вероятность того, что поверхности рассматриваемого параллелепипеда будут параллельны или перпендикулярны главным площадкам напряжений, близка к нулю.
А это в свою очередь означает, что даже при центральном растяжении или сжатии в материале стержня могут возникать не только нормальные, но и касательные напряжения. Это подтверждают и многочисленные результаты экспериментов. Характер деформации и виды разрушения при сжатии некоторых материалов показаны на рисунке 318.1:

Рисунок 318.5
а - для пластических материалов; б - для хрупких материалов ; в - для дерева вдоль волокон, г - для дерева поперек волокон.
Отдельно остановимся на образце из чугуна, который относится к хрупким материалам, тем не менее картина разрушения для всех хрупких материалов очень похожая:

Рисунок 524.2. Чугунный образец до и после испытаний на сжатие.
Как видим, трещины в образце имеют угол наклона примерно 45° и в итоге разрушение образца происходит в результате сдвига по одной из наклонных площадок, там где касательные напряжения максимальны.
Кроме того, на рисунке 524.2 мы видим, что чугунный образец при сжатии пытался сохранить свой объем. В итоге уменьшение высоты образца привело к увеличению диаметра, а значит и к появлению напряжений на всех главных площадках. А это означает, что даже при действии центрально приложенных сил стержень, показанный на рисунке 525.1.б), будет находиться в объемном напряженном состоянии. Определить соотношение поперечных и продольных деформаций мы можем, благодаря коэффициенту Пуассона.
Таким образом линейное напряженное состояние - не более чем допущение теории сопротивления материалов, позволяющее максимально упростить расчеты некоторых конструкций.
А спокойно пользоваться данным допущением мы можем потому, что для абсолютного большинства материалов расчетное сопротивление материала растяжению, сжатию и т.п. определяется опытным путем. Т.е. данные расчетные сопротивления уже учитывают объемное напряженное состояние материала при центральном растяжении или сжатии.
А теперь рассмотрим плоское напряженное состояние материала более подробно. | 
