Так как сопротивление металла сдвигу или срезу при действии касательных напряжений значительно меньше сопротивления растяжению, сжатию или изгибу при действии нормальных напряжений, то расчет угловых сварных швов (расчет на условный срез) сводится к определению касательных напряжений, которые должны быть меньше расчетного сопротивления.
Предполагается, что разрушение углового сварного шва может произойти в двух плоскостях: по металлу шва и по границе сплавления, поэтому расчет угловых швов производится для этих двух сечений:

Рисунок 529.3. Расчетные сечения угловых швов
А теперь рассмотрим возможные напряженные состояния элементов, соединяемых угловыми швами, более подробно.
Расчет угловых сварных швов производится по следующим формулам:
1. Расчет угловых швов при центральном растяжении (рисунок 529.2.д)) или сжатии (действии силы N)

Рисунок 529.2. Основные виды сварных соединений с угловыми швами.
И лобовые и фланговые швы рассчитываются на условный срез
1.1. по металлу шва (сечение 1 на рисунке 529.3):
тwf = N/(βfkflw) ≤ Rwfγc (531.1)
где N - значение продольной растягивающей (или сжимающей) силы, приложенной по оси, совпадающей с центром тяжести сечения (без эксцентриситета). Может измеряться в кгс, тс, Н, кН;
βf - безразмерный коэффициент, определяемый по следующей таблице:
Таблица 529.2. (согласно СНиП II-23-81* "Стальные конструкции")

Примечание: почему при расчетах я рекомендую пользовать именно этой таблицей, а не таблицей из актуализированной редакции указанного СНиПа, достаточно подробно объясняется в статье, посвященной рассмотрению основных видов сварных швов.
kf - катет углового шва. Принимается по конструктивным требованиям или согласно расчету. Измеряется в мм или см.
lw - суммарная длина угловых швов с учетом непровара в начале и в конце шва. Например, если рассчитывается один угловой шов длиной l, то его расчетная длина составит:
lw = l - 2t (529.1.1)
где t - толщина наименьшей из свариваемых деталей.
В целом произведение βfkflw - это и есть площадь рассматриваемого сечения.
Rwf - расчетное сопротивление срезу по металлу шва. Определяется по следующей таблице:
Таблица 530.2. Расчетные сопротивления сварных соединений (согласно СП 16.13330.2011 "Стальные конструкции")

Примечания:
1. Значения коэффициентов надежности по металлу шва γwm следует принимать:
γwm = 1,25 - при Rwun ≤ 490 Н/мм2 (4900 кг/см2);
γwm = 1,35 - при Rwun ≥ 590 Н/мм2 (5900 кг/см2)
Значения Rwun и Rf определяются по следующей таблице:
Таблица 531.1. (согласно СП 16.13330.2011 "Стальные конструкции")

Примечание:
В ныне неактуальном СНиП II-23-81* и старых справочниках, таблица вида 530.2 сопровождалась следующими примечаниями:
1. Для угловых швов, выполняемых ручной сваркой, значения Rwun принимают равными значениям временного сопротивления разрыву металла шва (σв) согласно ГОСТ 9467-75*.
Приводить здесь таблицу из ГОСТа, по которой можно определить временное сопротивление разрыву шва, я не буду. Просто скажу, что в маркировке электродов это значение уже указано в кгс/мм2. Например:
- для электродов Э38 Rwun = σв = 38 кгс/мм2 (3800 кгс/см2)
- для электродов Э42А Rwun = σв = 42 кгс/мм2 (4200 кгс/см2) и так далее вплоть до Э150 (сейчас такие марки электродов даже и не рассматриваются).
На мой взгляд это учень удобно, тем не менее сейчас все принято выражать в единицах системы СИ, что и отображено в таблице 531.1.
γс - коэффициент условий работы элементов конструкций и соединений, принимаемый по следующей таблице:
Таблица 530.3. Коэффициенты условий работы элементов и соединений стальных конструкций (согласно СП 16.13330.2011 "Стальные конструкции")

1.2. По металлу границы сплавления (сечение 2 на рисунке 529.3):
тwz = N/(βzkflw) ≤ Rwzγc (531.2)
где βz - безразмерный коэффициент, определяемый по таблице 529.2.
Rwz - расчетное сопротивление металла на границе сплавления, определяемое по таблице 530.2, где Run - нормативное сопротивление проката, определяемое по следующей таблице:
Таблица 171.8. (согласно ГОСТ 27772-88 для стальных конструкций зданий и сооружений)
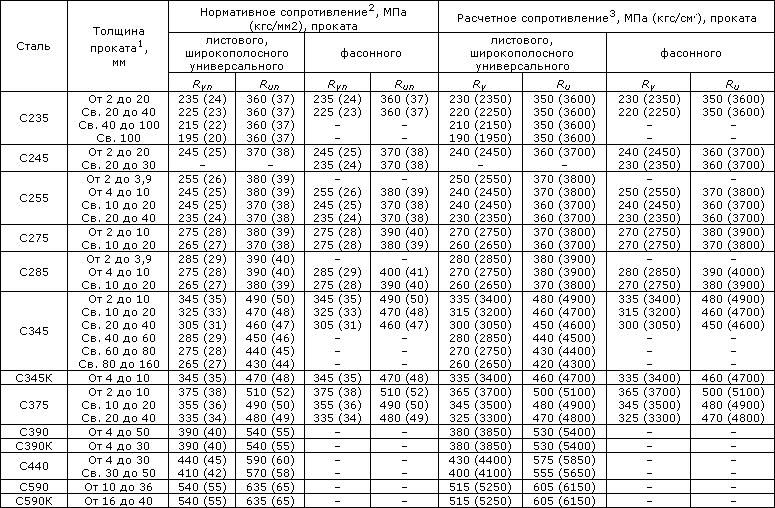
Примечание: заменяемые марки стали приводятся отдельно.
Тут добавлю, что при центральном растяжении или сжатии элемента из свариваемых деталей во фланговых швах на обеих катетах шва будут действовать касательные напряжения. В лобовых швах на одном из катетов будут действовать растягивающие или сжимающие нормальные напряжения, имеющие такое же значение, как и касательные напряжения на втором катете.
Я это все к тому, что иногда в справочниках напряжения, определяемые для других видов напряженно-деформированного состояния обозначаются как нормальные, т.е. литерой "σ". Формально тут большой ошибки нет и делается это больше для того, чтобы различать напряжения, возникающие при действии изгибающего момента и других возможных воздействий. Но все равно нельзя забывать, что расчет производится именно на условный срез, т.е. на действие касательных напряжений, имеющих, впрочем, такое же значение, как нормальные на втором катете. А вот направления действия касательных напряжений действительно могут быть разными, что мы вскоре и увидим.
2. Расчет сварных соединений с угловыми швами при действии изгибающего момента М в плоскости, перпендикулярной плоскости расположения швов
Т.е. в данном случае имеется в виду, что через рассматриваемые швы можно провести одну плоскость и эта плоскость будет перпендикулярна плоскости действия момента. К положению плоскости, в которой может произойти разрушение шва, данная формулировка никакого отношения не имеет.
Как правило такая ситуация возникает при расчете сварного соединения втавр двухсторонними швами (рисунок 529.2.г)) или односторонними швами (рисунок 529.3). При этом угловые швы рассчитываются на условный срез
2.1. по металлу шва (сечение 1 на рисунке 529.3):
М/Wf ≤ Rwfγc (531.3)
2.2. по металлу границы сплавления (сечение 2 на рисунке 529.3):
М/Wz ≤ Rwzγc (531.4)
где М - значение изгибающего момента, определяемое по эпюре "М".
Wf и Wz - моменты сопротивления расчетных сечений сварного соединения по металлу шва и по границе сплавления с металлом соответственно.
Например при соединении втавр двухсторонними швами моменты сопротивления составят:
Wf = 2(βfkflw2/6) = βfkflw2/3 (531.3.1)
Wz = 2(βzkflw2/6) = βzkflw2/3 (531.4.1)
Как правило, разделив момент М на момент сопротивления W, мы определяем нормальные напряжения, поэтому в некоторых старых учебниках и справочниках (например: А.П.Мандриков, Примеры расчета металлических конструкций, М.-1991) формулы (531.3) и (531.4) имеют другую форму записи, примерно такую:
σwf = М/Wf ≤ Rwfγc (531.3.2)
σwz = М/Wz ≤ Rwzγc (531.4.2)
Но сути это не меняет.
Примечания:
1. В СНиП II-23-81* и старых справочниках значение расчетного сопротивления Rwf и Rwz при всех возможных расчетных случаях дополнительно умножалось на коэффициенты условий работы шва γwf или γwz соответственно.
Значение этих коэффициентов принималось равным 1 во всех случаях, кроме конструкций, возводимых в климатических районах I1 (согласно ГОСТ 16350-80: очень холодный, среднемесячная температура воздуха в январе от -50 до -30), I2 (холодный, температура от -30 до -15), II2 (арктический восточный, температура от -28 до -18) и II3 (арктический западный, температура от -30 до -2), для которых γwf = 0.8 при Rwun = 410 МПа и γwz = 0.85 для всех сталей.
На мой взгляд данное ограничение значения расчетного сопротивления вводилось с целью уменьшения риска хрупкого разрушения сварного соединения при низких температурах. Сейчас оно не действует, но думаю, знать о нем надо.
2. Вообще-то это примечание следовало сделать при рассмотрении первого раздела, но он и так получился перенасыщенным информацией, поэтому оставлю это примечание здесь.
3. Расчет угловых швов при действии изгибающего момента М в плоскости, перпендикулярной плоскости швов и действии продольной силы N
Подобная ситуация часто встречается при расчете разного рода опорных площадок, поэтому я выделил ее в отдельный раздел, хотя в СП 16.13330.2011 такой вариант загружения отдельно не рассматривается.
Тем не менее, при загружении опорной площадки некоторой силой, приложенной с эксцентриситетом, возникает следующая ситуация, которую я решил проиллюстрировать картинкой из все того же А.П.Мандрикова:

Рисунок 531.1.
В этом случае угловые швы рассчитываются на условный срез
3.1. по металлу шва:
(тwf2 + σwf2)1/2 ≤ Rwfγc (531.5)
3.2. по металлу границы сплавления:
(тwz2 + σwz2)1/2 ≤ Rwzγc (531.6)
где значение касательных напряжений определяется в зависимости от рассматриваемого сечения по формулам (531.1) и (531.2), а значение условно нормальных напряжений - по формулам (531.3.2) и (531.4.2) соответственно.
Примечание:
Конечно же согласно требований ныне действующих нормативных документов более правильно вести речь только о касательных напряжениях относительно осей х и у. Т.е. тwf = тy, σwf = тх и так далее, но как уже говорилось, на окончательные результаты расчета это ни как не влияет, при этом старый подход выглядит более наглядным.
4. Расчет угловых швов при действии изгибающего момента М в плоскости сварных швов
Подобная ситуация часто встречается при расчете стыковых соединений с накладками, т.е. при одновременном использовании и лобовых и фланговых швов (см. рисунок 529.2.в)), а также при соединении внахлест лобовыми или фланговыми швами (см. рисунок 529.2.а) и б)). Это означает, что как и в предыдущем случае касательные напряжения действуют как вдоль оси х, так и вдоль оси у. Соответственно задача сводится к определению равнодействующей этих двух напряжений. Расчет в этом случае выполняется по следующим формулам:
4.1. по металлу шва:
тМ = М(х2 + у2)1/2/(Ifx + Ify) ≤ Rwfγc (531.7)
4.2. по металлу границы сплавления:
тМ = M(x2 + y2)1/2/(Izx + Izy) ≤ Rwzγc (531.8)
где х и у - координаты рассматриваемой точки сварного соединения относительно главных осей х-х и у-у. Как правило рассматриваемая точка максимально удалена от центра тяжести О расчетного сечения.
Ifx, Ify, Izx, Izy - моменты инерции рассматриваемых сечений швов относительно главных осей.
Так как рассчитываемые швы находятся в одной плоскости с действующим моментом, то для определения указанных моментов инерции необходимо кроме катета, длины шва и соответствующих коэффициентов также знать расстояние между швами, чего не требовалось при рассмотрении швов, находящихся в плоскости, перпендикулярной плоскости действия момента.
В нормативных документах вопросу определения моментов инерции для угловых сварных швов внимания не уделяется, но на мой взгляд это достаточно сложный вопрос и вообще его рассмотрению следует посвятить отдельную статью, а пока ограничимся следующим примером:
При соединении внахлест только лобовыми швами и при расстоянии между центрами тяжести лобовых швов, равном l (центры тяжести и расстояние l на рисунке 529.2.а) не показаны), значения моментов инерции для сечения металла шва составят:
Ifx = 2βfkflw3/12 = βfkflw3/6 (531.9)
Ifу = 2βfkf3lw/12 + 2(l/2)2βfkflw = βfkf3lw/6 + l2βfkflw/2 (531.10)
5. Расчет угловых швов при действии момента М, продольной N и поперечной V сил в плоскости сварных швов
Это наиболее общий случай напряженно-деформированного состояния, проиллюстрированный в СП 16.13330.2011 следующим образом:

Рисунок 531.2. Расчетная схема сварного соединения с угловыми швами в общем случае загружения.
Расчет в этом случае выполняется по следующим формулам:
5.1. по металлу шва:
тf ≤ Rwfγc (531.11)
5.2. по металлу границы сплавления:
тz ≤ Rwzγc (531.12)
где тf и тz - касательные напряжения в рассматриваемой точке расчетного сечения сварного соединения по металлу шва и по металлу границы сплавления, определяемые по формуле:
т = ((тN + тМх)2 + (тV + тМу)2)1/2 (531.13)
где тN и тV - касательные напряжения, определяемые по формулам (531.1) и (531.2), а тМх и тМу - горизонтальная и вертикальная составляющие касательных напряжений при действии момента, определяемые по следующим формулам:
тМх = Мх/Iy (531.14)
тМу = Му/Iх (531.15)
Но и это еще не все. При проектировании строительных конструкций необходимо также соблюдать конструктивные требования, предъявляемые к сварным соединениям. | 
