1. Все основные величины, используемые при расчете строительных конструкций, в частности балок постоянного сечения, связаны между собой следующими дифференциальными зависимостями:
1.1. Поперечная сила Q в рассматриваемом сечении балки - это производная от изгибающего момента M в этом же сечении. Координата рассматриваемого сечения как правило определяется по оси х, тогда:
Qx = (Mx)' = dMx/dx (537.1)
1.2. Распределенная нагрузка qx - это производная от поперечной силы Qx или вторая производная от изгибающего момента Мх:
qx = (Qx)' = (Mx)" = dQx/dx = d2Mx/dx2 (537.2)
1.3. Тангенс угла поворота θх - это производная функции y, описываемой уравнением прогиба:
tgθх = (y)' = dy/dx (537.3)
1.4. При этом прогиб f рассматривается, как координата у в рассматриваемой точке или как кривизна нейтральной оси балки в данной точке:
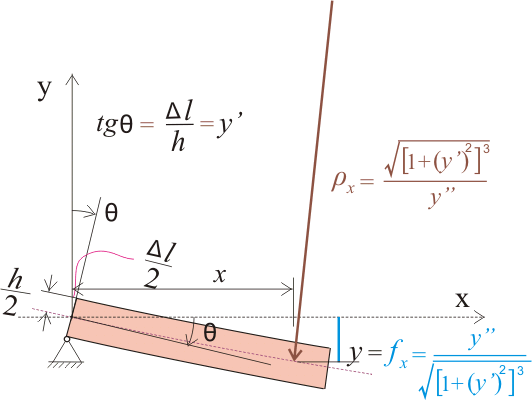
Рисунок 537.1. Радиус кривизны и тангенс угла поворота для однопролетной балки на шарнирных опорах при действии симметричной нагрузки.
fх = kx = y"/((1 + (dy/dx)2)3/2 (537.4)
так как при деформации в пределах упругости кривизна нейтральной оси в рассматриваемой точке составляет:
kх = 1/рх (542.1)
При малых значениях угла поворота, а как правило эти углы при деформациях балок не превышают 0.3-0.6°, значением квадрата первой производной на значение прогиба можно пренебречь. Например tg0.6° = 0.01, а (tg0.6°)2 = 0.00011. Это позволяет определять прогиб по упрощенной формуле:
fх = y" = d2y/dx2 (537.4.2)
Примечание
Изложенный выше подход, когда кривизна балки в некоторой точке рассматривается как прогиб или координата у в этой точке на эпюре прогибов, т.е. kх = yх = fх, часто встречается в учебниках и справочниках по теории сопротивления материалов, а также в нормативных документах, например в СП 52-101-2003, СНиП 2.03.01-84 и других.
Между тем такой подход кажется мне не правильным по двум причинам:
1. Кривизна - это некоторая величина, обратная длине, т.е. измеряемая в 1/м или 1/см. Между тем прогиб измеряется в м или см. Т.е. на лицо явное логическое несоответствие.
2. При больших значениях угла поворота k ≠ f и в этом достаточно легко можно убедиться.
Например, если у нас нейтральная линия балки соответствует дуге m с радиусом 3, как показано на рисунке 537.2 (что конечно же маловероятно, но теоретически возможно):

Рисунок 537.2. Дуга, соответствующая положению нейтральной линии балки.
То в этом случае, даже без сложных вычислений понятно, что кривизна дуги составляет k = 1/3 = 0.333 (на рисунке 537.2 эта условная величина показана зеленой линией). Между тем прогиб в точке В - это ΔR = 0.878 = у = f (на рисунке 537.2 эта вполне конкретная величина показана красной линией).
Мы конечно же можем в данном случае определить кривизну дуги и более сложным путем, исходя из того, что tg45° = 1 - первая производная рассматриваемой функции, у = 0.878 - вторая производная рассматриваемой функции. Тогда, если мы разделим 0.878 на (1 + 12)3/2, то получим 0.31, что примерно соответствует значению кривизны дуги, определенному более простым способом. Вот только кривизна дуги по-прежнему ни как не равна прогибу в рассматриваемой точке, тем более при больших значениях первой производной.
С чем именно связан столь странный подход к прогибу, как кривизне, в учебниках, справочниках и нормативных документах, я судить не берусь. Возможно таким способом устраняется другое логическое несоответствие. Ведь когда мы строим эпюры - графики функций, то по оси х откладываем полученные значения по всей длине балки l, принимая ось х совпадающей с нейтральной линией балки. Но в действительности положение нейтральной линии балки описывается кривой графика прогиба - эпюрой прогиба (например дугой m на рисунке 537.2). Очевидно, что чем больше прогиб, тем больше разница между l и длиной кривой на графике прогиба. Эту разницу можно назвать условным уменьшением длины балки. Таким образом можно предположить, что при достаточно больших значениях прогиба условное уменьшение длины балки учитывается использованием соответствующих формул, однако это не более, чем мое предположение.
С одной стороны об этом можно было бы и не упоминать, тем более, что в абсолютном большинстве случаев при расчетах тангенс угла наклона - действительно достаточно малая величина и можно использовать упрощенную формулу (537.4.2). С другой стороны знать об этой странности все-таки нужно, потому что, как я уже говорил, именно такой подход используется в учебниках, справочниках и нормативных документах.
Продолжим.
Угол поворота поперечного сечения θ и прогиб f - вертикальное смещение нейтральной оси балки зависят от жесткости балки. Чем больше жесткость, тем меньше угол поворота и прогиб. В свою очередь жесткость балки зависит от модуля упругости материала балки Е и от момента инерции поперечного сечения I. Поэтому зависимость между моментом, углом поворота и прогиба выражается с учетом допустимого упрощения определения прогиба следующим образом:
1.5. Изгибающий момент Мх - это с учетом жесткости производная тангенса угла поворота θх или вторая производная функции у, описываемой уравнением прогиба:
Mx/EI = (tgθx)' = (у)"= dtgθx/dx = d2fx/dx2 (537.5)
Кроме того, так как углы поворота поперечных сечений достаточно малы, то предполагается, что:
tgθх = θх = dfx/dx (537.3.2)
И хотя это не так, в чем мы убедились, определив тангенс угла 0.6°, тем не менее такое допущение, а также упрощенное определение прогиба позволяют значительно упростить запись уравнения зависимости между всеми указанными величинами:
qx = (Qx)' = (Mx)" = (θx)'''/EI = (fx)""/EI (537.6)
2. Как правило при расчете строительных конструкций решается обратная задача. Т.е. известна действующая нагрузка на балку, выражаясь языком математики, есть уравнение, описывающее характер изменения нагрузки - уравнение функции q, в общем виде имеющее следующую запись у = f(x), а в итоге нужно определить прогиб. В данном случае обозначим прогиб w, чтобы не путать с выражением функции (ничего не поделаешь, для обозначения всевозможных величин литер латинского и греческого алфавита уже давно не хватает) . Соответственно:
Qx = ∫f(x)dx + C = ∫qxdx + Q0 (537.7)
В данном случае постоянная интегрирования C - это и есть начальный параметр Q0. Если начало координат совпадает с одной из опор балки, то значение этого параметра соответствует значению опорной реакции (значению поперечных сил в поперечном сечении на опоре). Дальше постоянные интегрирования будут обозначаться произвольными литерами, а не в алфавитном порядке, как это иногда делается.
Mx = ∫dx∫f(x)dx + Сx + D = ∫Qxdx + M0 + Q0x (537.8)
EIθx =∫dx∫dx∫f(x)dx + Cx2/2 + Dx + В = ∫Mxdx + θ0EI + M0x + Qx2/2 (537.9)
EIwx = ∫dx∫dx∫dx∫f(x)dx + Сx3/6 + Dx2/2 + Bx + A =
= ∫θxdx + w0EI + θ0xEI + M0x2/2 + Q0x3/6 (539.10)
Соответственно, если начало координат совпадает с опорой балки, то М0 - это значение момента в поперечном сечении на данной опоре, θ0 - угол поворота поперечного сечения на данной опоре (см. рис.537.1), w0 - прогиб на данной опоре.
Как правило начало координат выбирается так, чтобы хотя бы один из начальных параметров был известной величиной, как правило равной нулю. Если начало координат совпадает с шарнирной опорой, то такой известной величиной будет прогиб. Если начало координат совпадает с началом консольной балки, то такими известными величинами, равными нулю, будут изгибающий момент и поперечная сила. Если начало координат - это жесткое защемление балки, то начальный прогиб и угол поворота будут равны нулю.
А если хотя бы один начальный параметр известен, то решая уравнения (537.7)-(537.10), мы можем определить не только остальные начальные параметры, но и все остальные требуемые значения, например, прогиб или угол поворота.
Таким образом уравнения (537.7)-(537.10) - это уравнения начальных параметров. А определение искомых неизвестных величин путем решения этих уравнений - это и есть метод начальных параметров. | 
