В общем случае определение дифференциального уравнения может выглядеть так:
Дифференциальным уравнением называется равенство между функцией и ее производной или дифференциалом.
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного аргумента. Например:
у' = f(x) (539.1)
Напомню, функциональное уравнение может иметь следующий вид:
у = f(x) (538.1)
Дифференциальное уравнение называется уравнением в частных производных, если искомая функция зависит от нескольких аргументов. Например:
у' = f(x1,x2) или у' = f(x,u) (539.2)
где х1, х2 или х, u - возможные обозначения для различных аргументов функции.
Порядком дифференциального уравнения считается порядок наивысшей производной, входящей в уравнение. Например уравнение (539.1) является уравнением первого порядка. Уравнение второго порядка может иметь вид:
y" = f(x) (539.3)
Решением дифференциального уравнения является функция, подставление которой вместо неизвестной функции обращает уравнение в тождество. Другими словами уравнение становится равенством.
А теперь эти общие математические понятия (кстати тут приведены далеко не все основные понятия) попробуем описать простым человеческим языком, но начать придется издалека.
Производная функции
Мы живем в несовершенном, постоянно изменяющемся мире. Все течет, все изменяется, как подметил еще Гераклит. Однако в древности были и другие мыслители, которые в отличие от Гераклита пытались этот мир как-то понять и оценить. Так далеко в историю мы заглядывать не будем, хотя предпосылки к дифференциальному исчислению следует искать именно там, а ограничимся простыми и наглядными примерами:
Пример 1
Мы вышли из пункта А в пункт Б и находились в пути 4 часа, каждый час мы проходили по 2 километра. Вопрос: какое расстояние между пунктами А и Б?
Вообще это задачка для 3-4 класса начальной школы и решить ее вроде бы не сложно (потому я ее и выбрал): достаточно сложить все расстояния, пройденные за каждый час, а так как эти расстояния одинаковые, то можно еще больше упростить задачу, умножив на 4 расстояние, пройденное за один промежуток времени. Таким образом расстояние между пунктами А и Б составляет:
2 км · 4 = 8 км (539.4)
А между тем условия задачи можно рассматривать и по другому, т.е. как зависимость пройденного расстояния от времени. В этом случае у нас время -независимая переменная t или аргумент функции, а пройденное расстояние - значение функции в тот или иной момент времени или переменная s. Тогда условия задачи соответствуют следующему функциональному уравнению:
s = f(t) = 2t (539.5)
а также графику этой функции:
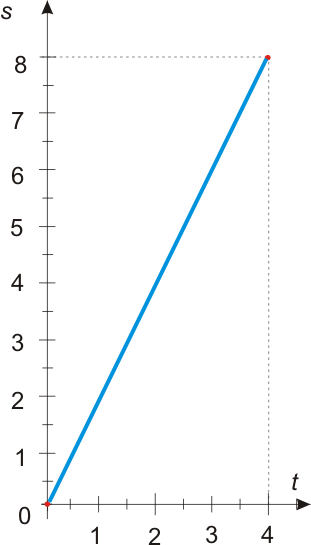
Рисунок 539.1. График функции f(t) = 2t.
Так если по оси t откладывать промежутки времени Δt (ч), которое мы были в пути, а по оси s - преодоленное за эти промежутки времени расстояние Δs (км), то график указанной функции будет иметь такой вид, как показано на рисунке 539.1. В общем случае используются более привычные оси х и у, соответственно рассматриваются функции вида y = f(x), но сути дела это никак не меняет.
Решая уравнение (539.5) мы можем определить не только общее расстояние, преодоленное за 4 часа пути, но и в любой интересующий нас момент времени. Например, нас интересует, какое расстояние мы прошли за 1.5 часа. Согласно уравнению (539.5) это расстояние составит 2·1.5 = 3 километра.
А если нас интересует не расстояние, преодоленное к тому или иному моменту времени, а скорость движения? Можем ли мы определить эту скорость на основе имеющихся данных?
Оказывается можем, потому что скорость - это тоже функция, которая в свою очередь также зависит от времени.
Так как каждый час мы преодолевали по 2 км, то отсюда можно сделать вывод, что скорость нашего движения была постоянной, тогда по давно известному нам уравнению, описывающему движение с постоянной скоростью:
v = s/t = 8/4 = 2 км/ч (539.6)
В данном случае, так как скорость постоянная, не имеет значения, на каком временном промежутке мы эту скорость определяем. Тем не менее рассмотрим данную ситуацию с точки зрения математики.
Временные промежутки, когда засекалось пройденное расстояние, мы обозначим как Δt = 1, соответственно t = ΣΔt = 1 + 1 + 1 + 1 = 4. Расстояния, пройденные за эти промежутки времени обозначим как Δs = 2. На графике функции это будет выглядеть так:

Рисунок 539.2
С точки зрения математики временные промежутки Δt - это приращение аргумента функции:
Δt = t - t0 (539.7)
Соответственно расстояния, пройденные за рассматриваемый промежуток времени - это приращение функции:
Δs = Δf(t) = f(t) - f(t0) (539.8)
А так как использовать греческую литеру Δ не всегда удобно (в частности мне для этого приходится заходить в отдельный редактор текста, а наборщикам в типографиях вставить эту литеру было еще сложнее), то часто приращение значения искомой функции и приращение аргумента функции обозначают как ds и dt.
Тогда формулу определения скорости можно записать так:
v = ds/dt (539.9)
Таким образом мы с одной стороны вроде бы просто разделили расстояние на время - задача для 3-4 класса, а с другой стороны мы определили производную функции s = f(t), соответствующим образом ее продифференцировав, а это уже задача курса алгебры, а то и высшей математики.
Возможно и не стоило это так подробно расписывать, но на мой взгляд это очень важно, чтобы показать, что в дифференциальном исчислении нет ничего трудного, если рассматривать его на соответствующих примерах.
Итак скорость v является производной функции s = f(t) = 2t. Дифференциальное уравнение в этом случае будет выглядеть так:
v = s' = f'(t) (539.10.1)
v = (2t)' = 2 (539.10.2)
Но и это еще не все, на основании имеющихся данных: времени в пути и расстояний, преодоленных за 1 час, мы можем определить ускорение нашего движения.
Так как скорость нашего движения оставалась постоянной, соответственно dv = 0, то само собой и ускорения никакого не было, ни положительного ни отрицательного. Другими словами ускорение нашего движения составляло а = 0 км/ч2.
На языке математики это будет выглядеть так:
а = v' = dv/dt = s" = d2s/dt2 (539.11.1)
a = 0/1 = (2t)" = (2)' = 0 (539.11.2)
Т.е. в данном случае для определения ускорения нужно определить первую производную функции скорости (уравнения, выражающего зависимость скорости от времени) или вторую производную функции расстояния (уравнения, выражающего зависимость пройденного расстояния от времени).
На основании вышеизложенного мы можем дать следующее предварительное определение производной:
Производная - это скорость изменения функции
В рассмотренном выше примере скорость движения - это скорость изменения функции расстояния, а ускорение - это скорость изменения функции скорости. Если бы мы все 4 часа сидели на месте, то и расстояние, пройденное нами, было бы равно нулю, и скорость и ускорение, но даже для такого случая можно записать соответствующие дифференциальные уравнения:
s = f(t) = 0
v = s' = 0
a = v' = s" = 0
Однако в жизни гораздо чаще встречаются функции, даже третьи производные которых не равны нулю.
Рассмотрим другой пример все с тем же движением, на этот раз чуть более сложный.
Пример 2
По ровной наклонной поверхности скатывается шар. Начальная скорость движения равна vo = 0. Определить пройденное шаром за 4 секунды расстояние, скорость после 1, 2, 3 и 4 секунд движения и постоянное ускорение движения, если за первую секунду шар преодолел расстояние 3 м, за вторую - 9 м, за третью - 15 м, за четвертую - 21 м.
С определением пройденного расстояния по прежнему проблем нет: достаточно сложить расстояния, которые преодолел шар за каждую секунду s = ΣΔs = 3 + 9 + 15 + 21 = 48 метров. А вот скорость и ускорение в данном случае определить не так просто. Тем не менее попробуем.
Если воспользоваться полученными раннее знаниями, то вроде бы в первый промежуток времени скорость должна быть равна:
v1 = ds1/dt1 = 3/1 = 3 м/с (539.12)
Вот только в данном случае у нас скорость - изменяющаяся величина, зависящая от времени, поэтому результат полученный при решении уравнения (539.12) можно рассматривать лишь как среднюю скорость движения на первом участке. Тогда более правильно уравнение скорости на первом участке записать так:
v1ср = ds1/dt1 = 3/1 = 3 м/с (539.12.2)
Подобным образом мы достаточно легко можем определить среднюю скорость на всех участках пути, и она составит v2ср = 9 м/с, v3ср = 15 м/с, v4ср = 21 м/с, но в данном случае нас интересует не среднее значение функции скорости на рассматриваемом участке, а значение функции скорости во вполне определенной точке, т.е. после 1, 2, 3 и 4 секунд движения. Как это сделать?
По условиям задачи ускорение - производная от скорости - является постоянной величиной, т.е. скорость изменения скорости будет постоянной. В этом случае значение средней скорости является средним арифметическим от начальной и конечной скорости на рассматриваемом участке:
v1ср = (vo + v1)/2 = 3 м/с (539.13.1)
тогда при vo = 0
v1 = 3·2 = 6 м/с (539.13.2)
Соответствующим образом мы можем определить значения скорости и в остальных точках, например (6 + v2)/2 = 9, v2 = 9·2 - 6 = 12 м/с; (12 + v3)/2 = 15, v3 = 15·2 - 12 = 18 и так далее, а теперь переведем полученные данные на язык высшей математики. Мы видим, что v1 = 6·1, v2 = 6·2 = 12, v3 = 6·3 = 18, т.е. значение скорости явно зависит от времени, соответственно уравнение скорости мы можем записать следующим образом:
v = s' = 6t (539.14)
Соответственно ускорение движения шара составит:
a = v' = (6t)' = 6 м/с2 (539.15)
Между тем, если бы нам были заданы меньшие значения временных промежутков и соответственно меньшие значения пройденных расстояний за эти промежутки времени, например при dt1 = 1 секунда, ds1 = 3 м, dt2 = 0.1 секунды и ds2 = 0.63 м, то средняя скорость на рассматриваемом втором участке составила бы v2ср = ds/dt = 0.63/0.1 = 6.3 м/с, а скорость в в точке t2: v2сp = (6 + v2)/2 = 6.3, v2 = 12.6 - 6 = 6.6 м/с. Т.е. закономерность изменения значения скорости никуда не девается, тем не менее, чем меньше рассматриваемый временной промежуток dt, тем меньше разница между значением средней скорости изменения функции и скоростью изменения функции в рассматриваемой точке. Из этого можно сделать еще один очень важный вывод:
Скорость изменения функции может быть разная. Чем меньше приращение аргумента функции dt, тем ближе значение среднего изменения скорости к изменению скорости функции в рассматриваемой точке.
На основании этого можно сформулировать более полное определение производной функции:
Производная функции в точке - это скорость изменения функции в рассматриваемой точке при стремлении приращения аргумента функции к нулю (Δt → 0)
Поэтому иногда производную называют мгновенной скоростью изменения функции. В нашем случае уравнение производной будет выглядеть так:
 (539.16) (539.16)
На данном этапе вид формулы (539.16) нас уже не пугает (во всяком случае мне так кажется). Совсем другое дело, когда подобная формула приводится в начале темы, посвященной рассмотрению производных функции.
Дифференциал (первообразная) функции
С задачей определения скорости и ускорения в примере 2 мы вроде бы справились и даже составили соответствующие уравнения (539.14) и (539.15). Но иногда требуется решить и обратную задачу - например определить исходное уравнение, описывающее зависимость перемещения от времени.
Если скорость является производной функции расстояния v = s', то расстояние при этом является первообразной (дифференциалом) функции скорости s = ∫v. Процесс нахождения первообразной функции называется интегрированием. Так, чтобы получить уравнение зависимости пройденного расстояния от времени, нам нужно проинтегрировать уравнение скорости. При этом уравнение расстояния более правильно записывать так
s = ∫vdt (539.17)
В общем случае интегрирование может быть более сложной задачей, чем дифференцирование, потому что функции бывают не только степенными, как в данном примере, но и тригонометрическими, обратными тригонометрическими и т.п., но пока нас интересует, как проинтегрировать простую степенную функцию вида f(t) = 6t.
Вообще-то мы могли сразу построить график, отражающий зависимость пройденного расстояния от времени по данным примера 2, тем не менее сделаем это сейчас, а заодно построим график для уравнений скорости и ускорения и расположим их в такой последовательности:

Рисунок 539.3. Графики степенных функции а) а= 6, б) v = at, в) s = at2/2.
Как видим, график, отражающий зависимость ускорения от времени, у нас самый простой. Ускорение постоянное, а = 6 м/с2 и от времени никак не зависит. Тем не менее, зная ускорение, мы можем определить скорость движения в любой точке времени. Так из уравнений (539.14) и (539.15) следует, что:
v = 6t = at (539.14.2)
Соответственно решая это уравнение, мы можем определить скорость в любой момент времени.
Но если рассматривать это действие с точки зрения геометрии, то мы, умножая ускорение на время, определяем площадь прямоугольника со сторонами а = 6 и t. При t = 4 площадь прямоугольника составит 6·4 = 24, точнее 24 м/с так как мы все-таки определяем скорость.
Если мы построим график, отражающий зависимость изменения скорости от времени, то увидим, что на этом графике значения скорости в той или иной момент времени соответствуют площадям прямоугольника со сторонами а = 6 и t.
Получается, что если определить площадь треугольника со сторонами v и t, то это и будет расстояние, преодоленное к тому или иному промежутку времени:
s = vt/2 = at2/2 = 6t2/2 = 3t2 (539.18)
Уравнение (539.18) можно записать как дифференциальное:
s = ∫6tdt = 3t2 (539.18.2)
Если график, показанный на рисунке 539.3.в) также является графиком для производной некоторой функции, то для определения первообразной этой функции нам также следовало бы найти площадь фигуры, ограниченной квадратной параболой.
Сделать это в принципе не сложно, так как площадь фигуры, очерченной квадратной параболой таким образом, как показано на рисунке 539.3.в) в 3 раза меньше площади прямоугольника со сторонами s и t, соответственно S = st/3 = 3t2t/3 = t3 и эту процедуру можно повторять до бесконечности.
Почему площадь фигуры, ограниченной квадратной параболой именно в 3 раза меньше, чем площадь прямоугольника, а площадь фигуры ограниченной кубической параболой в 4 раза меньше площади прямоугольника, я здесь объяснять не буду, тем не менее такая закономерность существует и в математическом выражении выглядит так:
∫aхndx = axn+1/n + C (539.19)
В данном случае С - это некоторая постоянная величина. Как мы выяснили, при дифференцировании постоянные величины обращаются в нуль, как пример - уравнение (539.11.2), соответственно решая обратную задачу, т.е. интегрируя функцию, мы допускаем, что некая постоянная величина в первообразной функции была.
Например в общем случае уравнение скорости (539.14.2) должно выглядеть так:
v = vo + at (539.14.3)
где vo - это и есть некая постоянная величина. В нашем случае по условиям задачи vo = 0, поэтому мы использовали сокращенную форму записи.
Определенный интеграл
В общем случае график функции может выглядеть как угодно, например так:

Рисунок 539.4
В этом случае сразу определить площадь фигуры, ограниченной графиком функции, не получится. Но мы можем разбить эту фигуру на участки шириной Δх и определить среднее значение у для каждого участка. Теперь определить площади трех прямоугольников большого труда не составит, вот только суммарная площадь прямоугольников не будет равна площади фигуры, ограниченной графиком функции:
S ≈ ∑yiΔx (539.20)
Но чем больше будет у нас прямоугольников с шириной Δх, т.е, чем меньше будет значение Δх, тем точнее будет значение у, а значит и суммарная площадь прямоугольников будет ближе к площади фигуры, ограниченной графиком функции.
При интегрировании, как и при дифференцировании для получения более точного результата приращение аргумента функции должно стремиться к нулю (maxΔx → 0).
Из этого можно сделать следующий вывод:
Если существует предел суммы, определяемой по формуле (539.20) вне зависимости от количества прямоугольников и при стремлении ширины прямоугольников к нулю, то такой предел называется определенным интегралом, а суммы, определяемые по формуле (539.20) - интегральными суммами.
Так как на рисунке 539.4 показан график непрерывной функции, то такая функция является интегрируемой и для определения дифференциала функции используется определенный интеграл. При этом 0 и 3 - это пределы интегрирования. | 
