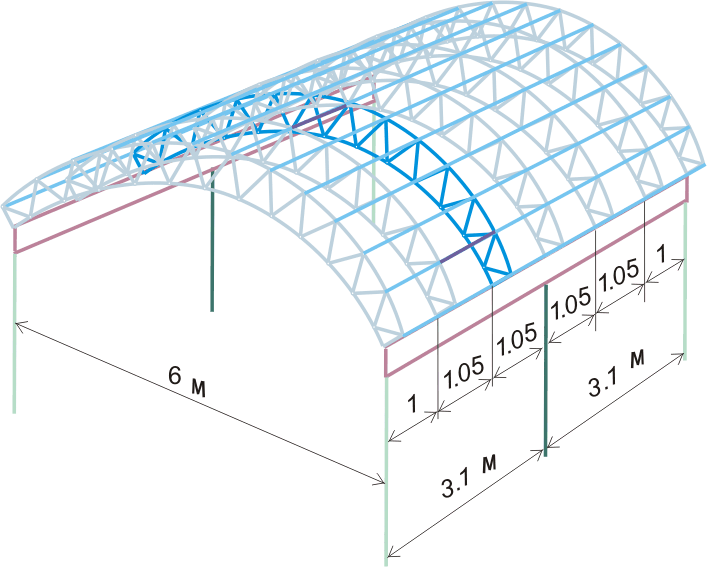
Рисунок 293.1. Общая предварительная схема арочной галереи.
В целом, если изготовление ферм планируется из одного-двух типоразмеров профиля, то расчет такой прямоугольной фермы много времени не займет.
Сосредоточенными нагрузками для данных прямоугольных ферм будут опорные реакции для рассчитывавшихся ранее арочных ферм. Эти нагрузки Q будут приложены в узлах фермы, как показано на рисунке 554.1.б). Общая геометрия фермы показана на рисунке 554.1.а):
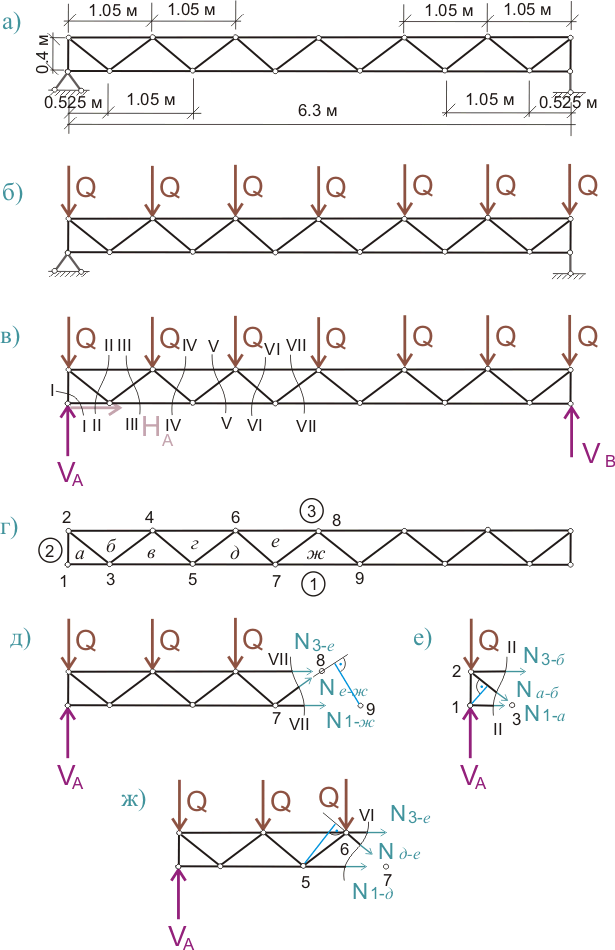
Рисунок 554.1. Общая геометрия и расчетные схемы для прямоугольной фермы.
Для упрощения расчетов длины всех пролетов между узлами в верхнем поясе приняты одинаковыми.
Определение усилий в стержнях фермы
Расчет ферм будет производиться методом сечений, основные положения которого изложены отдельно.
Когда мы рассчитывали арочные фермы, то выяснили, что опорные реакции у этих ферм могут быть разными в зависимости от рассматриваемого варианта снеговой нагрузки. Для дальнейших расчетов примем максимально возможное значение опорных реакций, тогда нагрузки на ферму от арочных ферм будут Q = 796.1 кг.
Кроме того на ферму будет действовать равномерно распределенная нагрузка от собственного веса фермы, к тому же изначально нам не известная, а это означает, что ферму следует дополнительно рассчитать на эту нагрузку. Однако с учетом того, что собственный вес фермы будет относительно небольшой, то для упрощения расчетов эту распределенную нагрузку от собственного веса можно условно привести к сосредоточенным в узлах фермы. Например, если ферма будет весить около 28 кг, то дополнительные сосредоточенные нагрузки составят 28/7 = 4 кг, тогда расчетные нагрузки составят:
Q = 796.1 + 4 ≈ 800 кг
Так как у нас симметричная ферма, к которой одинаковые нагрузки также приложены симметрично, то опорные реакции будут равны между собой и составят:
VA = VB = 7Q/2 = 7·800/2 = 2800 кгс
Значение горизонтальной составляющей опорной реакции на опоре А будет равно нулю, так как горизонтальных нагрузок в нашей расчетной схеме нет, поэтому горизонтальная составляющая реакции на опоре А показана на рисунке 554.1.в) бледно фиолетовым цветом.
Также на рисунке 554.1.в) показаны сечения, по которым можно рассчитать усилия во всех стержнях фермы с учетом симметричности фермы и нагрузок. Далее будет рассматриваться расчет только по 4 сечениям.
Маркировка, показанная на рисунке 554.1.г) означает, что у фермы есть:
Стержни нижнего пояса: 1-а, 1-в, 1-д, 1-ж;
Стержни верхнего пояса: 3-б, 3-г, 3-е;
Стойка: 2-а;
Раскосы: а-б, б-в, в-г, г-д, д-е, е-ж.
При необходимости для маркировки стержней, симметричных указанным, можно использовать апостроф '.
Если стоит задача рассчитать все стержни фермы, то лучше составить таблицу, в которую вносятся все стержни фермы. Затем в эту таблицу будут внесены результаты расчетов, в частности значения сжимающих или растягивающих напряжений.
Во всех сечениях, показанных на рисунке 554.1, силы N направлены так, что вызывают растяжения в рассматриваемых стержнях. Если по результатам расчетов усилие в рассматриваемом стержне будет отрицательным, то это означает, что в этом стержне будут действовать сжимающие нормальные напряжения.
Приступим к рассмотрению сечений.
сечение II-II (рис. 554.1.е)
Составим уравнение моментов относительно узла 3, это позволит определить усилие в стержне 3-б:
М3 = VAl - Ql + N3-бh = 0;
N3-бh =Ql - VAl;
где l - плечо действия силы Q и опорной реакции VA, равное расстоянию от узла 1 до узла 3 по горизонтали, согласно принятой нами расчетной схемы l = 0.525 м; h - плечо действия силы N3-a, равное высоте фермы, в данном случае h = 0.4м. Это означает, что в действительности общая высота фермы с учетом сечений верхнего и нижнего пояса будет немного больше, так как в данном случае высота - это расстояние между нейтральными осями верхнего и нижнего поясов.
Тогда:
N3-б =(Ql - VAl)/h = ((800 - 2800)0.525)/0.4 = - 2625 кг
Чтобы определить напряжения в стержне а-б составим уравнение моментов относительно узла 1:
М1 = Nа-бh' + N3-бh = 0;
Na-б = 2625·0.4/0.318 = 3300.4 кг
В данном случае h' - плечо приложения силы Nа-б - это высота прямоугольного треугольника. Плечо было определено следующим образом, сначала вычисляется значение угла а между стержнями 1-а и а-б.
tga = 0.4/0.525 = 0.762
где 0.4 и 0.525 - длины стержней - катетов прямоугольного треугольника.
a = 37.3°
тогда
h' = 0.525sina = 0.525·0.606 = 0.318 м
Усилия в стержне 1-а будут равны нулю, в чем легко убедиться,составив уравнение моментов относительно узла 2:
М2 =- N1-а·0.4 = 0;
Проверим правильность вычислений, составив уравнения проекций сил на основные оси:
ΣQy = - Q1 +VA - Na-бsin37.3о = -800 +2800 - 3300.4·0.606 = 0.004 кг
ΣQx = N3-б + Na-бсos37.3o = -2625 + 3300.4·0.795 = 0.38 кг
Небольшая погрешность в вычислениях набежала из-за того, что вычисления ведутся с точностью до одного знака после запятой, а в значениях тригонометрических функций указываются только 3-4 знака после запятой. Но в данном случае большая точность и не нужна. В целом при таких нагрузках, на погрешность до 1 кг можно не обращать внимания.
сечение VII-VII (рис. 554.1.д)
Для определения усилий в стержне 1-ж составим уравнение моментов относительно узла 8:
М8 = -Q(1.05 + 2.1 + 3.15) + 3.15VA - 0.4N1-ж = 0;
N1-ж = (-6.3·800 + 3.15·2800)/0.4 = 9450 кг
Для определения усилий в стержне 3-е составим уравнение моментов относительно узла 7:
М7 = -Q(0.525 + 1.575 + 2.625) + 2.625VA + 0.4N3-е = 0;
N3-е = (800·4.725 - 2800·2.625)/0.4 = - 8925 кг (работает на сжатие)
Для определения усилий в стержне е-ж составим уравнение моментов относительно узла 9:
М9 = -Q(1.575 + 2.625 + 3.675) + 3.675VA + 0.4N3-е + 0.636Nе-ж = 0;
Nе-ж = (800·7.875 - 2800·3.675 + 0.4·8925)/0.6363 = - 660 кг
Проверим правильность расчетов
ΣQх = N3-е + N1-ж + Nе-жcos37.3° =- 8925 + 9450 - 660·0.7955 = 0.012 кг
Для лучшего представления общей картины проверим еще пару сечений
сечение VI-VI (рис. 554.1.ж)
Для определения усилий в стержне 1-д составим уравнение моментов относительно узла 6:
М6 = -Q(1.05 + 2.1)+ 2.1VA - 0.4N1-д = 0;
N1-д = (- 3.15·800 + 2.1·2800)/0.4 = 8400 кг
Для определения усилий в стержне д-е составим уравнение моментов относительно узла 5:
М5 = 1.575(-Q + VA)+ 0.4N3-е + 0.6363Nд-е = 0;
Nд-е = (1.575(800 - 2800) + 0.4·8925)/0.6363 = 660 кг
Проверим правильность расчетов, определив проекции сил на ось х:
ΣQx = N3-е + N1-ж + Nд-еcos37.3° = -8925 + 8400 + 660·0.7955 = 0.06 кг;
сечение III-III
Усилия в стержне 3-б нам уже известны, поэтому для определения усилий в стержне б-в составим уравнение моментов относительно узла 5:
М5 = -1.575Q + 1.575VA - 0.4N3-б + 0.6363Nб-в = 0;
Nб-в = (1.575(800 - 2800) + 0.4·2625)/0.6363 = -3300.4 кг
Усилие в стержне 1-в будет явно значительно меньше, чем в стержне 1-ж и потому в данном случае оно нас не интересует, так как мы планируем делать нижний пояс из трубы одного сечения. А чтобы определить правильность расчетов в данном случае определим проекции сил на ось у:
ΣQy = - Q1 +VA + Nб-вsin37.3о = -800 +2800 - 3300.4·0.606 = 0.04 кг
Теперь у нас есть все основные данные для дальнейшего расчета
Подбор сечения
На первый взгляд самым загруженным является стержень нижнего пояса 1-ж, на который действует продольная растягивающая сила N1-ж = 9450 кг. Однако напряжения в сжатом стержне 3-е в результате продольного изгиба могут быть даже больше, поэтому в первую очередь проверим прочность именно этого стержня по следующей формуле:
σ = N/φF ≤ R
где φ - коэффициент продольного изгиба, F - площадь сечения профиля, см, R - расчетное сопротивление материала профиля. Если расчетное сопротивление стали зараннее не известно, то для надежности рекомендуется принимать одно из минимальных R = 2300 кг/см2.
Расчет сжатых стержней ничем не отличается от расчета колонн, поэтому далее приводятся только основные этапы расчета без подробных пояснений.
по таблице 1 (см. ссылку выше) определяем значение μ = 1, это значение будет наиболее оптимальным с учетом рекомендаций нормативных документов, в частности СНиП II-23-81*(1990) "Стальные конструкции", а также того, что основные нагрузки к ферме приложены именно в узлах.
Предварительно определим площадь сечения профиля. Для растянутого стержня 1-ж эта площадь составит:
F = N/R = 9450/2300 = 4.11 см2
По сортаменту для прямоугольных профильных труб этому требованию удовлетворяет труба сечением 50х30х3 мм, площадь сечения такой трубы составит F = 4.21 см2, минимальный радиус инерции i = 1.16 см. Проверим, подходит ли эта труба для сжатого верхнего пояса фермы, так как делать пояса из труб разного сечения - дополнительное усложнение технологии, мало оправданное при таких малых объемах работ, всего-то нужно сделать 2 фермы.
При радиусе инерции i = 1.14 см, значение коэффициента гибкости составит
λ = μl/i = 1·105/1.16 = 90.5 ≈ 90
тогда по таблице 2 коэффициент изгиба φ = 0.629 (определяется интерполяцией значений 2050 и 2450)
8925/(0.629·4.21) = 3368 кгс/см2 >> R = 2300 кгс/см2;
Как видим, такое значение напряжений значительно больше допустимого. Если для изготовления поясов использовать трубу 50х40х3 мм, имеющую площадь сечения 4.81 см и минимальный радиус инерции i = 1.54 см, то результат расчетов будет следующим:
λ = 1·105/1.54 = 68.2 ≈ 68
φ = 0.77
8925/(0.77·4.81) = 2409 кгс/см2 > R = 2300 кгс/см2;
Как видим и такой трубы для обеспечения прочности не достаточно. Ну а дальше возможны разные варианты, можно для изготовления поясов использовать трубу 50х40х3.5 мм с площадью сечения 5.49 см2, которая явно обеспечит требуемый запас прочности, можно рассматривать и другие варианты, но мы остановимся на этом.
Теперь нужно проверить максимально допустимую гибкость для растянутого пояса из плоскости фермы. Согласно СНиП II-23-81* "Стальные конструкции" эта гибкость для растянутых элементов ферм не должна превышать 400. Соответственно трубы при изготовлении нужно располагать так, чтобы 50 - это была ширина трубы, а не высота, тогда при радиусе i = 1.81 см гибкость нижнего пояса составит:
λ = 1·630/1.81 = 348
Это требование нами соблюдено, можно переходить к расчету раскосов и стоек. Наиболее нагруженным раскосом будет сжатый стержень б-в. Его расчетная длина составит:
l = 0.525/cos37.3° = 0,525/0.7954 = 0.66 м или 66 см
Для соседнего растянутого раскоса, при заданном расчетном сопротивлении для обеспечения прочности потребуется труба сечением не менее
F = N/R = 3300.4/2300 = 1.43 см2
Для сжатого раскоса с учетом возможного продольного изгиба сечение должно быть больше, насколько именно - неизвестно, но мы теперь ученые и потому сразу примем трубу с хорошим запасом по площади сечения.
Для начала проверим квадратную трубу 25х25х2.5 мм, имеющую сечение 2.14 см2, радиус инерции i = (1.77/2.14)1/2 = 0.91 см. Тогда:
λ = 1·66/0.91 = 72.6
φ = 0.74
3300.4/(0.74·2.14) = 2084 кгс/см2 < R = 2300 кгс/см2;
Данная труба удовлетворяет требованиям и даже с некоторым запасом. Осталось выяснить какова будет примерно общая масса фермы:
m = 1.41(0.66·12 + 0.4·2) + 4.31·6.3·2 = 66.6 кг
Это в 2 раза больше, чем мы предположили вначале, но в целом общее увеличение нагрузки с учетом собственного веса фермы будет очень незначительным, около 0.6%.
Тем не менее поиск оптимального варианта можно продолжать, в данной статье остановимся на том, что есть.
Все необходимые условия по прочности и устойчивости нами соблюдены, но при этом никто не запрещает использовать для изготовления ферм профили большего сечения.
Осталось рассчитать длины и катеты сварных швов, но это уже отдельная тема. | 
