Расчет квадратной плиты, опертой по контуру, на действие сосредоточенной нагрузки посередине

Необходимость в таком расчете появляется тогда, когда на плиту (пластину), опертую по контуру, устанавливается колонна или какая другая стойка. Если проектируемая плита будет железобетонной, то конечно же лучше всего предусмотреть усиление арматурой места приложения сосредоточенной нагрузки, а то и вовсе сделать ребра в плите.

Однако иногда необходимость установить колонну появляется уже после того, как железобетонная плита изготовлена. Да и материал плиты (пластины) может быть любым. Для упрощения рассмотрим случай, когда на стальную квадратную пластину, имеющую шарнирное опирание по контуру, устанавливается стальная стойка.

Но начнем, как ни странно с дерева. Чтобы хотя бы примерно понять, что там в этой пластине происходит.

Итак есть у нас помещение размерами 5х5 м. Посредине планируется поставить стоку кровли, которая будет давать нагрузку Q. Укладываем две деревянные балки одинакового сечения крест на крест. В итоге (так как балки прогнутся на одинаковую величину) получаем следующие расчетные моменты:

М_х = М_у = Ql/2·4 = 0.125Ql (724.1)

Например по расчету требуется сечение 10х20 см. Момент сопротивления такого сечения W = 10·20²/6 = 666.67 см³.

 Тогда пластина с таким же моментом сопротивления, но шириной 500 см будет иметь высоту:

h = (6W/b)^1/2 = (6·666.67/500)^1/2 = 2.83 см (724.2)

Вот только пластина - это не балка. Если посмотреть на эпюру моментов в балке от сосредоточенной нагрузки:

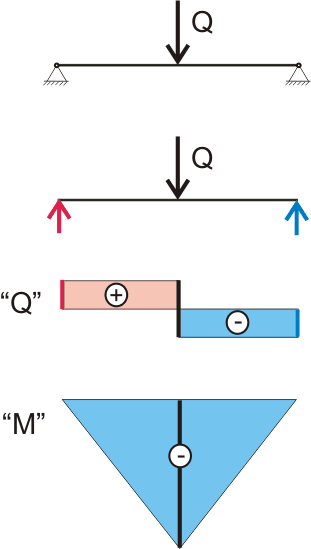
Рисунок 149.7.1

То кроме всего прочего эта эпюра является также диаграммой эффективности использования материала пластины. Т.е. когда у нас имеется балка и на балку действует сосредоточенная сила, то эффективность использования материала балки, условно говоря, равна 100 %, а когда такая же сосредоточенная сила приложена к пластине, то эффективность использования материала снижается в 2 раза, т.к. площадь эпюры момента в 2 раза меньше площади прямоугольника.

Исходя из этого можно предположить, что при расчетах квадратных пластин на сосредоточенную нагрузку расчетное значение моментов в взаимно перпендикулярных плоскостях будет составлять:

М_х = М_у = 2Ql/2·4 = Ql/4 = 0.25Ql (724.3)

Пример упрощенного расчета стальной пластины на сосредоточенную нагрузку

Дано: на пластину размерами 0.9х0.9 м с шарнирным опиранием по контуру действует сосредоточенная сила посредине Q = 5067 кг.

Требуется: определить толщину пластины.

Решение:

Согласно формуле (724.3):

М_х = М_у = Ql/4 = 5067·0.9/4 =  1140.1 кгм (724.4)

Так как в пластине возникает плоское напряженное состояние, то расчетный момент составит:

М = Мх√2 = 1140.1·1.41 = 1612.3 кгм или 161230 кгсм (724.5)

При расчетном сопротивлении стали R_s = 2350 кг/см² требуемый момент сопротивления составит:

W_тр = M/R_s = 161230/2350 = 68.6 см³ (724.6)

требуемая толщина листа:

h = (6W/b)^1/2 = (6·68.6/90)^1/2 = 2.14 см (724.2)

По сортаменту принимаем для пластины листовую сталь толщиной 22 мм.

Примечание: Специальных таблиц, где рассматривается сила, условно сосредоточенная в одной точке, я не знаю. Если воспользоваться таблицами Вайнбергов, то для случая, когда сила распределяется на участке, равном 1/10 от ширины (длины) квадратной пластины, т.е. в данном случае на участке размерами 9х9 см, расчетный коэффициент для определения момента по таблице III.8 составит k₂ = k₃ = 0.284. Соответственно изгибающий момент М_х = 0.284Q = 1439 кгм, т.е. в 1.26 раза больше. 

А если воспользоваться теми же таблицами Вайнбергов для равномерно распределенной нагрузки, то переведя сосредоточенную нагрузку в эквивалентную плоскую равномерно распределенную, получим:

q_экв = 4Q/l² = 4·5067/0.9² = 25022 кг/м²

k₂ = k₃ = 0.0479

M_x = M_y = k₂q_эквl² = 1198.5 кгм

т.е. в 1.05 раза больше, чем при упрощенном расчете.

Тем не менее этот результат я считаю более правильным. Если пересчитать требуемую толщину листа по этому значению момента, то требуемая толщина составит 2.19 см.

Пример определения допустимой сосредоточенной нагрузки на плиту

Дано: квадратная железобетонная плита перекрытия с шарнирным опиранием по контруру размерами 5х5 метров, рассчитанная на равномерно распределенную нагрузку 800 кг/м² с учетом собственного веса плиты. Расчетная равномерно распределенная нагрузка на плиту 300 кг/м².

Требуется: определить допустимую сосредоточенную нагрузку на плиту от колонны, устанавливаемой по центру плиты.

Решение:

Допустимая равномерно распределенная нагрузка на плиту составит:

q = 800 - 300 = 500 кг/м²

Допустимая сосредоточенная нагрузка на плиту составит:

Q = ql²/4 = 500·5²/4 = 3125 кг

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

На главную

• Расчет конструкций ::: Основы строймеха и сопромата ::: Пластины

Комментариев нет

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).