1 вариант
Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно расстоянию между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки также попадают на начало и на конец пролета, но при этом вызывают только увеличение опорной реакции, на значение изгибающих моментов и на прогиб крайние сосредоточенные нагрузки никак не влияют, а потому при расчетах несущей способности конструкции не учитываются. Рассмотрим это на примере балок перекрытия опирающихся на перемычку. Кирпичная кладка, которая может быть между перемычкой и балками перекрытия, и создавать при этом равномерно распределенную нагрузку, для простоты восприятия не показана.
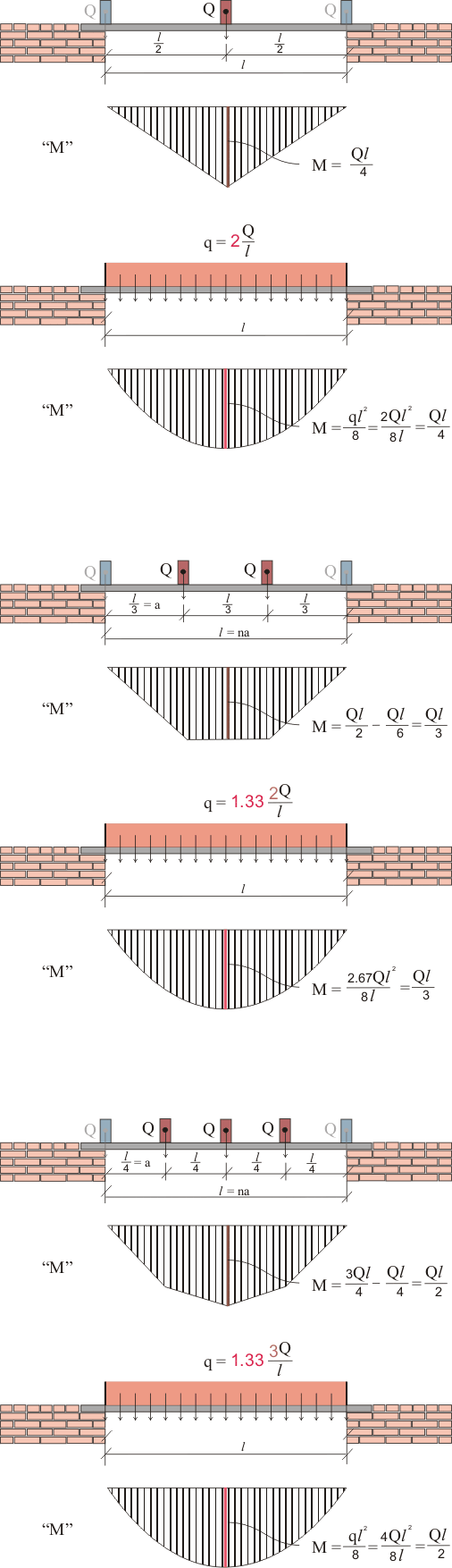
Рисунок 1. Приведение сосредоточенных нагрузок к эквивалентной равномерно распределенной нагрузке.
Как видно из рисунка 1, определяющим является изгибающий момент, который используется при расчетах конструкций на прочность. Таким образом, чтобы равномерно распределенная нагрузка создавала такой же изгибающий момент, как и сосредоточенная нагрузка, ее нужно умножить на соответствующий коэффициент перехода (коэффициент эквивалентности). А определяется этот коэффициент из условий равенства моментов. Думаю, рисунок 1 это очень хорошо иллюстрирует. А еще, анализируя полученные зависимости, можно вывести общую формулу для определения коэффициента перехода. Так, если количество приложенных сосредоточенных нагрузок является нечетным, т.е. одна из сосредоточенных нагрузок обязательно попадает на середину пролета, то для определения коэффициента эквивалентности можно использовать формулу:
γ = n/(n - 1) (305.1.1)
где n - количество пролетов между сосредоточенными нагрузками.
При этом эквивалентная равномерно распределенная нагрузка будет равна:
qэкв = γ(n-1)Q/l (305.1.2)
где (n-1) - количество сосредоточенных нагрузок.
Впрочем, иногда удобнее производить расчеты, исходя из количества сосредоточенных нагрузок. Если это количество выразить переменной m, то тогда
γ = (m +1)/m (305.1.3)
где m - количество сосредоточенных нагрузок.
При этом эквивалентная равномерно распределенная нагрузка будет равна:
qэкв = γmQ/l (305.1.4)
Когда количество сосредоточенных нагрузок является четным, т.е. ни одна из сосредоточенных нагрузок не попадает на середину пролета, то значение коэффициента можно принимать, как для следующего нечетного значения количества сосредоточенных нагрузок. В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:
γ = 2 - если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки.
γ = 1.33 - для балки, на которую действуют 2 или 3 сосредоточенные нагрузки;
γ = 1.2 - для балки, на которую действуют 4 или 5 сосредоточенных нагрузок;
γ = 1.142 - для балки, на которую действуют 6 или 7 сосредоточенных нагрузок;
γ = 1.11 - для балки, на которую действуют 8 или 9 сосредоточенных нагрузок.
2 вариант
Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно половине расстояния между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки не попадают на начало и на конец пролета.
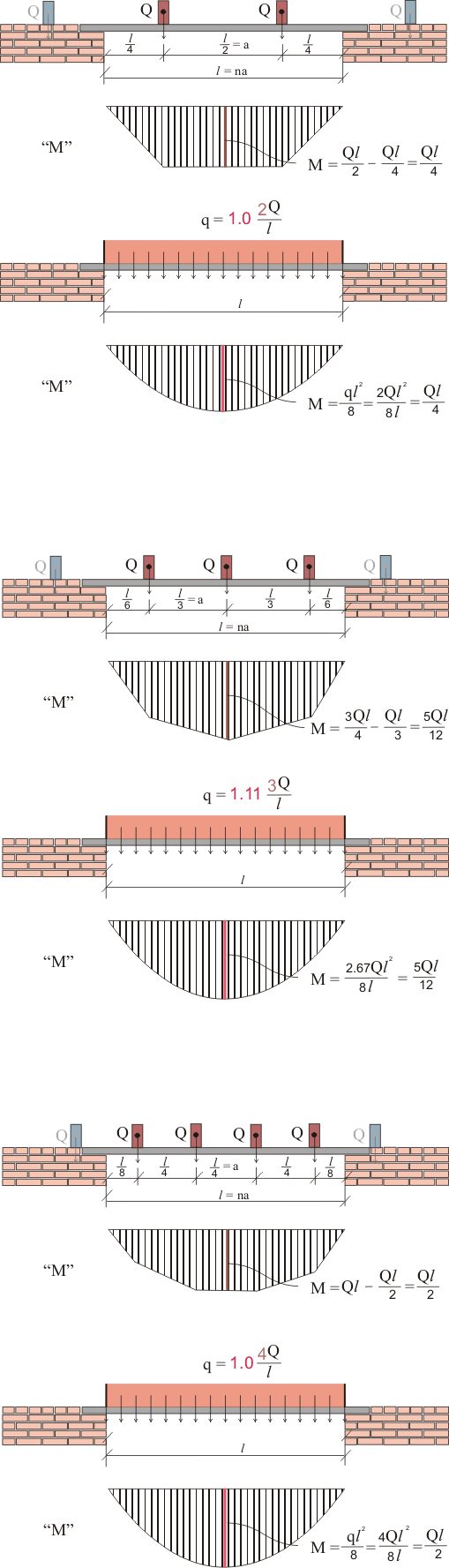
Рисунок 2. Значения коэффициентов перехода при 2 варианте приложения сосредоточенных нагрузок.
Как видно из рисунка 2, при таком варианте загружения значение коэффициента перехода будет значительно меньше. Так, например, при четном количестве сосредоточенных нагрузок, коэффициент перехода вообще можно принимать равным единице. При нечетном количестве сосредоточенных нагрузок для определения коэффициента эквивалентности можно использовать формулу:
γ = (m +7)/(m +6) (305.2.1)
где m - количество сосредоточенных нагрузок.
При этом эквивалентная равномерно распределенная нагрузка все также будет равна:
qэкв = γmQ/l (305.1.4)
В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:
γ = 2 - если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки, а попадают ли балки перекрытия на начало или конец пролета или расположены сколь угодно далеко от начала и конца пролета, в данном случае значения не имеет. А значение это имеет при определении сосредоточенной нагрузки.
γ = 1 - если на рассматриваемую конструкцию, действует четное количество нагрузок.
γ = 1.11 - для балки, на которую действуют 3 сосредоточенные нагрузки;
γ = 1.091 - для балки, на которую действуют 5 сосредоточенных нагрузок;
γ = 1.076 - для балки, на которую действуют 7 сосредоточенных нагрузок;
γ = 1.067 - для балки, на которую действуют 9 сосредоточенных нагрузок.
Не смотря на некоторую заковыристость определения, коэффициенты эквивалентности очень просты и удобны. Так как при расчетах очень часто известна распределенная нагрузка, действующая на квадратный или погонный метр, то чтобы не переводить распределенную нагрузку сначала в сосредоточенную, а потом снова в эквивалентную распределенную, достаточно просто умножить значение распределенной нагрузки на соответствующий коэффициент. Например, на перекрытие будет действовать нормативная распределенная нагрузка 400 кг/м2, при этом собственный вес перекрытия составит еще 300 кг/м2. Тогда при длине балок перекрытия 6 м на перемычку могла бы действовать равномерно распределенная нагрузка q = 6(400 + 300)/2 = 2100 кг/м. А дальше, если будет только одна балка перекрытия посредине пролета, то γ = 2, а
qэкв = γq = 2q (305.2.2)
И все.
Если ни одно из двух вышеприведенных условий не соблюдается, то использовать коэффициенты перехода в чистом виде нельзя, нужно добавить еще пару дополнительных коэффициентов, учитывающих расстояние до балок, не попадающих на начало и конец пролета перемычки, а также возможную несимметричность приложения сосредоточенных нагрузок. Вывести такие коэффициенты в принципе можно, однако в любом случае они будут понижающими во всех случаях, если рассматривать 1 вариант загружения и в 50% случаев, если рассматривать 2 вариант загружения, т.е. значения таких коэффициентов будут < 1. А потому для упрощения расчетов, а заодно и для большего запаса по прочности рассчитываемой конструкции вполне хватит коэффициентов, приведенных при первых двух вариантах загружения. | 
