Пример расчета треугольной фермы

При расчете промышленных ферм, перекрывающих большие пролеты и работающих под большими нагрузками, может использоваться до 10-15 видов сечений, точнее профилей с различными параметрами сечения. Это связано с тем, что напряжения в стержнях фермы разные и потому максимально точный подбор сечения при промышленных объемах производства ферм дает ощутимую экономию. В частном же строительстве при изготовлении ферм используются 1-2, максимум 3 вида сечений, не только из экономических, но и из эстетических соображений и потому достаточно рассчитать максимально нагруженные стержни и по этим показателям принимать сечение для остальных стержней фермы. В общем виде это может выглядеть примерно так:

Имеется открытая площадка размерами 10х5 м возле дома и эту площадку хочется сделать закрытой, чтобы летом можно было пить чай на улице, не взирая на погодные условия, точнее взирая, но из-под надежного навеса, а еще чтобы можно было поставить машину под навес, сэкономив на гараже, да и вообще чтобы была защита от солнечного зноя в летний день. Вот только 10 метров - пролет большой и балку для такого пролета подобрать трудно, да и слишком массивной будет эта самая балка - скучно и вообще напоминает заводской цех. В таких случаях оптимальный вариант - сделать вместо балок фермы, а потом уже по фермам кидать обрешетку и делать кровлю. Само собой форма фермы может быть любой, но далее будет рассматриваться расчет треугольной фермы, как наиболее простой вариант. Проблемы расчета колонн для подобного навеса рассматриваются отдельно, расчет двух ферм с параллельными поясами или ригелей, на которые будут опирать фермы, здесь также не приводится.

Пока предполагается, что фермы будут располагаться с шагом 1 метр, а нагрузка на ферму от обрешетки будет передаваться только в узлах фермы. Кровельным материалом будет служить профнастил. Высота фермы может быть теоретически любой, вот только если это навес, примыкающий к основному зданию, то главным ограничителем будет форма кровли, если здание одноэтажное, или окна второго этажа, если этажей больше, но в любом случае сделать высоту фермы больше 1 м вряд ли получится, а с учетом того, что надо делать еще и ригеля между колоннами, то и 0.8 м не всегда выйдет (тем не менее примем эту цифру для расчетов). На основании этих предположений уже можно конструировать ферму:

Рисунок 272.1. Общая предварительная схема навеса по фермам.

На рисунке 272.1 голубым цветом показаны балки обрешетки, синим цветом - ферма, которую следует рассчитать, фиолетовым цветом - балки или фермы, на которые опираются колонны, изменение цвета от светло-голубого к темно-фиолетовому в данном случае показывает увеличение расчетной нагрузки, а значит для для более темных конструкций потребуются более мощные профили. Фермы на рисунке 272.1 показаны темно-зеленым цветом из-за совершенно иного характера нагрузки. Таким образом расчет всех элементов конструкции по отдельности, как то:

- стальных листов профнастила

- балок обрешетки (балки обрешетки можно рассматривать как многопролетные балки, если длина балок будет около 5 м, если балки будут делаться длиной около 1 м, т.е. между фермами, тогда это обычные однопролетные балки на шарнирных опорах) 

- ферм кровли (достаточно определить нормальные напряжения в поперечных сечениях стержней, о чем речь ниже)

- балок или ферм под фермами кровли (рассчитываются как однопролетные балки или фермы)

- колонн

никаких особых проблем не представляет. Однако целью данной статьи является показать пример расчета именно треугольной фермы, этим мы и займемся. На рисунке 272.1 можно рассмотреть 6 треугольных ферм, при этом на крайние (переднюю и заднюю) фермы нагрузка будет в 2 раза меньше, чем на остальные фермы. Это означает, что эти две фермы если есть стойкое желание сэкономить на материалах, следует рассчитывать отдельно. Однако из эстетических и технологических соображений лучше все фермы сделать одинаковыми, а это значит, что достаточно рассчитать все лишь одну ферму (показана на рис.272.1 синим цветом). В данном случае ферма будет консольной, т.е. опоры фермы будут располагаться не на концах фермы, а в узлах, показанных на рисунке 272.2. Такая расчетная схема позволяет более равномерно распределить нагрузки, а значит, и использовать для изготовления ферм профили меньшего сечения. Для изготовления ферм планируется использовать квадратные профильные трубы одного типа, а подобрать требуемое сечение профильной трубы поможет дальнейший расчет.

Если балки обрешетки будут опираться сверху на узлы ферм, то нагрузку от навеса из профнастила и снега лежащего на этом профнастиле, можно считать сосредоточенной, приложенной в узлах фермы. Стержни фермы будут свариваться между собой, при этом стержни верхнего пояса скорее всего будут неразрезными длиной примерно 5.06 м. Однако будем считать, что все узлы фермы - шарнирные. Эти уточнения могут показаться незначительной мелочью, однако позволяют максимально ускорить и упростить расчет, по причинам, изложенным в другой статье. Единственное, что нам осталось определить для дальнейших расчетов, сосредоточенную нагрузку, но и это сделать не сложно, если профнастил или балки обрешетки уже рассчитаны. При расчете профнастила мы выяснили, что листы профнастила длиной 5.1-5.3 м представляют собой многопролетную неразрезную балку с консолью. Это означает, что опорные реакции для такой балки и соответственно нагрузки для нашей фермы будут не одинаковыми, однако изменения опорных реакций для 5 пролетной балки будут не такими уж и значительными и для упрощения расчетов можно считать, что нагрузка от снега, профнастила и обрешетки будет передаваться равномерно, как в случае с однопролетными балками. Такое допущение приведет только к небольшому запасу по прочности. В итоге мы получаем следующую расчетную схему для нашей фермы:

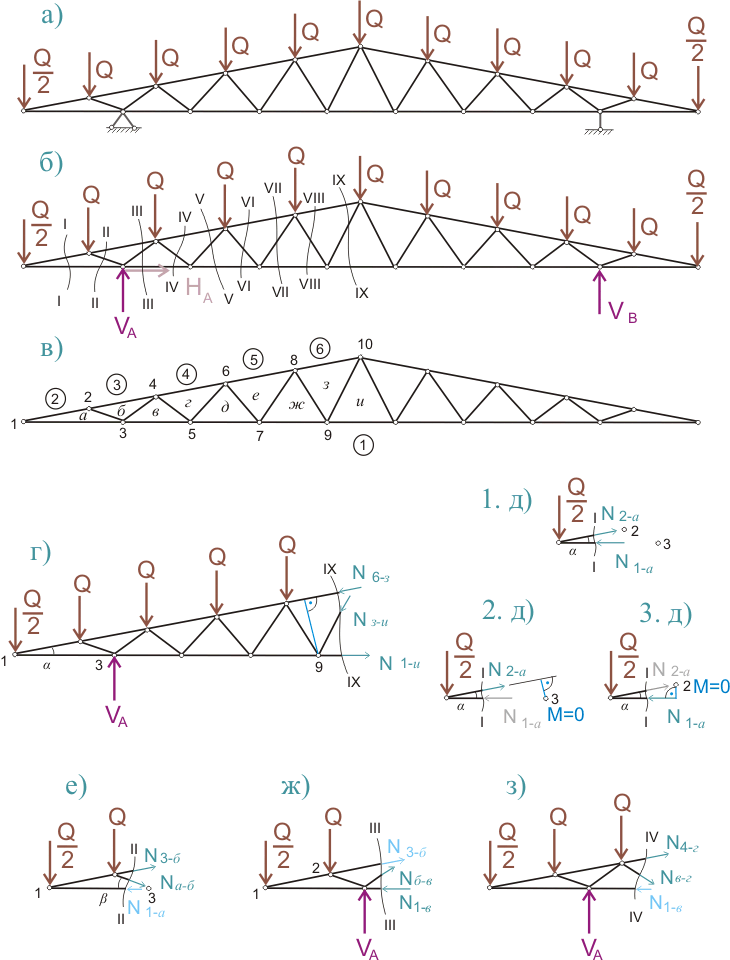
Рисунок 272.2. Расчетная схема для треугольной фермы.

На рисунке 272.2 а) представлена общая расчетная схема нашей фермы, расчетная нагрузка составляет Q = 190 кг, что вытекает из расчетной снеговой нагрузки 180 кг/м², веса профнастила и возможного веса балки обрешетки. На рисунке 272.2 б) показаны сечения, благодаря которым можно рассчитать усилия во всех стержнях фермы с учетом того что ферма и нагрузка на ферму является симметричной и значит достаточно рассчитывать не все стержни фермы, а чуть больше половины. А чтобы не запутаться во многочисленных стержнях при расчете, стержни и узлы ферм принято маркировать. Маркировка, показанная на рис.272.2 в) означает, что у фермы есть:

Стержни нижнего пояса: 1-а, 1-в, 1-д, 1-ж, 1-и;

Стержни верхнего пояса: 2-а, 3-б, 4-г, 5-е, 6-з;

Раскосы: а-б, б-в, в-г, г-д, д-е, е-ж, ж-з, з-и.

Если будет рассчитываться каждый стержень фермы, то желательно составить таблицу, в которую следует внести все стержни. Затем в эту таблицу будет удобно вносить полученное значение сжимающих или растягивающих напряжений.

Ну а сам расчет никаких особенных сложностей не представляет, если ферма будет свариваться из 1-2 видов профилей замкнутого сечения. Например, весь расчет фермы можно свести к тому, чтобы рассчитать усилия в стержнях 1-и, 6-з и з-и. Для этого достаточно рассмотреть продольные силы, возникающие при отсечении части фермы по линии IX-IX (рис. 272.2 г).

Но оставим сладкое на третье, и посмотрим как это делается на более простых примерах, для этого рассмотрим

сечение I-I (рис. 272.2.1 д)

Если указанным образом отсечь лишнюю часть фермы, то нужно определить усилия только в двух стержнях фермы. Для этого используются уравнения статического равновесия. Так как в узлах фермы шарниры, то и значение изгибающих моментов в узлах фермы равно нулю, а кроме того, исходя из тех же условий статического равновесия сумма всех сил относительно оси х или оси у также равна нулю. Это позволяет составить как минимум три уравнения статического равновесия (два уравнения для сил и одно для моментов), но в принципе уравнений моментов может быть столько же сколько узлов в ферме и даже больше, если использовать точки Риттера. А это такие точки в которых пересекаются две из рассматриваемых сил и при сложной геометрии фермы точки Риттера не всегда совпадают с узлами фермы. Тем не менее в данном случае у нас геометрия достаточно простая (до сложной геометрии мы еще успеем добраться) и потому для определения усилий в стержнях достаточно имеющихся узлов фермы. Но при этом опять же из соображений простоты расчета обычно выбираются такие точки, уравнение моментов относительно которой позволяет сразу определить неизвестное усилие, не доводя дело до решения системы из 3 уравнений.

Выглядит это примерно так. Если составить уравнение моментов относительно точки 3 (рис. 272.2.2 д), то в нем будут всего два члена, причем один из них уже известный:

М₃ = -Ql/2 + N_2-ah = 0;

N_2-ah = Ql/2;

где l - расстояние от точки 3 до точки приложения силы Q/2, которое в данном случае и является плечом действия силы, согласно принятой нами расчетной схемы l = 1.5 м; h- плечо действия силы N_2-a (плечо показано на рис. 272.2.2 д) синим цветом).

При этом третий возможный член уравнения равен нулю, так как сила N_1-а (на рис. 272.2.2 д) показана серым цветом) направлена по оси, проходящей через точку 3 и значит плечо действия равно нулю. Единственное, что в этом уравнении нам неизвестно - это плечо действия силы N_2-а, впрочем определить его, владея соответствующими знаниями по геометрии, легко.

Наша ферма имеет расчетную высоту 0.8 м и общую расчетную длину 10 м. Тогда тангенс угла α составит tgα = 0.8/5 = 0.16, соответственно значение угла α = arctgα = 9.09^о. И тогда

h = lsinα

Теперь нам ничего не мешает определить значение силы N_2-a:

N_2-a = Ql/(2lsinα) = 190/(2·0.158) = 601.32 кг

Подобным же образом определяется значение N_1-а. Для этого составляется уравнение моментов относительно точки 2:

М₂ = -Ql/2 + N_1-ah = 0;

N_1-ah = Ql/2

N_1-a = Q/(2tgα) = 190/(2·0.16) = 593.77 кг

Проверить правильность вычислений мы можем, составив уравнения сил:

ΣQ_y = Q/2 - N_2-asinα = 0; Q/2 = 95= 601.32·0.158 = 95 кг

ΣQ_x = N_2-acosα - N_1-a = 0; N_1-a = 593.77 = 601.32·0.987 = 593.77 кг

Условия статического равновесия выполняются и любое из уравнений сил, использованных для проверки, можно было использовать для определения усилий в стержнях. Вот, собственно и все, дальнейший расчет фермы - чистейшая механика, но на всякий случай рассмотрим еще 

сечение II-II (рис. 272.2. e)

На первый взгляд кажется, что более простым будет уравнение моментов относительно точки 1 для определения силы N_а-б, однако в этом случае потребуется для определения плеча силы сначала найти значение угла β. А вот если рассматривать равновесие системы относительно точки 3, то:

М₃ = -Ql/2 - Ql/3 + N_3-бh = 0;

 N_3-бh = 5Ql/6;

N_3-б = 5Q/(6sinα) = 5·190/(6·0.158) = 1002.2 кг (работает на растяжение)

Ну а теперь все же определим значение угла β. Исходя из того, что известны все стороны некоего прямоугольного треугольника (нижний катет или длина треугольника - 1 м, боковой катет или высота треугольника - 0.16 м, гипотенуза - 1.012 м и даже угол α), то соседний прямоугольный треугольник с высотой 0.16 м и длиной 0.5 м будет иметь tgβ = 0.32 и соответственно угол между длиной и гипотенузой β = 17.744^о, полученный из арктангенса.  И теперь проще составить уравнение сил относительно оси х:

ΣQ_x = N_3-бcosα + N_а-бcosβ- N_1-а = 0;

N_a-б = (N_1-а - N_3-бcosα)/cosβ = (593.77 - 1002.2·0.987)/ 0.952 = - 415.61 кг

В данном случае знак "-" показывает, что сила направлена в сторону, противоположную от той, которую мы приняли при составлении расчетной схемы. И тут пришло время поговорить о направлении сил, точнее, о том значении, которое в это направление вкладывается. Когда мы заменяем внутренние усилия в рассматриваемом поперечном сечении стержней фермы, то под силой направленной от поперечного сечения подразумеваются растягивающие напряжения, если сила направлена к поперечному сечению, то подразумеваются сжимающие напряжения. С точки зрения статического равновесия не важно какое направление силы принимать при расчетах, если сила будет направлена в противоположную сторону, то значит у этой силы будет знак минус. Однако при расчете важно знать, на какое именно усилие рассчитывается данный стержень. Для растягиваемых стержней принцип определения необходимого сечения простейший:

σ = N/F ≤ R

При расчете стержней, работающих на сжатие, следует учитывать множество различных факторов и в общем виде формулу для расчета сжатых стержней можно выразить так:

σ = N/φF ≤ R

Примечание: расчетную схему можно составлять так, чтобы все продольные силы были направлены от поперечных сечений. В этом случае знак "-" перед значением силы, полученный при расчетах, будет показывать, что данный стержень работает на сжатие.

Так результаты предыдущего расчета показывают, что в стержнях 2-а и 3-б возникают растягивающие напряжения, в стержнях 1-а и а-б - сжимающие усилия. Ну а теперь вернемся к цели нашего расчета - определению максимальных нормальных напряжений в стержнях. Как и в обычной симметричной балке, у которой максимальные напряжения при симметричной нагрузке возникают в сечении, наиболее удаленном от опор, в ферме максимальные напряжения возникают в стержнях наиболее удаленных от опор, т.е. в стержнях, отсекаемых сечением IX-IX.

сечение IX-IX (рис. 272.2. г)

М₉ = -4.5Q/2 - 3.5Q - 2.5Q - 1.5Q -0.5Q + 3V_A - 4.5N_6-зsinα = 0;

N_6-з = (15Q - 10.25Q)/(4.5sinα) = 4.75·190/(4.5·0.158) = 1269.34 кг (работает на сжатие)

где V_A = 5Q, определяются опорные реакции ферм все по тем же уравнениям равновесия системы, так как ферма и нагрузки симметричные, то

V_A = ΣQ_y/2 = 5Q;

так как горизонтальных нагрузок у нас пока не предусмотрено, то горизонтальная опорная реакция на опоре А будет равна нулю, поэтому H_A показано на рисунке 272.2 б) светло фиолетовым цветом.

плечи у всех сил в данном случае разные, а потому сразу подставлены числовые значения плеч в формулу.

Чтобы определить усилие в стержне з-и, нужно сначала определить значение угла γ (на рисунке не показан). Исходя из того, что известны две стороны некоего прямоугольного треугольника (нижний катет или длина треугольника - 0.5 м, боковой катет или высота треугольника - 0.8 м, то tgγ = 0.8/0.5 = 1.6 и значение угла γ = arctgγ = 57.99^о. И тогда для точки 3

h = 3sinγ = 2.544 м. Тогда:

М₃ = - 1.5Q/2 - 0.5Q + 0.5Q + 1.5Q + 2.5Q - 1.5N_6-зsinα + 2.544N_з-и = 0;

N_з-и = (1.25Q - 4.5Q + 1.5N_6-зsinα)/2.544 = (332.5 - 617.5)/2.544 = -112 кг

И теперь проще составить уравнение сил относительно оси х:

ΣQ_x = - N_6-зcosα - N_з-иcosγ + N_1-и = 0;

N_1-и = N_6-зcosα + N_з-иcosγ= 1269.34·0.987 - 112·0.53 = 1193.46 кг (работает на растяжение)

Так как верхний и нижний пояса фермы будут из одного типа профиля, то тратить время и силы на расчет стержней нижнего пояса 1-в, 1-д и 1-ж, равно как и стержней верхнего пояса 4-г и 5-е нет необходимости. Усилия в этих стержнях будут явно меньше уже определенных нами. Если бы ферма была бесконсольной, т.е. опоры располагались на концах фермы, то усилия в раскосах также были бы меньше уже определенных нами, однако у нас ферма с консолями и потому воспользуемся еще несколькими сечениями, чтобы определить усилия в раскосах по приведенному выше алгоритму (подробности расчета не приводятся):

N_б-в = -1527.34 кг - работает на сжатие (сечение III-III, рис.272.2 ж), определялось по уравнению моментов относительно точки 1)

N_в-г = 634.43 кг - работает на растяжение (сечение IV-IV, рис.272.2 з), определялось по уравнению моментов относительно точки 1)

N_г-д = - 493.84 кг - работает на сжатие (сечение V-V, определялось по уравнению моментов относительно точки 1)

Таким образом самыми загруженными у нас являются два стержня N_6-з = 1269.34 кг и N_б-в = - 1527.34 кг. Оба стержня работают на сжатие и если вся ферма будет изготавливаться из одного типа профиля, то достаточно рассчитать один из этих стержней по предельным напряжениям и на основе этих расчетов подобрать необходимое сечение профиля. Однако тут все не так просто, на первый взгляд кажется, что достаточно рассчитать стержень N_б-в, но при расчете сжатых элементов большое значение имеет расчетная длина стержня. Так длина стержня N_6-з составляет 101.2 см, в то время как длина стержня N_б-в составляет 59.3 см. Поэтому, чтобы не гадать, лучше рассчитать оба стержня.

стержень N_б-з

Расчет сжатых стержней ничем не отличается от расчета центрально сжатых колонн, поэтому далее приводятся только основные этапы расчета без подробных пояснений.

по таблице 1 (см. ссылку выше) определяем значение μ = 1 (не смотря на то, что верхний пояс фермы будет из цельного профиля, расчетная схема фермы подразумевает шарнирное закрепление стержней в узлах фермы, поэтому более правильным будет принять вышеуказанное значение коэффициента).

Принимаем предварительно значение λ = 90, тогда по таблице 2 коэффициент изгиба φ = 0.625 (для стали С235 прочностью R_y = 2350 кгс/см², определяется интерполяцией значений 2050 и 2450)

Тогда требуемый радиус инерции составит:

i = μl/λ = 101.2/90 = 1.125 см

По сортаменту для квадратных профильных труб этим условиям удовлетворяет профиль 30х30х2 мм с площадью сечения F = 2.17 см² (радиус инерции i = √(I/F) = 1.133 см), осталось проверить этот профиль на устойчивость:

1269.34/(0.625·2.17) = 935.92 кгс/см² < R_y = 2350 кгс/см²;

Примечание: Если расчетное сопротивление профильной трубы, которая будет использоваться для изготовления фермы, известно, то следует принимать известное значение расчетного сопротивления, если расчетное сопротивление не известно, то лучше принимать значение, минимальное из возможных, как в данном случае.

Так как у нас имеется более чем двукратный запас по прочности рассчитывать стержень б-в нет большой необходимости. Ну а дальше количество вариантов конструирования поистине безгранично. Например, можно уменьшить сечение профильной трубы, это приведет к увеличению значения коэффициента гибкости, например, для профильной трубы сечением 25х25х1.5 мм площадью сечения 1.37 см² i = 0.951 см, λ = 106.4, φ = 0.516 и тогда

1269.34/(0.516·1.37) = 1795.68 кгс/см² < R_y = 2350 кгс/см²;

Однако чем тоньше стенки трубы, тем труднее их аккуратно сварить. А вот если использовать более крупное сечение, то можно сделать не 6, а 4 или даже 3 фермы, а это экономия по времени работы в 1.5-2 раза. Для изготовления 4 ферм с шагом 1.67 м и даже 3 ферм с шагом 2.5 м вполне можно использовать профильную трубу сечением 30х30х2 мм, при таком шаге только увеличится значение продольной силы:

1269.34·2.5/(0.625·2.17) = 2339.8 кгс/см² < R_y = 2350 кгс/см²;

Проверим устойчивость стержня б-в для данного сечения. Так как расчетная длина стержня б-в меньше, то соответственно будет меньше и значение λ = 59.3/1.133= 52.3, тогда φ ≈ 0.84

1527.34·2.5/(0.83·2.17) = 2120 кгс/см² < R_y = 2350 кгс/см²;

Таким образом все необходимые условия по прочности и устойчивости нами соблюдены. Однако если учесть, что в стержнях фермы будут возникать дополнительные напряжения, например, при неравномерном проседании колонн фундамента, что вполне вероятно, то лучше не рисковать, а подбирать сечение с хорошим запасом.

Примечание: При уменьшении количества ферм пролет балок обрешетки значительно увеличивается и значит для балок обрешетки придется использовать профильные трубы большего сечения. Но это и есть тонкости проектирования и поиска оптимального варианта.

А вот если нет возможности расположить опоры фермы так, как показано на рисунке 272.1, а только по концам фермы, то в этом случае ферма будет бесконсольной и нагрузки в стержнях фермы при сохранении геометрии фермы будут совсем другие и тогда усилия во всех стержнях следует просчитывать. Для примера, наибольшее сжимающее усилие будет возникать в стержне N_2-а. Из-за перемещения опорной реакции V_A из точки 3 в точку 1 и уравнение моментов относительно все той же точки 3 будет иметь следующий вид (сечение I-I):

М₃ = -1.5Q/2 + 1.5V_A + 1.5N_2-asinα = 0;

N_2-а = (0.5Q - 5Q)/sinα = - 4.5·190/0.158 = - 5411.88 кг

В данном случае стержень 2-а будет работать на сжатие и усилия в этом стержне будут в 4.2 раза больше, чем при расчетной схеме фермы с консолями и для таких ферм (как минимум четырех) сразу потребуется профильная труба сечением 40х40х2.5 мм. Уменьшение высоты фермы также приведет к увеличению напряжений в стержнях фермы, да и стыки профнастила при уменьшении уклона уже не будут так надежно защищать от атмосферных осадков.

Таковы вкратце основные принципы расчета и проектирования треугольных ферм.

P.S. Я прекрасно понимаю, что человеку, впервые столкнувшемуся с расчетом строительных конструкций, разобраться в тонкостях и особенностях вышеизложенного материала бывает не просто, но тратить тысячи или даже десятки тысяч рублей на услуги проектной организации вы все равно не хотите. Что ж, я готов помочь вам в расчете, но только после того, как вы поможете проекту (соответствующая форма размещена после комментариев). Больше подробностей смотрите в статье "Записаться на прием к доктору".

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

На главную

• Расчет конструкций ::: Расчет металлоконструкций
• Расчет конструкций ::: Основы строймеха и сопромата ::: Фермы

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).