Например, в "Пособии по проектированию бетонных и ж/б конструкций из тяжелого бетона... (к СП 52-101-2003)" приводится расчет на прогиб железобетонной прямоугольной плиты перекрытия - шарнирно опертой бесконсольной балки размерами h = 20 см, b = 100 см; ho = 17.3 см; пролетом l = 5,6 м; бетон класса В15 (Еb = 245000 кгс/см2, Rb = 85 кгс/см2); растянутая арматура класса А400 (Es= 2·106 кгс/см2) с площадью поперечного сечения As = 7.69 cм2 (5 Ø14); полная равномерно распределенная нагрузка q = 7,0 кН/м. В результате расчета прогиб такой плиты составляет f = 3.15 см, что больше максимально допустимого. Значение максимально допустимого прогиба определяется согласно СНиП 2.01.07-85 "Нагрузки и воздействия". Так для плиты перекрытия в жилом доме длиной 5.6 м, если под ней нет перегородок, максимально допустимый прогиб составляет fu = l/200 = 560/200 = 2.8 см.
Между тем, если рассчитать эту же плиту на прочность согласно требований того же СП 52-101-2003, то требуемая площадь арматуры (согласно формул 3.2 и 3.3 указанного СП) составит Аs = 4.67 см2, т.е. почти в 1.6 раза меньше.
Как же быть в этом случае? Неужели и дальше штурмовать обледенелые вершины знаний, накопленных в соответствующих нормативных документах, или есть все-таки более простая и короткая дорога к цели? На мой взгляд есть, но это всего лишь мое личное мнение.
Приводимый ниже расчет не совсем соответствует рекомендациям СНиП 2.03.01-84 и СП 52-101-2003, тем не менее позволяет приблизительно определить значение прогиба по упрощенной методике. И хотя шарнирно опертая безконсольная однопролетная балка c прямоугольной формой поперечного сечения, на которую действует равномерно распределенная нагрузка - это частный случай на фоне множества возможных видов нагрузок, расчетных схем и геометрических форм сечения, тем не менее это очень распространенный частный случай в малоэтажном строительстве.
Пример расчета деформации железобетонной плиты, как балки переменного сечения
Прогиб плиты при выбранной расчетной схеме составит
f = k5ql4/384EIp (321.1)
Как видим, формула достаточно проста и отличается от классической наличием дополнительного коэффициента. Коэффициент k учитывает изменение высоты сжатой области сечения по длине балки при действии изгибающего момента. При равномерно распределенной нагрузке и работе бетона в области упругих деформаций значение коэффициента для приближенных расчетов можно принимать k = 0.86. Использование этого коэффициента позволяет определять прогиб балки (плиты) переменного сечения, как для балки постоянного сечения с высотой hmin. Таким образом в приведенной формуле остается только 2 неизвестных величины - расчетное значение модуля упругости бетона и момент инерции приведенного сечения Ip в том месте, где высота сечения минимальна. Остается только определить этот самый момент инерции, а модуль упругости примем равный начальному.
Для наглядности дальнейший расчет будет произведен для упоминавшейся выше плиты.
Теоретические предпосылки и допущения, принимаемые при определении прогиба ж/б плиты, работающей в области упругих деформаций
1. Так как соотношение длины плиты к высоте l/h = 560/20 = 28, т.е. значительно больше 10, то влияние поперечных сил на прогиб можно не учитывать.
2. Балка (плита) состоит из материалов, имеющих различные модули упругости, поэтому нейтральная линия - ось балки будет проходить не через центры тяжести поперечных сечений, а будет смещена и будет проходить через приведенные центры тяжести. Положение приведенных центров тяжести будет зависеть от соотношения модулей упругости бетона и арматуры.
3. Так как модуль упругости стали значительно больше начального модуля упругости бетона, то при рассмотрении геометрических параметров поперечного сечения плиты, как некоего единого сечения, площадь сечения арматуры следует умножить на отношение Еs/Eb. Для плиты это соотношение составит as1 = 2000000/245000 = 8.163
Определение момента инерции приведенного сечения
4. На приопорном участке плиты из-за малого значения внутренних нормальных напряжений на растяжение будет работать вся нижняя часть сечения, т.е. и бетон и арматура. Так как момент инерции условно сжатого сечения (материал - бетон), должен быть равен моменту инерции условно растянутого сечения (материалы бетон и арматура), то при прямоугольной форме поперечного сечения (постоянном значении ширины b по всей высоте сечения), моменты инерции для условно сжатого и условно растянутого сечения относительно приведенной нейтральной оси составят:
Iс = Wcy = 2by3/3 = b(2y)3/12 = Iр = 2b(h - y)3/3 + 2As(ho - y)2Es/Eb (321.2.1)
из чего можно вывести следующее кубическое уравнение:
у3 = (h - y)3 + 3As(ho - y)2Es/bEb (321.2.2)
Примечание: собственный момент инерции для стержней арматуры в виду малого его значения для упрощения расчетов мы не учитываем.
Решение этого уравнения для рассматриваемой плиты даст следующий результат уо = 10.16 см, что в принципе логично при общей высоте балки h = 20 см. В принципе, для приближенных расчетов значение высоты сжатой зоны на участках без трещин можно вообще не определять, так как при предлагаемом методе расчета значение высоты сжатой зоны на участках без трещин нужно только для оценки изменения высоты сечения по длине балки (на основании этого изменения и принимается значение коэффициента k)
5. Посредине плиты, где в результате действия максимальных нормальных напряжений трещины будут максимальными, на растяжение будет работать только арматура, работой бетона из-за малой высоты растянутой зоны сечения бетона можно пренебречь. При разнице сопротивлений бетона сжатию и растяжению в 10 раз, разница высот сжатой и растянутой зоны бетона в результате образования трещин также будет составлять 10 раз. При этом разница в моментах инерции для таких частей сечения будет составлять 103 раз.
6. Моменты инерции для частей сечения посредине плиты составят:
Iс = Wcy = 2by3/3 = Iр = 2As(ho - y)2Es/Eb (321.2.3)
из чего можно вывести следующее кубическое уравнение:
у3 = 3As(ho - y)2Es/bEb (321.2.4)
Решение этого уравнения для рассматриваемой плиты даст следующий результат уl/2 = 6.16 см.
Примечание: Иногда, если значение у с точностью до сотых долей миллиметра вас не интересует, а решение кубических уравнений вызывает определенные проблемы, то можно подобрать приближенное значение у за 2-5 минут, подставляя то или иное значение в уравнение (321.2.4) и смотря на результаты правой и левой части.
7. Использование этого значения высоты сжатой зоны для дальнейших расчетов будет корректным при работе бетона в области упругих деформаций (рис. 321.а). Если в сжатой зоне в результате деформаций будет происходить перераспределение напряжений (рис.321.1.б), то высоту сжатой зоны при данной методике расчета следует уменьшить:
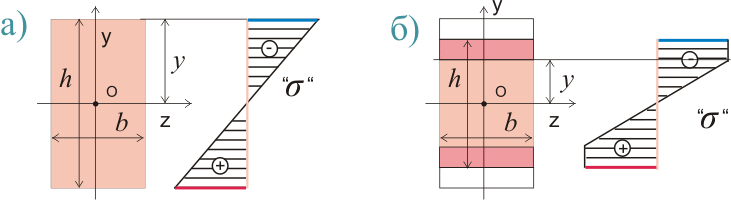
Рисунок 321.1
8. Определим высоту сечения, минимально допустимую расчетами на прочность без учета пластических деформаций.
Так как расчет прочности может производиться из условия
M/W ≤ Rb; W ≥ M/Rb = ql2/8Rb = 7·5602/(8·85) = 3228.23 см3 (321.3.1)
W = 2by22/3 (222.1.5.1)
то деформации в сжатой зоне бетона будут упругими при
y2 = (3W/2b)1/2 = (3·3228.23/200)1/2 = 6.96 см (321.3.2)
9. Так как высота сжатой зоны бетона в процессе деформации будет меньше высоты, необходимой для линейно изменяющегося распределения нормальных напряжений по высоте (разница показана на рисунке 321.1.б белым прямоугольником) , то это приведет к перераспределению нормальных напряжений (подобное перераспределение показано на рисунке 321.б) достаточно условно). В итоге площадь эпюр в обоих случаях будет одинаковой (так как значение изгибающего момента не меняется), а высота зоны упругих деформаций еще уменьшится на у2 - у. Таким образом расчетное значение высоты приведенного сечения составит:
hmin = ур = у - (у2 - у) = 6.16 - (6.96 - 6.16) = 5.36 см (321.4)
10. Расчетный момент инерции составит
Ipасч = 2byp3/3 = 2·100·5.363/3 = 10266 см4 (321.5)
11. Значение прогиба при полной нагрузке составит
f = 0.86·5·7·5604/(384·245000·10266) = 3.065 см (321.6)
12. Требование СНиП 2.01.07-85:
f = 3.065 см ≤ fu = 2.8 см (321.7)
не соблюдено. А это означает, что для соблюдения требований нужно или увеличивать класс бетона, или увеличивать сечение арматуры, или увеличивать высоту сечения. Впрочем, все это прямого отношения к расчету на прогиб не имеет.
Примечание: Один из недостатков приведенного выше способа определения прогиба состоит в в том, что при расчетах мы не учли возможное изменение модуля упругости при длительном действии нагрузки и различных других факторах. Нельзя сказать, что более точный учет модуля упругости внесет страшное смятение в стройные ряды прогиба, тем не менее, расчет с учетом уточненного значения модуля упругости будет более точным. | 
