Расчет балок равного сопротивления изгибающему моменту

Расчет на прочность балок равного сопротивления изгибающему моменту, другими словами балок, нормальные напряжения в поперечных сечениях которых постоянны, мало чем отличается от расчета балок постоянного сечения, так как требования по прочности остаются неизменными - напряжения в максимально нагруженном сечении не должны превышать максимально допустимых. А вот определение деформаций балок равного сопротивления изгибающему моменту имеет свои особенности.

Теоретические предпосылки и допущения, принимаемые при расчете балок переменного сечения

1. Расчет допускается выполнять на основе теоретических предпосылок и допущений, принимаемых при формулировке задач теории сопротивления материалов.

2. Так как значения изгибающих моментов, продольных и поперечных сил не зависят от геометрических характеристик рассматриваемого сечения, то эти значения при расчетах балок переменного сечения принимаются такими же, как и для балок постоянного сечения.

3. В качестве балок переменного сечения могут рассматриваться только такие тела, изменение геометрических параметров сечения которых не влияет на положение нейтральной оси, или соотношение длины балки к изменению высоты по длине больше 50: l/Δh ≥ 50, так как в этом случае влияние горизонтальных опорных реакций, возникающих из-за непрямолинейности нейтральной оси балки, можно не учитывать.

4. При изменении ширины сечения по длине следует учитывать особенности приложения нагрузки. Для элементов конструкции, к которым приложена сосредоточенная нагрузка в месте наибольшей ширины, следует учитывать местную концентрацию напряжений в месте приложения сосредоточенной нагрузки. Если 50 > l/Δh > 10, то такой элемент можно рассматривать как стержень переменного сечения малой кривизны (большого радиуса кривизны). При l/Δh < 10 элемент рассматривается как стержень переменного сечения большой кривизны (малого радиуса кривизны), или как арка переменного сечения.

5. При расчете балок ступенчатого сечения с прямолинейной нейтральной осью (валов машин и механизмов) концентрации напряжений, возникающие в местах резкого изменения геометрических параметров сечения, учитываются соответствующими коэффициентами, расчет таких балок в данной статье не рассматривается.

6. При незначительном изменении геометрических параметров по отношению к длине влияние перераспределения нормальных и касательных напряжений можно не учитывать, принимая влияние этих изменений в пределах погрешности. Это обеспечивается использованием соответствующего коэффициента надежности.

7. Обычно при расчетах на прочность элементов конструкций, работающих на изгиб, сначала определяется значение максимального изгибающего момента, а затем в зависимости от значения момента сопротивления и расчетного сопротивления материала подбираются геометрические параметры сечения, исходя из следующего условия:

σ_max = M_max/W_z ≤ R ↔ W_z ≥ M/R (320.1.1)

где σ_max - максимальные нормальные напряжения, возникающие в рассматриваемом поперечном сечении, R - расчетное сопротивление материала, W_z - момент сопротивления материала относительно оси z:

W_z = 2I_z/h (320.1.2.1)

для прямоугольного сечения

W_z = bh²/6 (320.1.2.2)

Для расчетов на прочность элементов постоянного сечения и даже элементов переменного сечения этого вполне достаточно, так как для соблюдения прочности необходимо, чтобы материал выдерживал возникающие в наиболее нагруженном поперечном сечении напряжения. Между тем углы поворота поперечных сечений и прогибы - вертикальные смещения поперечных сечений - результат действия напряжений по всей длине элемента. Поэтому при определении углов поворота и прогибов необходимо учитывать изменение параметров поперечного сечения по длине элемента.

При несимметричных нагрузках, при несимметрично изменяющихся параметрах сечения, при непрямоугольных поперечных сечениях и при расчете многопролетных статически неопределимых балок следует использовать методы дифференциального исчисления, позволяющие учесть указанные особенности.

Если изменения геометрических параметров и действующие нагрузки симметричны относительно оси проходящей через середину пролета, то для балок прямоугольного сечения сделать это можно следующим образом:

8. 1. Если эпюра изменения одного из параметров описывается той же зависимостью, что и эпюра моментов, то такую балку можно рассматривать, как балку пропорционального сопротивления, а если при выбранных параметрах сечения напряжения остаются постоянными, то такая балка называется балкой равного сопротивления изгибающему моменту. Балка, изменение ширины которой показано на рис. 320.1.в), при приложении сосредоточенной нагрузки посредине балки (рис. 320.1.а) будет балкой равного сопротивления изгибающему моменту. При этом эпюра моментов будет обычной, а эпюра нормальных напряжений для такой балки также будет иметь вид прямоугольника (рис. 320.3.г):

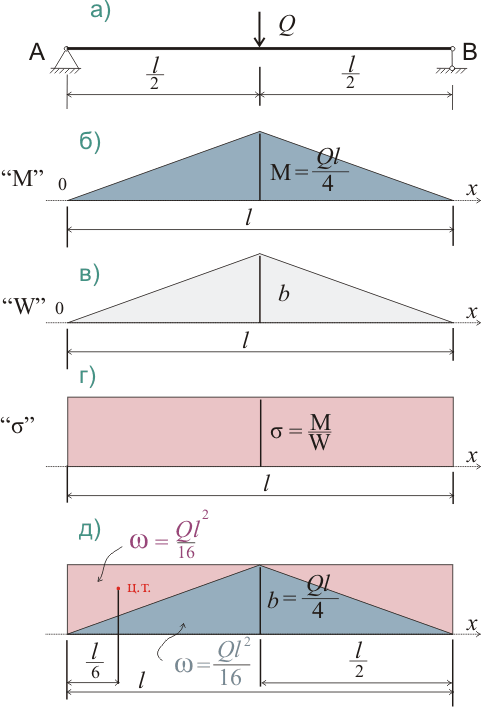
Рисунок 320.1

8.2. Если эпюру моментов наложить на эпюру нормальных напряжений, то разница эпюр покажет изменение прогиба балки.

Для того, чтобы корректно наложить эпюры, воспользуемся следующим допущением. Если значение напряжений в середине пролета рассматривать как некое единичное (σ_l/2 = 1) и при постоянной высоте сечения h значение h²/6 заменить постоянной С, также равной единице (С = 1), то тогда согласно формул (320.1.1) и (320.2.2):

1 = М/bC = М/b (320.3.1)

тогда

b = M = Ql/4 (320.3.2)

8.3. Прогиб балки постоянного сечения можно определить по эпюре моментов и напряжений графо-аналитическим методом.

Вкратце суть графоаналитического метода состоит в том, что эпюра изгибающего момента рассматривается как некая фиктивная нагрузка. Соответственно, чтобы определить фиктивную опорную реакцию от такой нагрузки, нужно определить площадь эпюры (это будет угол поворота на опоре А), а чтобы определить значение фиктивного изгибающего момента, нужно сначала умножить значение фиктивной опорной реакции на расстояние до рассматриваемой точки и затем вычесть из этого значения площадь эпюры фиктивной нагрузки, умноженную на расстояние от центра тяжести фиктивной нагрузки до рассматриваемой точки (это будет прогиб посредине пролета).

8.4. Тогда если площадь фигуры, показывающей разницу между эпюрой моментов и эпюрой напряжений, умножить на расстояние от центра тяжести этой фигуры до середины пролета, то полученный фиктивный момент будет показывать разницу между прогибом балки постоянного сечения и прогибом балки изменяющегося сечения при той же нагрузке.

Для балки, показанной на рисунке 320.1 дополнительный прогиб, вызванный равномерным распределением напряжений по всей длине балки, составит:

M_ф= Ql²/16(l/2) - Ql²/16(l/6) = Ql³/96;  f_σ = Ql³/96EI_b (320.4.1)

В данной случае I_b означает, что мы рассматриваем изменение прогиба по отношению к балке с постоянным моментом инерции и соответственно постоянной шириной сечения b.

Общий прогиб балки равного сопротивления изгибающему моменту составит:

f_об = f_п + f_σ = Ql³/48EI_b + Ql³/96EI_b = Ql³/32EI_b (320.4.2)

Балка равного сопротивления изгибающему моменту при действии равномерно распределенной нагрузки по всей длине балки будет иметь другие параметры поперечного сечения, однако принцип расчета остается таким же:

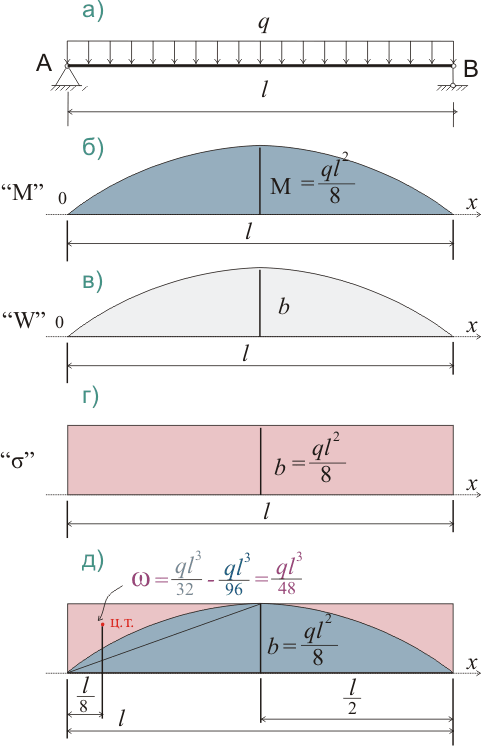
Рисунок 320.2

Для балки с равномерно распределенной нагрузкой:

M_ф =ql³/48(l/2) - ql³/48(3l/8) = ql³/384;  f_σ = ql⁴/384EI_b (320.5.1)

Тогда прогиб балки равного сопротивления изгибающему моменту составит:

f_об = f_п + f_σ = 5ql⁴/384EI_b + ql⁴/384EI_b = ql⁴/64EI_b (320.5.2)

А если балка имеет не равное сопротивление изгибающему моменту, например, ширина сечения балки изменяется линейно (рис.320.1.в), то следует учесть дополнительный прогиб, возникающий из-за неравномерного распределения напряжений:

M^σ_ф = ql³/96(l/4) = ql³/384;  f^σ = ql⁴/384EI_b (320.5.3)

Тогда общий прогиб балки не равного сопротивления изгибающему моменту составит:

f_об = f_п + f_σ + f^σ = 5ql⁴/384EI_b + ql⁴/384EI_b + ql4/384EI_b = 7ql⁴/384EI_b (320.5.4)

Примечание: Принципы определения площадей фигур, описанных различными кривыми и определения центра тяжести таких фигур в данной статье не рассматриваются.

Важно: При расчетах на прочность балок не равного сопротивления моменту следует рассматривать сечение, в котором возникают наибольшие напряжения. В данном случае сечение, расположенное на расстоянии 0.25l от начала пролета. Одним из вариантов увеличения прочности будет увеличение ширины балки на некоторую постоянную величину b_min. Тогда такую балку можно рассматривать как две: одну балку постоянного сечения с шириной b_min и вторую с шириной, изменяющейся от 0 до Δb = b_max - b_min.

9. Расчет балок равного сопротивления изгибающему моменту с изменяющейся высотой отличается только тем, что согласно формулы (320.1.2.2) высота сечения будет выражаться квадратным корнем из изгибающего момента.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

На главную

• Расчет конструкций ::: Основы строймеха и сопромата ::: Балки

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).