Итак, рассмотрим следующую ситуацию. Проектируется перекрытие по деревянным балкам. Вот только имеющегося в распоряжении лесоматериала - балок сечением 5х15 см - для обеспечения необходимой прочности не хватает.
Момент сопротивления таких балок составляет Wz = bh2/6 = 5·152/6 = 187.5 cм3, при пролете 4 м, шаге балок 0.5 м и расчетной плоской нагрузке 400 кг/м2 максимальный изгибающий момент составляет М = ql2/8 = 200·42/8 = 400 кгм или 40000 кгсм, а при расчетном сопротивлении древесины R = 140 кг/см2 требуемый момент сопротивления составит Wтр = М/R = 4000/140 = 285.7 см3, т.е. в 1.5 раза больше фактического.
Потому деревянные балки (момент инерции такой балки составляет I = 5·153/12 = 1406.25 см4) решено усилить металлической полосой снизу сечением 5х1 см. Момент инерции такой полосы сам по себе составляет I = 5·13/12 = 0.417 см4, т.е. момент инерции стальной полосы настолько мал, что им вроде бы для упрощения расчетов можно пренебречь. Но не будем спешить, потому как даже если эта полоса была бы деревянной, то все равно общий момент инерции балки при этом увеличился бы до I = 5·163/12 = 1706 cм4.
Как мы знаем, несущая способность балки зависит от момента сопротивления поперечного сечения, а величина деформации (прогиба) - от момента инерции того же поперечного сечения. Вот только в данном случае у нас получается поперечное сечение балки из разных материалов и у этих материалов различные модули упругости. Как тут быть?
Ответ прост: нужно привести фактически имеющееся сечение из материалов с разными модулями упругости к некоему условному сечению, имеющему один модуль упругости. Такое сечение называется приведенным.
В данном случае модуль упругости стали составляет около Ес = 2·106 кг/см2, а модуль упругости древесины - Ед = 105 кг/см2. Т.е. модуль упругости стали в 20 раз больше. Из этого следует, что момент инерции той части приведенного сечения, которая заменяет металлическую полосу, будет в 20 раз больше, т.е. коэффициент приведения n = Ec/Eд = 20.
Как правило дальнейший расчет производится, исходя из следующих соображений:
1. Общая высота приведенного сечения остается такой же, как и у фактического сечения. Т.е. увеличение момента инерции в 20 раз означает и увеличение площади приведенной части сечения в 20 раз.
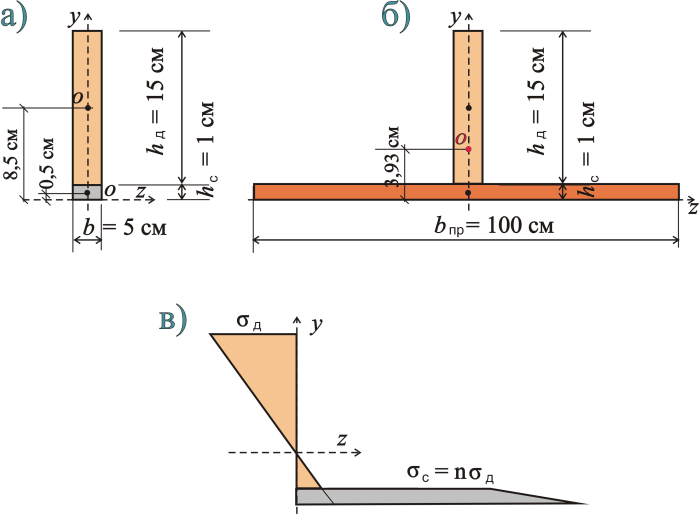
Рисунок 461.1. а) геометрические параметры реального сечения, б) приведенного сечения, в) нормальные напряжения в сечении
2. Тогда площадь приведенного сечения составит:
Fпр = Fд + nFс = 5х15 + 20(5х1) = 75 + 100 = 175 см2.
3. После этого определяется координата центра тяжести приведенного сечения, необходимая для определения момента инерции приведенного сечения.
Определить координаты центра тяжести для приведенного сечения мы можем, воспользовавшись знаниями о статическом моменте сечения. Так расстояние от оси z, проходящей через низ сечения металлической полосы, до центра тяжести приведенного сечения составит:
ус =(Sд + nSс)/Fпр = (75·8.5 + 20·5·0.5)/175 = 3.93 см
Примечание: если бы объемный вес металла был в 20 раз больше объемного веса древесины, то определенный таким образом центр тяжести совпадал бы с фактическим центром тяжести для данного сечения. Однако нас в данном случае интересует не фактический центр тяжести, а некая точка, через которую проходит нейтральная ось балки, поэтому в данном случае понятие "центр тяжести" не следует понимать буквально.
Кроме того, рассматриваемая ось у может проходить через центр тяжести стальной пластины (т.е. на 0.5 см выше) и в этом случае расчеты упростятся, так как статический момент для стальной пластины в этом случае будет равен нулю и тогда
ус = Sд/Fпр = 75·8/175 = 3.43 см
4. Момент инерции рассматриваемого приведенного сечения составит:
Izпр = Izд + nIzc = (1406.25 + 75(8.5 - 3.93)2) + 20(0.417 + 5(3.93 - 0.5)2) = 1406.25 + 1566.3675 + 1184.83 = 4157.45 см4.
5. Максимальные нормальные напряжения в рассматриваемом приведенном сечении составят:
σд = Му/Iпр = 40000(16 - 3.93)/4157.45 = 116.13 кг/см2 < Rд = 140 кг/см2
σс = nMy/Iпр = 20·40000·3.93/4157.45 = 756 кг/см2 < Rc = 2100 кг/см2
В данном случае у - это расстояние от центра тяжести приведенного сечения до верхней точки (древесина) и нижней точки (сталь) сечения.
Так как площадь фактического сечения стальной полосы в 20 раз меньше, то соответственно значение нормальных напряжений умножается на коэффициент приведения.
6. Максимальный прогиб для балки из разнородных материалов составит
f = 5ql4/384EIпр = 5·4·4004/384·105·4157.45 = 3.2 см > fдоп = l/200 = 400/200 = 2 см.
В данном случае при расчетах используется модуль упругости древесины. Впрочем можно было бы использовать и модуль упругости стали, но при этом знаменатель дополнительно умножить на коэффициент приведения.
Как видим, не смотря на то, что максимальные нормальные напряжения не превышают расчетных сопротивлений, тем не менее прогиб все равно будет больше допустимого. Это означает, что такого усиления деревянной балки для обеспечения необходимой жесткости не достаточно.
Теоретически можно увеличить ширину стальной полосы, однако при этом разница напряжений в области сопряжения дерева и стали еще более увеличится, а центр тяжести приведенного сечения еще более сместится к стальной пластине, что приведет к относительно незначительному увеличению приведенного момента инерции. Потому более эффективным будет все-таки увеличить высоту сечения деревянной балки и потом уже усиливать ее металлом. Да и по рисунку 461.1 это видно невооруженным глазом (но мозги при этом должны быть достаточно вооружены знаниями теории сопротивления материалов).
Например, при использовании деревянных балок сечением 5х20 см и той же стальной полосе 5х1 см:
Fпр = 100 + 100 = 200 см2
ус = (100·11 + 50)/200 = 5.75 см
Izпр = 5·203/12 + 100(11 - 5.75)2 + 20(0.417 + 5(5.75 - 0.5)2) = 3333.33 + 2756.25 + 2764.59 = 8854.17 см4
Так как приведенный момент инерции увеличился в 8854.17/4157.45 = 2.13 раза, то соответственно и прогиб балки уменьшится в 2.13 раза и составит
f = 3.2/2.13 = 1.5 см.
Вот собственно и весь расчет. | 
