Основы сопромата, расчет прогиба балки - Доктор Лом

На главную
Поиск по сайту Что это за доктор? Записаться на прием

Основы сопромата, расчет прогиба балки
Часто при расчете строительных конструкций важно определить не только геометрические параметры сечения конструкции, но и величину прогиба конструкции с точностью до миллиметра. Дело в том, что величина прогиба для любой конструкции нормируется различными СНиПами и не должна превышать 1/250 для балок междуэтажных перекрытий, 1/200 для чердачных перекрытий и перемычек и так далее, список длинный. Когда расчет производится для себя (например строится частный дом и нужно сделать балки перекрытия или перемычки), то определять величину прогиба не обязательно, никто Вас ругать не будет, главное чтобы по несущей способности расчет был верный, но все же определить прогиб конструкции желательно. Ведь знание величины прогиба позволить более точно выбрать, например, вариант отделки потолка.

Cодержание: Основы сопромата кратко. 1. Виды опор. 1.1. Шарнирные опоры. Расчетная длина (пролет) балки. 1.2. Опорные связи шарнирно закрепленной балки. 1.3 Жесткое защемление на опорах. 1.4. Скользящие заделки. 2. Нагрузки (внешние силы). 3. Напряжения (внутренние силы). 4. Реакции опор. 5. Уравнения статического равновесия. 4.1. Определение опорных реакций. 6. Уравнения изгибающего момента. 7. Балка на двух шарнирных опорах. 8. Консольная балка. 9. Метод сечений. 10. Определение момента сопротивления. 11. Определение угла поворота. 12. Определение прогиба. 13. Определение угла поворота через прогиб. 14. Список использованной литературы. Расчет прогиба балки не то, чтобы такой уж сложный, но для того, чтобы каждый раз не повторять одни и те же операции при расчете и этим максимально сократить время расчета, специалисты по сопромату уже давно вывели формулы для наиболее вероятных вариантов опор балок и нагрузок, действующих на балки. Достаточно только определиться с расчетной моделью балки и *формула для расчета прогиба* к Вашим услугам. Но аксиомы: "если хочешь, чтобы работа была сделана хорошо, сделай это сам" пока никто не отменял. Дело в том, что в разного рода справочниках и пособиях иногда бывают опечатки или ошибки, поэтому использовать готовые формулы не всегда есть хорошо. 11. Определение угла поворота. (вернуться к основному содержанию) Прогиб строительной конструкции, а в нашем случае балки - единственная величина, которую проще всего определить опытным путем и сложнее всего теоретическим. 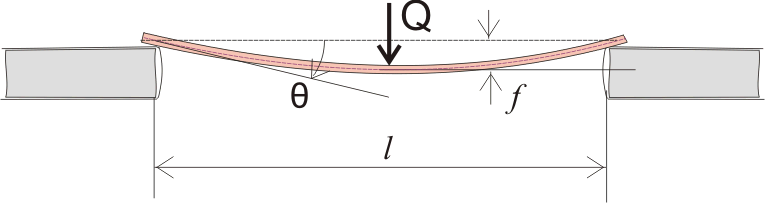Когда мы прикладывали к линейке нагрузку (давили на нее пальцем или мощью своего интеллекта), то невооруженным глазом видели, что линейка прогибалась: Рисунок 11.1. Перемещение центра тяжести поперечного сечения балки в центре балки и угол поворота продольной оси, проходящей через центр тяжести поперечного сечения, на одной из опор. Если бы мы хотели определить величину прогиба опытным путем, то достаточно было бы измерить расстояние от стола, на котором лежат книги (на рисунке не показан) до верха или низа линейки, затем приложить нагрузку и измерить расстояние от стола до верха или низа линейки. Разница в расстояниях - это и есть искомый прогиб (на фотографии величина прогиба обозначена оранжевой линией): Фотография 1. Но попробуем прийти к тому же результату, следуя по тернистому пути теории сопромата. Так как балка прогнулась (в хорошем значении этого слова), получается, что и продольная ось, проходящая через центры тяжести поперечных сечений всех точек балки, и до приложения нагрузки совпадавшая с осью х, сместилась. Это смещение центра тяжести поперечного сечения по оси у называется прогибом балки f. Кроме того, очевидно, что на опоре эта самая продольная ось теперь находится под некоторым углом θ к оси х, а в точке действия сосредоточенной нагрузки угол поворота = 0, так как нагрузка у нас приложена посредине и балка прогнулась симметрично. Угол поворота принято обозначать "θ", а прогиб "f" (во многих справочниках по сопромату прогиб обозначается как "ν", "w" или любыми другими литерами, но нам, как практикам, удобнее использовать обозначение "f", принятое в СНиПах). Как определить этот самый прогиб мы пока не знаем, но зато мы знаем, что нагрузка, действуя на балку, создает изгибающий момент. А изгибающий момент создает внутренние нормальные сжимающие и растягивающие напряжения в поперечных сечениях балки. Эти самые внутренние напряжения приводят к тому, что в верхней части балка сжимается, а в нижней растягивается, при этом длина балки по оси, проходящей через центры тяжести поперечных сечений остается такой же, в верхней части длина балки уменьшается, а в нижней части увеличивается, причем чем дальше расположены точки поперечных сечений от продольной оси, тем больше будет деформация. Определить эту самую деформацию мы можем используя еще одну характеристику материала - модуль упругости. Если мы возьмем кусок бинтовой резины и попробуем его растянуть, то обнаружим, что резина растягивается очень легко, а выражаясь по научному деформируется на значительную величину при воздействии даже небольшой нагрузки. Если мы попробуем проделать то же самое с нашей линейкой, то растянуть ее даже на десятые доли миллиметра руками вряд ли получится, даже если прилагать к линейке нагрузку в десятки раз большую, чем к бинтовой резине. Это свойство любого материала описывается модулем Юнга, который часто называется просто модулем упругости. Физический смысл модуля Юнга при максимально допустимом загружении рассчитываемой конструкции примерно следующий: модуль Юнга показывает отношение нормальных напряжений, (которые при максимально допустимом загружении равны расчетному сопротивлению материала к относительной деформации при таком загружении: E = R/Δ (11.1.1) а это значит, что для работы материала в области упругих деформаций значение внутренних нормальных напряжений, действующих не абстрактно, а на вполне определенную площадь сечения, с учетом относительной деформации не должно превышать значения модуля упругости: E ≥ N/ΔS (11.1.2) в нашем случае балка имеет прямоугольное сечение, поэтому S = b·h, где b - ширина балки, h - высота балки. Измеряется модуль Юнга в Паскалях или кгс/м². Для абсолютного большинства строительных материалов модули упругости определены эмпирическим путем, узнать значение модуля для того или иного материала можно по справочнику или сводной таблице. Определить величину деформации для поперечного сечения, к которому приложена равномерно распределенная нагрузка или сосредоточенная сила в центре тяжести поперечного сечения, очень просто. 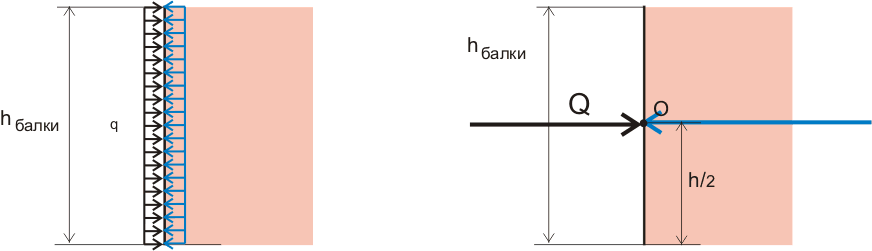В таком сечении возникают нормальные сжимающие или растягивающие напряжения, равные по значению действующей силе, направленные противоположно и постоянные по всей высоте балки (согласно одной из аксиом теоретической механики): Рисунок 507.10.1 и тогда определить относительную деформацию, если известны геометрические параметры балки (длина, ширина и высота) несложно, простейшие математические преобразования формулы (11.1.2) дают следующий результат: Δ = Q/(S·Е) (11.2.1) или Δ = q·h/(S·Е) (11.2.2) Так как расчетное сопротивление показывает какую максимальную нагрузку можно приложить к определенной площади, то в данном случае мы можем рассматривать действие сосредоточенной нагрузки на всю площадь сечения нашей конструкции. В некоторых случаях важно определить деформации именно в точке приложения сосредоточенной нагрузки, но сейчас мы эти случаи не рассматриваем. 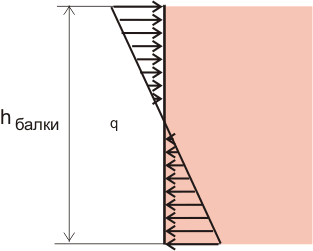Чтобы определить суммарную деформацию, нужно обе части уравнения умножить на длину балки: Δl = Q·l/(b·h·Е) (11.2.3) или Δl = q·h·l/(b·h·Е) (11.2.4) Но в рассматриваемом нами случае на поперечные сечения балки действует не сосредоточенная сила, приложенная к центру тяжести поперечного сечения, а изгибающий момент, который можно представить в виде следующей нагрузки: Рисунок 149.8.3 При такой нагрузке максимальные внутренние напряжения и соответственно максимальные деформации будут происходить в самой верхней и в самой нижней части балки, а посредине никаких деформаций не будет. Равнодействующую для такой распределенной нагрузки и плечо действия сосредоточенной силы мы находили в предыдущей части (2), когда определяли момент сопротивления балки. Поэтому теперь без особого труда можем определить суммарную деформацию в самой верхней и в самой нижней части балки: Δх = M·х/((h/3)·b·(h/2)·Е) (11.3.1) или Δх = M·х/(W·Е) (11.3.2) так как W = b·h²/6 (10.6) Эту же формулу мы можем получить и другим способом. Как мы знаем, момент сопротивления поперечного сечения балки должен удовлетворять следующему условию: W ≥ М / R (10.3) Если мы будем рассматривать эту зависимость как уравнение и заменим в этом уравнении значение R на ΔЕ, получим следующее уравнение: W = М / ΔЕ (11.4.1) И тогда: М = WΔЕ (11.4.2) a Δ = M/(W·Е) (11.4.5) и соответственно Δх = M·х/(W·Е) (11.3.2) В результате деформации, которую мы только что определили, наша балка могла была бы выглядеть так: 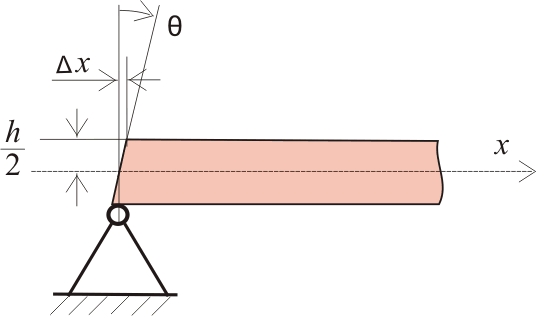Рисунок 11.2. Предполагаемая (для наглядности) деформация балки то есть в результате деформаций самая верхняя и самая нижняя точки поперечного сечения сместятся на величину Δх. А это значит, что зная величину деформации и высоту балки, мы можем определить угол поворота θ поперечного сечения на опоре балки. Из школьного курса геометрии мы знаем, что отношение катетов прямоугольного треугольника (в нашем случае катеты Δх и h/2) равно тангенсу угла θ: tgφ = Δх/(h/2) (11.5.1) и тогда tgφ = 2 M·х/(h·W·Е) (11.5.3) Если вспомнить, что момент инерции - это момент сопротивления поперечного сечения, умноженный на расстояние от центра тяжести до крайней точки сечения или наоборот, момент сопротивления - это момент инерции, разделенный на расстояние от центра тяжести до крайней точки сечения: W = I/(h/2) (10.7) или I = W·h/2 (10.7.2) то мы можем заменить момент сопротивления на момент инерции: tgφ = M·х/(I·Е) (11.5.4) хотя делать это было не обязательно, но таким образом мы получили формулу угла поворота почти такой, как она дается во всех учебниках и справочниках по сопромату. Главное отличие в том, что обычно речь идет о угле поворота, а не о тангенсе угла. И хотя при малых деформациях значения тангенса угла и угол сопоставимы, но тем не менее угол и тангенс угла - это разные вещи (впрочем в некоторых справочниках, например: Фесик С.П. "Справочник по сопротивлению материалов" Киев: Будiвельник. - 1982 переход от тангенса к углу упоминается, хотя и без достаточных на мой взгляд объяснений). Более того, если быть совсем уж точным, то таким способом мы определяем отношение продольной деформации к высоте балки Рассчитываемые элементы далеко не всегда имеют прямоугольное сечение, как наша рассматриваемая линейка. В качестве балок и перемычек могут использоваться различные горячекатаные профили, тесанные и не тесанные бревна и вообще все, что угодно. Тем не менее понимание принципов расчета момента инерции позволяет определить момент инерции для поперечного сечения любой, даже очень сложной геометрической формы. В абсолютном большинстве случаев вычислять самому момент инерции нет необходимости, для металлических профилей сложного сечения (уголки, швеллера, двутавры и др.) момент инерции, как впрочем и момент сопротивления определяется по *сортаменту. Для элементов круглого овального, треугольного сечения и некоторых других видов сечения определить момент инерции можно по соответствующей таблице. Если рассматривать суммарную деформацию всей балки, т.е. 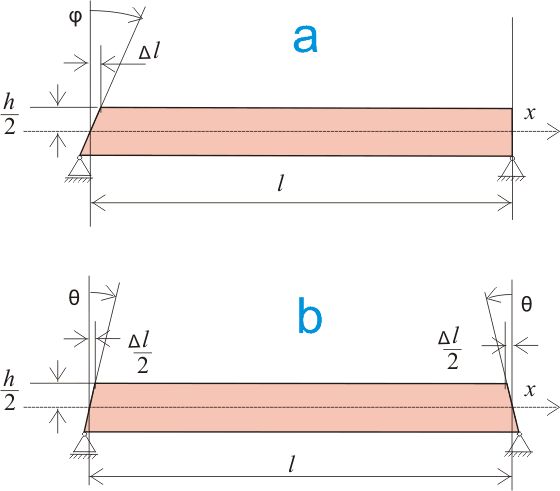по всей длине l, то очевидно, что суммарная деформация при наших нагрузках не может быть только с одной стороны балки, как показано на рисунке 11.3.а: Рисунок 11.3. Так как к нашей балке нагрузка приложена посредине, в результате чего реакции на опорах, возникающие в результате действия нагрузки равны между собой и каждая равна половине приложенной нагрузки, то скорее при этих условиях суммарная деформация будет выглядеть так, как показано на рисунке 11.3.b и тогда в нашем конкретном случае угол наклона поперечного сечения на каждой из опор будет: tgθ = M·х/(2IЕ)* (11.5.5) Пока мы определяли тангенс угла поворота простым графоаналитическим методом и в случае, когда нагрузка к балке приложена посредине, это у нас неплохо получилось. Но варианты приложения нагрузок к балке бывают всякие и хотя суммарная деформация всегда будет равна Δl, но угол наклона поперечных сечений на опорах может быть разным. Если мы присмотримся к формулам (11.5.4) и (11.5.5) повнимательнее, то увидим, что мы умножаем значение момента в некоторой точке на величину х, которая с точки зрения теоретической механики ни чем не отличается от понятия - "плечо действия силы". Получается, что для определения тангенса угла поворота мы должны умножить значение момента на плечо действия момента, и значит, понятие "плечо" можно применить не только к силе, но и к моменту. Когда мы использовали понятие плеча действия силы, открытое еще Архимедом, то мы и предполагали как далеко это может нас завести. Метод, показанный на рисунке 5.3, дал нам значение плеча момента = х/2. Теперь попробуем определить плечо момента другим способом (графоаналитический метод). 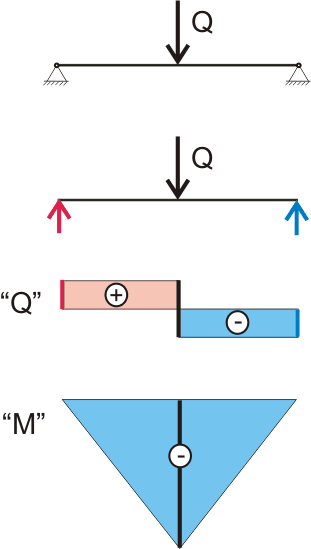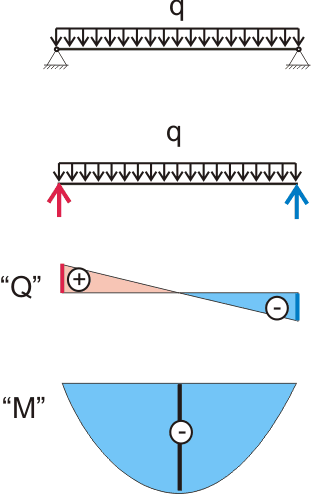Тут нам пригодятся эпюры, построенные для балки на шарнирных опорах: Рисунок 149.7.1 Рисунок 149.7.2 Теория сопротивления материалов позволяет рассматривать внутренние нормальные напряжения, характеризуемые эпюрой "М" рисунка 149.7.1 для балки с постоянной жесткостью, как некую внешнюю фиктивную нагрузку. Тогда площадь эпюры "М" от начала балки до середины пролета - это фиктивная опорная реакция материала балки на равномерно изменяющуюся нагрузку. А фиктивный изгибающий момент - это площадь эпюры "М", умноженная на расстояние от центра тяжести эпюры "М" до рассматриваемой точки. Так как значение изгибающего момента посредине пролета составляет Ql/4, то площадь такой фигуры составит Ql/4(l/2)(1/2) = Ql²/16. А если это значение разделить на жесткость ЕI, то мы получим значение тангенса угла поворота. Забегая наперед, определим значение прогиба. Расстояние от центра тяжести треугольной эпюры "М" до середины пролета равно l/6, тогда фиктивный изгибающий момент составит (Ql²/16)l/2 - (Ql²/16)l/6 = Ql³/48. Тогда прогиб f = Ql³/48EI. А так как эпюра моментов у нас расположена снизу балки, то такая фиктивная нагрузка будет в итоге давать отрицательное значение угла поворота и прогиба, что в общем-то логично, так как при таком действии нагрузки прогиб - смещение центра тяжести поперечного сечения будет происходить вниз по оси у. Примечание: как и с эпюрой моментов, тут есть особенность. Когда эпюра моментов и эпюра прогиба находятся ниже оси балки, то и момент и прогиб считаются положительными. И наоборот, когда эпюра моментов и эпюра прогиба находятся выше оси балки, то и момент и прогиб считаются отрицательными. Для инженеров-строителей это настолько привычно, что они даже не представляют, что может быть по-другому. Характерная особенность графоаналитического метода состоит в том, что количество вычислений можно еще сократить. Для этого нужно умножить площадь эпюры фиктивной нагрузки на расстояние от центра тяжести эпюры до начала координат, а не до рассматриваемой точки на оси. Например, для вышеприведенного случая (Ql²/16)l/3 = Ql³/48 При равномерно распределенной нагрузке эпюра моментов описывается квадратичной параболой, определить площадь такой фигуры и расстояние до центра тяжести сложнее, но для того нам и нужны знания по геометрии, чтобы можно было определить площадь любой фигуры и положение центра тяжести такой фигуры. Впрочем, можно воспользоваться и готовыми формулами. Таким образом получается, что для балки, на которую действует сосредоточенная нагрузка в середине балки при х=l/2: tgθ = М·(x/2)/(ЕI) = ((Ql/4)·(l/4))/(ЕI) = Ql²/(16EI) (11.6.1) То, что мы только что делали называется интегрированием, ведь если умножить значение значение эпюры "Q" (рисунок 149.7.1) на длину действия нагрузки, мы тем самым определим площадь прямоугольника со сторонами "Q" и х, при этом площадь данного прямоугольника равняется значению эпюры "М" в точке х. Теоретически получается, что мы можем определить значение тангенса угла поворота, интегрируя одно из уравнений моментов, составленных для нашей балки. Максимальное значение тангенса угла поворота для балки на двух шарнирных опорах, на которую действует сосредоточенная нагрузка посредине (рисунок 149.7.1), будет при х=l/2 tgθ = ∫Mdx/(EI) = ∫Axdx/(EI)= Ax²/(2EI) = (Q/2)·(l/2)²/(2ЕI) = Ql²/(16EI) (11.6.2) где А - это реакция опоры = Q/2 При распределенной нагрузке интегрирование уравнения моментов: q(l/2)·x - qx²/2 для левой части балки дает следующий результат: tgθ = ∫Mdx/(EI) = q·(l/2)·(l/2)²/(2ЕI) -q·(l/2)³/(6ЕI) = ql³/(24EI) (11.6.3) Тот же результат мы получим и при использовании графо-аналитического метода. Примечание: конечно же все это применимо в чистом виде только в частном случае - для симметричных нагрузок. Когда мы определяли угол поворота, то для наглядности предположили, что балка деформировалась так, как показано на рисунке 5.2, потом так, как показано на рисунке 11.3.b, потом мы выяснили, что если бы второй опоры не было, то балка повернулась вокруг первой опоры, но в действительности вторая опора есть и потому так балка деформироваться (при нашей нагрузке на балку) не может. Так как на опоре нет никакого вращающего момента и соответственно никаких внутренних напряжений, способных изменить геометрическую форму балки, то геометрическая форма балки на опоре остается неизменной, а внутренние напряжения, увеличивающиеся по ходу балки, деформируют балку все сильнее и это приводит к тому, что балка поворачивается вокруг шарнирных опор и этот угол поворота равен углу наклона поперечного сечения θ (так как мы рассматриваем балку-параллелепипед): Рисунок 11.4. Реальная деформация балки. 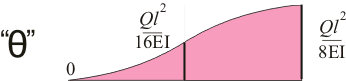Если мы просто постоим эпюру углов поворота для балки со сосредоточенной нагрузкой посредине по уравнениям для левой и для правой части балки, то эпюра будет выглядеть так: Рисунок 11.5. Данная эпюра была бы правильной только для балки, изображенной на рисунке 5.3.а. Очевидно, что в нашем случае эпюра так выглядеть не может и для построения правильной эпюры нужно учесть, что поперечные сечения балки имеют наклон на обоих опорах, причем наклон этот одинаковый по значению, но разный по направлению а наклон поперечного сечения балки посредине =0. 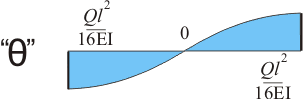Если мы опустим эпюру на Ql²/16EI, которое мы получаем при интегрировании уравнения моментов для левой части балки и которое показывает угол наклона поперечного сечения именно на опоре, то получим эпюру следующего вида: Рисунок 11.6. Данная эпюра абсолютно точно показывает, изменение угла поворота поперечных сечений, вдоль всей балки, а значение тангенса угла поворота на левой опоре балки не что иное, как некая постоянная С₁, которую мы получаем, если интегрирование выполнять корректно. И тогда уравнение угла поворота для балки при данной нагрузке на участке 0<x<0.5l будет выглядеть так: tgθ_х = - tgθ_A + Ax²/(2EI) (11.6.5) Эпюра углов поворота для балки с распределенной нагрузкой визуально ни чем не отличается от эпюры углов поворота для балки со сосредоточенной нагрузкой, разница только в том, что эпюра углов поворота для балки с распределенной нагрузкой - это кубическая парабола. Уравнение угла поворота для балки с равномерно распределенной нагрузкой будет выглядеть так: tgθ_х = - tgθ_A + Ax²/(2EI) - qx³/(6ЕI) (11.6.6) По поводу знаков в данном уравнении. "-" означает, что рассматриваемый член уравнения как бы пытается повернуть балку против часовой стрелки относительно рассматриваемого поперечного сечения, а "+" - по часовой стрелке. Впрочем и по эпюре углов поворота видно, что значение tgθ_А должно быть отрицательным. Таким образом, если сечение имеет наклон по часовой стрелке относительно оси х, то оно будет отрицательным, а если против часовой стрелки - то положительным. Ну и теперь самое главное, все эти разборки с углом поворота поперечного сечения нужны нам были для того, чтобы определить прогиб балки. 12. Определение прогиба. (вернуться к основному содержанию) Как мы видим из рисунка 11.4, треугольник с катетами h/2 и Δх является подобным треугольнику с катетом Х и вторым катетом, равным f+у, а это значит, что теперь мы можем определить значение прогиба: tgθ = (f + y)/Х (12.1) тогда f + y = tgθ·X (12.2.1) или f + y = М·x·Х/(2ЕI) (12.2) при малых значениях х значение у близко к 0, но в более дальних точках сечения значение у увеличивается. Значение у - это и есть влияние на величину прогиба наличия второй опоры. Отметим, что это значение у показывает разницу между реальным наклоном продольной оси балки и наклоном продольной оси балки, если бы балка просто поворачивалась вокруг опоры, и получается, что значение у зависит от изменения угла поворота. Кроме того, мы опять получили уравнение, в котором значение прогиба в некоторой точке зависит от тангенса угла поворота (12.2.1) и таким образом получается, что у угла поворота тоже есть "плечо действия". Например при у=f/2 (если присмотреться к левой части фотографии 1, то посредине балки это где-то так и будет) мы бы получили следующую формулу для определения прогиба: f = М·x²/(3ЕI) (12.3.1) Но мы не будем ничего предполагать, а воспользуемся интегрированием. Если мы проинтегрируем уравнение моментов для левой части балки, то получим значение у (эпюра для у показана бирюзовым цветом на фотографии 1): у =∫∫∫(Q/2)dх = (Q/2)·(l/2)³/6EI = Ql³/(96EI) (12.3.2) или площадь фиолетовой эпюры для левой части балки(рисунок 5.5), но нам нужна площадь голубой эпюры на левом участке балки (рисунок 5.6), которая в 2 раза больше площади фиолетовой эпюры. Таким образом: f =2∫∫∫(Q/2)dх =2 (Q/2)·(l/2)³/6EI = Ql³/(48EI) (12.3.3) Почему площадь голубой эпюры в 2 раза больше площади фиолетовой эпюры, объяснить очень легко. Площадь треугольника равна 1/2 от площади прямоугольника с теми же сторонами, площадь фигуры, описанной квадратной параболой, составляет 1/3 от площади прямоугольника с теми же сторонами. Если бы мы развернули фиолетовую эпюру, то получили бы прямоугольник, образованный голубой и фиолетовой эпюрами. Соответственно, если из площади прямоугольника вычесть 1/3, то мы получим 2/3. У этого логического ряда есть продолжение - площадь фигуры, описанной кубической параболой, составляет 1/4 от площади прямоугольника с теми же сторонами и так далее. Мы можем найти значение прогиба и другим способом. Из рисунка 11.4 и формул (12.2) следует, что: f_х = - tgθx + ∫tgθdx (12.3.4) f_l/2 = - (Ql²/16EI) l/2 + (Ql³/96EI) = -(Ql³/48EI) (12.3.5) В данном случае знак "-" показывает, что центр поперечного сечения балки переместится вниз по оси у относительно оси х. А теперь вернемся к фотографии 1. Под продольной осью балки изображена эпюра у, именно это значение в точке l/2 мы и вычли, решая уравнение (12.3.3). Кроме того получается, что соотношение между f и у зависит от коэффициента предыдущего интегрирования, т.е. у = kf или f = y/k. Когда мы интегрировали уравнение сил, то получили коэффициент 1/2. Впрочем, такое же значение мы получили и тогда, когда определяли плечо действия момента. Если продолжить этот логический ряд, то получается, что при определении прогиба от распределенной нагрузки мы должны использовать коэффициент 1/3, то есть прогиб в середине балки мы можем вычислить по следующей формуле: f= 2∫∫∫(ql/2)dx - 3∫∫∫∫qdх = (2(qlx³/6) - 3(qx⁴/24))/EI = 5ql⁴/(384EI) (12.4.4) или f_х= - ∫tgθdx + ∫∫∫(ql/2)dx -∫∫∫∫qdх (12.4.5) f_l/2 = (- ql³x/24 + (qlx³/6) - (qx⁴/24))/EI = - 5ql⁴/(384EI) (12.4.6) В данном случае знак "-" означает, что центр тяжести поперечного сечения перемещается вниз по оси у. Примечание: Предложенный метод определения прогиба несколько отличается от общепринятых, так как я старался сделать основной упор на наглядность. Если определять прогиб графоаналитическим методом, то площадь фиктивной нагрузки - эпюры моментов, описываемой квадратной параболой, будет составлять (согласно таблице 378.1) (2ql²/(8·3))l/2 = ql³/24. А расстояние от центра тяжести эпюры до начала координат составляет 5/8, Тогда фиктивный момент равен (ql3/24)(5l/(8·2)) = 5ql⁴/384. Конечно же, сосредоточенная нагрузка к балке может быть приложена и не посредине, распределенная нагрузка может быть не только равномерно распределенной и действовать не по всей длине балки, да и варианты крепления балки на опорах бывают разные. Но для того и существуют *готовые формулы, чтобы ими пользоваться. -Позвольте! - Скажете вы, - Все это хорошо, но как быть с касательными напряжениями? Ведь они действуют вдоль оси у и потому должны как-то влиять на прогиб! Все верно. Касательные напряжения действительно влияют на прогиб, однако для балок с соотношением l/h > 10 это влияние очень незначительно и потому допустимо для определения прогиба пользоваться изложенным в данной статье методом. Но это еще не все, как мы уже говорили, определить значение прогиба опытным путем достаточно просто по методу, описанному в самом начале статьи. Так так ничего лучшего под рукой не было, то я взял деревянную линейку, прообраз которой я так долго описывал (см. фотографию 1). Деревянная линейка имела размеры около 91.5 см, ширину b=4.96 см и высоту h=0.32 cм (высоту и ширину определял штангенциркулем). Затем я положил линейку на опоры, при этом расстояние между опорами составило около 90 см и таким образом получил балку с пролетом l=90 см. Под воздействием собственного веса линейка конечно же немного прогнулась, но столь малый прогиб меня не интересовал. Я измерил рулеткой (точность до 1 мм) расстояние от пола до низа линейки (77.65 см), затем приложил посредине условно сосредоточенную нагрузку (поместил посредине мерный стакан весом около 52 грамм с 250 граммами воды) и измерил расстояние от пола до низа линейки при нагрузке (75.5 см). Разница этих двух измерений и составила искомый прогиб. Таким образом величина прогиба определенного опытным путем составила 77.65 - 75.5 = 2.15 см. Осталось только найти модуль упругости для древесины, определить момент инерции для данного сечения и точно посчитать нагрузку. Модуль упругости Е для древесины = 10⁵ кгс/см², момент инерции прямоугольного сечения I_z = bh³/12 = 4.98·0.32³/12 = 0.01359872 см⁴, полная нагрузка - 0.302 кг. Расчет прогиба по формуле дал: f = Ql³/(48EI) = 0.302·90³/(48·10⁵·0.0136) = 3.37 см. Напомню, что прогиб, определенный опытным путем, составил: f = 2.15 см. Возможно следовало учесть влияние на прогиб первой производной функции - тангенса угла поворота? Ведь угол наклона, судя по фотографии, достаточно большой. Проверяем: tgθ = Ql²/(16EI) = 0.302·90²/(16·10⁵·0.0136) = 0.11233. Тогда согласно формулы (542.12) f = 3.37/((1 + 0.112²)^3/2) = 3.307 см. Т.е. влияние конечно есть, но оно не превышает 2% или 0.63 мм. Результат меня сначала удивил, но потом объяснений для такого расхождения нашлось несколько, в частности в середине поперечное сечение линейки было не прямоугольным, так как линейка была деформирована от времени и воздействия воды, соответственно момент инерции для такого сечения больше чем, для прямоугольного, кроме того, линейка изготовлена не из сосны, а из более твердой породы древесины, для которой и модуль упругости следует принимать больше. Да и с научной точки зрения одного результата совершенно недостаточно, чтобы говорить о каких-либо закономерностях. После этого я проверил величину прогиба для деревянного бруска с моментом инерции I=2.02 см⁴, длиной более 2 м при пролете 2 м под нагрузкой 2 кг, приложенной посредине бруска и тогда значение прогиба, определенного теоретическим путем и опытным путем, совпало до десятых долей миллиметра. Конечно, можно было бы и дальше продолжать эксперименты, но так уж получилось, что до меня это уже сделали сотни других людей и получили на практике результаты, очень близкие к теоретическим. А если еще учесть, что идеально изотропные материалы бывают только в теории, то это очень хорошие результаты. 13. Определение угла поворота через прогиб. (вернуться к основному содержанию)* Определить значение угла поворота для шарнирно опертой балки, на которую действует только изгибающий момент M на одной из опор, например на опоре А, казалось бы, проще простого: tgθ_х = - tgθ_A + Мx/(EI) - Аx²/(2ЕI) (13.1.1) где А = М/l, (B = - M/l), но для этого нужно знать угол поворота на опоре А, а мы его не знаем, однако вычислить его помогает понимание того, что прогиб на опорах будет равен нулю и тогда: f_A = tgθ_Bl - Bl³/(6EI) = 0; tgθ_B = - Ml³/(6l²EI) = - Ml/(6EI) (13.1.2) f_B = tgθ_Al + Ml²/(2EI)- Al³/(6EI) = 0; tgθ_A = - Ml/(3EI) (13.1.3) Как видим, угол поворота на опоре к которой приложен изгибающий момент, в два раза больше угла поворота на противоположной опоре, это очень важная закономерность, которая в дальнейшем нам очень пригодится. Когда сосредоточенная нагрузка к балке приложена не по центру тяжести или распределенная нагрузка является неравномерной, то углы поворота на опорах определяются через прогиб, как в вышеприведенном примере. Другими словами - значения начальных параметров определяются в ходе решения дифференциальных уравнений.
На этом пока все. Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору" Для терминалов номер Яндекс Кошелька 410012390761783 Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

На главную

Категории:	Расчет конструкций ::: Основы строймеха и сопромата ::: Базовые понятия
Оценка пользователей:	10.7 (голосов: 15)
Переходов на сайт:	149574
Комментарии:
01-02-2013: Константин Задумал антресоль. Одна из сторон - вдоль комнаты - длинной 3 м 20 см. "Колонн" не хочу, крепеж к потолку тоже. Ну, думаю, надо считать. Вспомнил сопромат - бауманка, обзорный курс. Балки, прОгиб (ударение на "о"), распед. нагрузка. Как считать эпюры - до конца так и не вспомнил =)), но знание принципов освобождает от знания фактов. Нашел вашу статью - большое спасибо. Проникся, расчитал пргиб трубы квадратного счечения, подобрал 80х40, прогиб при расчетных лыжах, детской коляске и 7 коробках инструментов около 6 мм., устраивает. Эксперимент совпал с рассчетами. Посмотрим, что получится. Еще раз спасибо. 01-06-2013: Ильдар А как исходя из всех этих формул визуализировать процесс прогиба? Я хочу написать такую программу, которая бы позволяла рассчитывать прогибы и отображала бы на рисунке, как он происходит. 01-06-2013: Доктор Лом А это уже вопрос не по моей части, программистом я не являюсь и потому ничего конкретного посоветовать не могу. 04-06-2013: Наталья Спасибо за такое доступное, простое изложение материала. Благодаря Вам у меня получилось посчитать все, что нужно. Очень рада, что попала на вашу страницу. Процветайте и преуспевайте. 11-07-2013: NiKK Спасибо! Очень наглядно! У меня такая же балка но она развернута по продольной оси на 55 градусов. Работает как пружина на сжатие. Нужно подобрать оптимальную конфигурацию балки. Сам точно не осилю. Может, кто ни нибудь готов поучаствовать за вознаграждение 11-07-2013: Доктор Лом Почитайте статью: "Расчет деревянной стойки на сжатие. Общие положения." Должно помочь. 09-01-2014: Кирилл Глубокоуважаемый Доктор Лом! Не могли бы Вы рассчитать допустимый прогиб/провис железобетонного перекрытия, рассчёт которого приводили в своей статье https://doctorlom.com/item240.html? 09-01-2014: Доктор Лом Вообще прогиб железобетонных конструкций - отдельный сложный вопрос (все собираюсь написать статью на эту тему), а тем более для плиты, опертой по контуру. Но если очень приблизительно, то для квадратной плиты 5х5 м при максимальной нагрузке прогиб будет до 3.5 см. 16-01-2014: Олег Уважаемый Доктор Лом! Спасибо за хорошие статьи. У меня один вопрос. f измеряется в см. Я подставил размерности в формулу (6.4.6) и после сокращений получилось см^2. В чем проблема? Может l не в той степени и должно быть подобной в формуле (6.3.5)? 16-01-2014: Доктор Лом Возможно в том, что сосредоточенная нагрузка Q измеряется в Ньютонах или килограмм-силах, а линейная равномерно распределенная нагрузка q - в Н/м или кгс/м. 17-01-2014: Олег Спасибо за уточнение, теперь все сходится. 18-03-2014: Dmitry W = I/(h/2) (4.7) или I = W·h/2 что такое I? 18-03-2014: Доктор Лом I - момент инерции. 20-09-2014: Олег Спасибо в очередной раз за прекрасно изложенный материал,- как на лекции побывал (если б в институте знал что изредка сопромат нужен будет по жизни,то б ходил на него с большим усердием - а сейчас это понимаешь, а время то уже упущено, приходится самому ликбезить). Вопрос появился по теме, такого характера - взял я схему самой верхней картинки (балка у меня это коробка из двух 16х швеллеров и опирается краями она на две точки расстояние между которыми 8 метров) и по середине моей балки опирается груз в 200 кг.По прочностным расчетам балка проходит - суммарный момент сопротивления балки (по Wx- как расположена) получается с большим запасом, просчитал прогиб по готовой формуле для этого случая ( f=pl3 /48 EJ) получил прогиб в 1,42 см, который по нормам ниже 1/200 и значит проходит. Но задумался я над тем, что приложенная нагрузка в 200 кг по средине 8ми метровой балки это то да, но у нас же есть еще и собственный вес балки, который так же влияет на прогиб: 16й швеллер у нас весит 14,2 кг/м.п. ( у нас коробка, т.е. их два) и получаем вес балки 14,2 кг/м.п. х 8 м х 2шт = 224 кг, т.е. получается что теперь при расчете прогиба ( с учетом собственного веса балки) мне вес Р (из формулы f=pl3 /48 EJ)необходимо брать равный 200 кг (вес груза) +224 кг ( вес балки) =424 кг. Но берут сомнения за этот вес,потому как большой получается, и кажется что где то я "не там свернул" в своих рассуждениях.Так ли это? 20-09-2014: Доктор Лом Дело в том, что собственный вес балки - это равномерно распределенная нагрузка и прогиб от распределенной нагрузки считается по другой формуле, а затем прогиб от сосредоточенной и от распределенной нагрузки суммируются. 20-09-2014: Олег Спасибо большое за задание вектора, в каком направлении мне делать изыскания. Сегодня нашел формулу и досчитал прогиб балки от собственного веса, но полученный прогиб настолько маленький оказался , что меня взяли сомнения. Я не напрашиваюсь что б мне кто то что то посчитал - просто прошу глянуть на мой расчет и сказать правильно я рассудил или не правильно - а дальше я уже сам буду доходить до истины, в зависимости от ответа.Просто решать решается, а понимающего человека в сопромате который сказал бы -да верно/нет не верно рядом нет, ну а за прорехи института я уже написал ( . Вообщем у нас балка длинной 8 метров, состоящая из сваренных в "коробку" 2х 16х швеллеров (160мм) и по сортаменту металлопроката 1м.п. = 14,2 кг и так как в 1 метре у нас 100 см, то распределенная нагрузка действующая от собственного веса балки будет 0,0142 кг/см ( я перевожу все в кг и см). Теперь формула для равномернораспеределнной нагрузки на балку опирающейся на крайние точки равна : f= (5PL"в 4й степени) / 384 ЕJ. Данные для нее :Р=0,0142 кг/см; L=813 cm; Е=2100000 кг/см2 ; Jx=747 cм4. Далее я проверил формулу на всякий случай по методу размерностей f= (кгсм4см2) / кгсм4см = см - все верно. Теперь расчет : f=(50.0142813813813813) / 3842100000(747х2шт) = 6,8 x 10 в -5й степени см . Ну как мне кажется, ну ооочень маленький прогиб от собственного веса или так оно и есть? Спасибо большое за потенциально возможный ответ,- может на емэил пришлете "да-да" "нет-нет", а то от темы форума я этим комментарием немного отклонился. 20-09-2014: Доктор Лом* В этот раз у вас одна небольшая ошибка: при переводе нагрузки на погонный сантиметр получится 0.142 кг/см, а не 0.0142 (и это похоже нагрузка только от 1 швеллера и в таком случае нужно или умножить нагрузку на 2 или не умножать момент инерции на 2). А дальше у вас большие проблемы с калькулятором, потому что даже в приведенном вами выражении получится около 0.025 см, а с учетом указанной ошибки прогиб от собственного веса составит около 0.51 см. Кстати при расчете прогиба от сосредоточенной нагрузки вы похоже также не учли, что прогибаться будут 2 швеллера и соответственно прогиб будет в 2 раза меньше. А нашу переписку я потом возможно перемещу в отдельную статью и она никого отвлекать не будет. 14-11-2014: Денис Уважаемый Доктор Лом. Поясните, пожалуйста: "Расстояние от центра тяжести треугольной эпюры "М" до середины пролета равно l/6, тогда фиктивный изгибающий момент составит Ql2/16(l/2) - Ql2/16(l/6) = Ql3/48. Тогда прогиб f = Ql3/48EI." Может не фиктивный изгибающий момент, а уравнение фиктивных моментов? Откуда плечо l/2? Спасибо. 14-11-2014: Доктор Лом В данном случае мы определяем именно значение фиктивного изгибающего момента - угла поворота, а уже потом значение прогиба с помощью указанного уравнения. В данном случае плечо l/2 для фиктивной опорной реакции. Более подробно эти особенности расчета рассматриваются в статье "Статически неопределимые балки. Уравнения трех моментов". 16-11-2014: Cергей Уважаемый доктор Лом как рассчитать прогиб для решетчатого прогона или он будет по той же формуле что и для сплошной балки. А как быть с шпренгельной балкой, неужели стойка может быть не меньше 1/6 пролета многовато как посчитать вручную 17-11-2014: Доктор Лом Методика расчета зависит от преследуемой цели. Если вы выполняете расчет для себя и повышенный запас прочности вас не пугает, то это один расчет. А если главная цель - наиболее эффективное использование материалов, то это уже совершенно другой расчет. Судя по всему вы хотите рассчитать конструкцию кровли. Как это сделать, вы можете посмотреть в статье "Расчет стропильной системы и обрешетки. Общие положения". Расчет шпренгельных балок или ферм - отдельная большая тема, да и видов шпренгельных балок не мало. Если хотите упростить расчет, то просто добавьте в расчетную схему шарниры в местах крепления стоек и рассчитывайте вашу конструкцию, как обычную ферму, в противном случае придется возиться со статической неопределимостью системы. А высота стойки теоретически может быть любой. Но чем меньше высота стойки, тем меньше эффективность шпренгеля. И тогда возникает вопрос в целесообразности такого усложнения конструкции. 19-12-2014: Максим Прогиб f=Ql3/4Ebh3 при расчёте в см получается как описано 3,38см. А при расчёте в метрах 0,003386436м или 3,38мм не пойму где ошибка. значения подставлял следующие: Q=0,302кг l=0,9м E=10000000000Па b=0,0496м h=0,0032м 19-12-2014: Доктор Лом Первым делом следует соблюдать размерность. Если вы использовали значение Q в килограммах, то и значение Е следует использовать в кгс/см^2 (1 МПа это приблизительно 10 кгс/см^2) или в кгс/м^2. Возможно в этом ошибка. 29-12-2014: Алина Дом 4-х этажный , перекрытия деревянные, идешь по комнате- шкафы дребезжат .Что делать? 29-12-2014: Доктор Лом Для начала прочитайте статью "Прогиб пола при ходьбе", ну а после решайте, что лучше: или перебирать и усиливать перекрытие, или крепить прочно шкафы к стенам или ходить мягко и осторожно, как кошка. 20-11-2015: Слава Если Вы плохо освоили сопромат, зачем учить и вводить в заблуждение других? Для работы в упругой области напряжения не должны превосходить предела упругости. Напряжения, равные модулю Юнга, в сотни раз превосходят предел прочности. Читайте учебник. 20-11-2015: Доктор Лом Пациент, успокойтесь и просто послушайте, что я вам скажу, возможно это вам поможет. Во-первых, подробному определению модуля Юнга посвящена отдельная статья и на эту статью есть ссылка. Во-вторых, за одно только высказывание "напряжения, равные модулю Юнга" вас следовало бы сразу отправить в палату для буйных, чего я конечно же делать не стану из соображений человеколюбия. Запомните и передайте другим: модуль упругости - это не просто напряжения, а напряжения, деленные на отношение абсолютной деформации к начальной длине ?l/lo (в итоге получается безразмерная величина, которую я для простоты изложения выразил просто как относительную деформацию ?, соответственно и напряжения и расчетные сопротивления и модули упругости измеряются в Па, кгс/см^2 и т.п.). Именно поэтому для некоторых материалов значение модуля упругости в сотни раз больше предела прочности. И еще, вести речь о постоянном значении модуля упругости имеет смысл только в области упругих (пропорциональных) деформаций. В области пластических деформаций значение модуля упругости будет уменьшаться тем стремительнее, чем больше будет становиться относительная деформация. Так что учебник читать нужно не мне, а вам и двойка в данном случае тоже вам. 21-11-2015: Слава Прежде чем раздавать двойки другим, вдумайтесь сами о чем пишете. "модуль Юнга показывает отношение расчетного сопротивления материала!!! (см. часть 2) к относительной деформации". Причем здесь расчетное сопротивление? В статье, на которую Вы ссылаетесь, правильно написано, что модуль Юнга есть отношение нормального напряжения к относительной продольной деформации (в области упругих деформаций). Только надо уточнить, что деформация здесь - это не произвольная деформация, а деформация, соответствующая рассматриваемому напряжению. Студенты выполняют лабораторную работу "Определение модуля Юнга", выполняя нагружение стальной полосы до 40 МПа, что намного меньше расчетного сопротивления. И не корректно модуль Юнга определять через расчетное сопротивление - этого не сделано ни в одном учебнике сопромата, скорее, это Ваша опечатка или фантазия, не знаю. То, что модуль упругости может быть касательным или секущим, мне известно и без ваших ссылок, только в данном абзаце речь идет об упругой работе материала, а там он считается постоянным, и в справочниках даны значения именно для этого случая, и там они никакие не переменные, а константы. В учебнике А.В.Александрова "Сопротивление материалов" (2008 г., с.52)так и написано: "Отметим, что модуль упругости Е является физической постоянной материала". О чем спор? Что касается командировки в палату, так "напряжения, равные модулю Юнга" следуют из вашей же формулы (5.1.2), где присутствует знак равенства. Приведите мне хотя бы один реальный пример для строительных материалов, в котором будет знак равенства в указанной формуле! Впрочем, во фразе "напряжения, равные модулю Юнга" нет никакого внутреннего противоречия: второкурсникам, только начинающим изучать сопромат, известно, что модуль Юнга численно равен таким мысленно представляемым напряжениям при растяжении образца, при которых длина образца увеличивается вдвое (в предположении, что при таких деформациях образец не разрушается и сохраняется закон Гука). Такой вывод сразу следует из закона Гука и приведен в некоторых учебниках. Другой вопрос, что для подавляющего большинства материалов такой уровень напряжений недостижим. Модуль Юнга имеет размерность напряжений, и может сравниваться с ними. Опять о чем спор? Почему на мое замечание о модуле упругости нет ответа? Согласны с ним или тоже будете оспаривать? 21-11-2015: Доктор Лом То есть весь этот поток гневных обвинений из-за того, что вместо понятия "напряжения" я использовал понятие "расчетное сопротивление"? Что ж претензия принимается, тем более с академической точки зрения вы совершенно правы, но. 1. К чему мы стремимся при расчете по первой группе предельных состояний? Правильно, к тому, чтобы нормальные напряжения в рассматриваемом поперечном сечении не превышали расчетного сопротивления, а в идеале были равны. Второй вопрос: когда мы определяем прогиб (выполняем расчет по второй группе предельных состояний)? Правильно, как правило после того, как выполнен расчет по первой группе предельных состояний, т.е. когда нормальные напряжения близки к расчетному сопротивлению или даже равны. Т.е. приведенная мной формула не просто возможна, а наиболее вероятна для множества расчетов. И если вы обратили внимание данная статьи идет, как продолжение другой статьи и начинается с пункта 5. И последний вопрос: часто ли при расчете строительных конструкций по второй группе предельных состояний учитывается то, что расчетное сопротивление материала как правило больше предела пропорциональности и даже предела упругости, а значит и принимаемый для расчетов модуль Юнга должен быть меньше, т.е. должны учитываться пластические деформации? 2. Конечно же, это только частный случай, использование понятия "расчетное сопротивление" - в данном случае не корректно, ничего не поделаешь, я тоже не Демосфен и свои мысли излагаю не всегда ясно. Однако для меня намного более важно донести до читателей мысль о том, что расчеты по первой и по второй группе предельных состояний - это не разные миры, а вполне взаимосвязанные между собой вещи. К сожалению, когда я изучал сопромат, до меня эту мысль так никто и не донес. 3. Я внес поправку в определение физического смысла модуля упругости и если бы более внятно излагали свои мысли, то возможно сделал бы это сразу. Но если вы будете формулировать свои мысли так, как первый раз, то будете получать ответы такие же, как и в первый раз. 4. Из формулы (5.1.2) следует, что нормальные напряжения, деленные на относительную деформацию, не должны превышать значение модуля Юнга, но никак ни "напряжения, равные модулю Юнга". 5. То, что модуль Юнга имеет такую же размерность, как напряжения, не дает никакого основания их сравнивать, а тем более уравнивать (именно это в первый раз меня больше всего и зацепило). Вдумайтесь сами, что вы говорите: "Напряжения, равные модулю Юнга, в сотни раз превосходят предел прочности". Как только нормальные напряжения в рассматриваемом сечении превышают предел прочности даже не в сотни раз, а всего на несколько процентов (или десятков процентов) - наступает разрушение материала. Кстати о процентах. Есть такие понятия: "депозит" и "проценты по депозиту" и хотя и то и другое в конечном итоге измеряется в рублях, но все равно это совершенно разные понятия и пользоваться ими нужно правильно. 17-03-2017: Эмин Я что то не понял,почему мы прикладываем силу по высоте балки?вообще запутался 17-03-2017: Доктор Лом Скорее всего вы имеете в виду рисунок 507 или 149. Объяснения этому даются в соответствующих статьях. Ссылки на них есть в содержании. А вообще лучше начать с самого начала. 08-06-2017: Дастан Здравствуйте, Доктор Лом! через напряжения или через прогиб то есть перемещение как можно определить момент? и поперечную силу. например я считал какой то программе из объемных элементов не линейным. и там получил нормальные и касательные напряжения и перемещение. и этих данных как можно перейти на внтренные усилия что бы сделать подбор арматуры 11-06-2017: Доктор Лом Через напряжения проще, но можно и через прогиб. А нормальные и касательные напряжения - это и есть внутренние усилия в рассматриваемом поперечном сечении. 20-01-2018: Leo У меня такой вопрос . При равномерно распределённый нагрузке по длине л площадь эпюры изгибающего момента равно 2/3 ql^2/8 l. Здесь ql^2/8 это экстремум функции. А как получается коефицент 2/3? 20-01-2018: Доктор Лом Возможно следующий абзац из текста статьи даст ответ на ваш вопрос: "Площадь треугольника равна 1/2 от площади прямоугольника с теми же сторонами, площадь фигуры, описанной квадратной параболой, составляет 1/3 от площади прямоугольника с теми же сторонами. Если бы мы развернули фиолетовую эпюру, то получили бы прямоугольник, образованный голубой и фиолетовой эпюрами. Соответственно, если из площади прямоугольника вычесть 1/3, то мы получим 2/3. У этого логического ряда есть продолжение - площадь фигуры, описанной кубической параболой, составляет 1/4 от площади прямоугольника с теми же сторонами и так далее." 28-10-2020: Антон Уважаемый доктор Лом. Я полагаю что в формуле 12.3.2 ошибка (результат интегрирования умножен на 2 как в формуле 12.3.3). А так же в описание под этой формулой ссылка на рисунок 11.5 и 11.6, а не на 5.5 и 5.6. 28-10-2020: Доктор Лом Никакой ошибки нет. Еще раз внимательно посмотрите на формулы, на указанные рисунки и вспомните, как определяется площадь квадратной параболы, если она имеет такой вид, как на рисунке 11.6. 29-10-2020: Антон Так я говорю не об ошибке формуле по рисунку 11.6, а по рисунку 11.5. Я про формулу 12.3.2 - в том исполнении, что написано у Вас (с 2 перед скобками после знак =) ответ получается Ql3/(48EI) 29-10-2020: Доктор Лом Точно, Антон, протупил (копипаст не проконтролировал). Исправил. Спасибо за внимательность (просто с временем сейчас реально напряг, вчера быстро пробежал ваше сообщение по диагонали, ну и накосячил). Обидно только, что статью уже больше 120 000 пользователей прочли, а об опечатке вы мне первый сообщаете. Ну ничего, теперь вы не просто один из сотни тысяч читателей, теперь вы, Антон, - Первый Внимательный и Требовательный Читатель. За это вам от меня - респект и уважуха. Не знаю, будет ли вам интересно, но я тут тоже у одного авторитета в законе косяк нашел. И там тоже с двойками напутано (совпадение? не думаю). Поэтому и времени в обрез. 30-10-2020: Антон Спасибо Вам большое за ваш труд,а так же за то что вы читаете и отвечаете на комментарии читателей. Этот материал очень мне помагает в работе. Извините за назойливость, но и в дальнейших формулах у меня возникают нестыковки : В формуле 12.3.4 (fх = - tgθx + ∫tgθdx),я не могу понять, почему результат интегрирования (tgθ = Ql2/16EI) у Вас получился - (Ql3/96EI). В формуле 12.4.4 (f= 2∫∫∫(ql/2)dx - 3∫∫∫∫qdх ), я так понимаю кол-во знаков ∫ - это кол-во интегрирований. У меня получается равенство только при результате (2(qlx3/12) - 3(qx4/24))/EI = 5ql4/(384EI). У вас в начале уравнения стоит 2(qlx3/6 - ... та же самая ситуация с формулой 12.4.6, равенство получается если (- ql3x/24 + (qlx3/12) - (qx4/24))/EI = - 5ql4/(384EI). И, возможно я испорчу мнение о себе, но начиная с формулы 12.3.4 и дальше я перестал понимать каким образом вы выводите данные формулы. Заранее спасибо за ответ 30-10-2020: Доктор Лом Антон, я уже говорил, у меня времени в обрез. Поэтому очень коротко. Я просто определяю площади фигур. Это значительно быстрее и нагляднее, чем заниматься интегрированием в чистом виде. В том виде, в каком вы записали, это результат интегрирования уравнения угла поворота, а в уравнении угла поворота есть некая постоянная величина С, в данном случае - начальный угол поворота. Потому что, что? Потому что уравнение углов поворота - это результат интегрирования уравнения моментов. Я об этом рассказывал где-то по ходу курса, именно поэтому в начале каждой статьи есть содержание. И я потратил полдня на то, чтобы вставить это содержание в каждую статью не потому, что мне нечем заняться. Я этим как бы намекнул, что если вам что-то непонятно, то имеет смысл прочитать цикл с самого начала. Просто читайте и думайте, вот буквально с первых фраз: "По большому счету сопромат даже проще, чем таблица умножения". Спешить не надо. Я старался изложить материал с минимальным использованием всяких математических заумностей типа дифференциалов-интегралов, необходимых в общих случаях, а больше напирал на частные случаи, как более доступные для понимания и на графические образы. А знак равно после четырех интегралов кряду как раз и показывает, что иногда можно обойтись и без дурной работы, ежели понимаешь, что к чему.
Добавить свой комментарий: Имя: E-Mail адрес: Комментарий: Ваша оценка:
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).

35215208680f6fbd