Содержание:
Основы сопромата кратко.
1. Виды опор.
1.1. Шарнирные опоры.
Расчетная длина (пролет) балки.
1.2. Опорные связи шарнирно закрепленной балки.
1.3 Жесткое защемление на опорах.
1.4. Скользящие заделки.
2. Нагрузки (внешние силы).
3. Напряжения (внутренние силы).
4. Реакции опор.
5. Уравнения статического равновесия.
4.1. Определение опорных реакций.
6. Уравнения изгибающего момента.
7. Балка на двух шарнирных опорах.
8. Консольная балка.
9. Метод сечений.
10. Определение момента сопротивления.
11. Определение угла поворота.
12. Определение прогиба.
13. Определение угла поворота через прогиб.
14. Список использованной литературы.
Если совсем кратко, то основы сопромата, изложенные в данной статье, звучат так:
- Любое физическое тело может быть строительной конструкцией
- У любой конструкции есть опоры
- Опоры обеспечивают статическое равновесие системы.
- На любую конструкцию действуют силы.
- Эти силы могут быть внешними, т.е. действующими снаружи конструкции (такие силы называются нагрузками) и внутренними, действующими внутри конструкции (такие силы называются напряжениями).
- Однако с точки зрения физики никакой разницы между внешними и внутренними силами нет - мы всегда можем заменить внешние силы на внутренние и внутренние на внешние, главное, чтобы при этом соблюдалось статическое равновесие системы.
- Метод, позволяющий определить напряжения в различных точках конструкции, называется методом сечений.
- Напряжения в любой точке конструкции должны быть меньше расчетного сопротивления материала конструкции.
Вот в принципе и все, далее следуют формулы и прочие расчеты, но попробуем добавить больше наглядности этим положениям на примере балки.
Чтобы наглядно представить себе основы сопромата, достаточно иметь две простых школьных деревянных линейки, например, длиной 20 и 40 см и несколько книг, учебники по сопромату подойдут здесь как нельзя лучше, и стол. Впрочем можно иметь и одну пластмассовую или алюминиевую линейку любой длины и книги любого содержания.
1. Виды опор.
Теперь нужно положить линейку плашмя на два выступа, например на 2 книжки:

Рисунок 1.
Если посмотреть на линейку сбоку, то будет видно не только название учебника, но и то, что линейка лежит плашмя.
1.1. Шарнирные опоры
(вернуться к основному содержанию)
С одной стороны все вроде бы просто, лежит себе линейка на книгах, ну и пусть лежит, а вот если взглянуть на эту ситуацию с точки зрения теоретической механики (до сопромата мы пока еще не добрались), то мы с Вами имеем не обычную школьную линейку, лежащую на книгах, а модель балки на двух скользящих шарнирных опорах и выглядеть это будет так:

Рисунок 2.1
1.1. Кольца на концах балки - это шарниры, вокруг которых балка может свободно вращаться и если мы уберем например книгу справа, то левый конец линейки условно останется на месте, а правый свободный конец линейки упадет на стол, т.е. линейка повернется и значит наше допущение, что опоры шарнирные, правильное.
1.2. Горизонтальные линии с косой заштриховкой снизу означают некое устойчивое основание, в данном случае это стол.
1.3. Некоторое расстояние между основанием и опорами балки, обозначенными треугольниками, является неким подобием воздушной подушки и означает, что опоры могут скользить по основанию без трения.
Скользящие шарнирные опоры не позволяют перемещаться концам балки только относительно оси у, т.е. создают только одну опорную связь - вертикальную.
1.4. На самом деле у нашей линейки нет никаких шарниров, связывающих ее с опорами, а опирается линейка, если очень хорошо присмотреться, на выступающие корешки книг и можно изобразить нашу линейку например так:

Рисунок 2.2
В технической литературе такое отображение опор (без шарниров) также встречается и означает, что опоры не препятствуют повороту, но препятствуют перемещению по вертикали и по горизонтали.
И действительно, если мы попробуем передвинуть линейку вправо или влево, то для этого нужно приложить силу, большую чем сила трения, возникающая между линейкой и книгами в результате действия силы тяжести на линейку. Таким образом опоры, показанные на рисунке 2.2 могут рассматриваться как шарнирные неподвижные (нескользящие) опоры. Соответственно такие опоры создают две опорные связи - вертикальную и горизонтальную.
1.5. на рисунке 2.1 шарниры находятся на концах балки, на рисунке 2.2 треугольники опор находятся на некотором расстоянии от концов балки. С точки зрения теоретической механики никакой разницы тут нет, если принимать расстояние между опорами и на рисунке 2.1 и на рисунке 2.2 одинаковым, а на концы линейки, находящиеся за пределами опор, ни какая нагрузка не действует.
Расчетная длина балки
(вернуться к основному содержанию)
Это означает, что реальная длина балки и расчетная длина балки - это не одно и то же. Реальная длина балки всегда больше расчетной длины, а расчетная длина балки - это расстояние между опорами, в данном случае просвет между книгами. Длина балки измеряется по оси х.
Расчетная длина (пролет балки) обозначается литерой l.
Концы линейки, опирающиеся на книги, можно рассматривать как опорные участки балки lоп. Расчет опорных участков балки на смятие - отдельная большая тема, но в данном случае мы только постигаем основы сопромата и на этом этапе нам достаточно знать, что чем больше длина опорных участков, тем лучше для балки, а реальная длина балки составляет:
lp = l + 2lоп (1.1)
1.2. Опорные связи шарнирно закрепленной балки
(вернуться к основному содержанию)
Любое физическое тело, в данном случае линейка, имеет три степени свободы движения в рассматриваемой плоскости ху: 1) тело может перемещаться вдоль оси х, 2) тело может перемещаться вдоль оси у, 3) тело может вращаться вокруг некоторой точки, даже если свобода перемещения относительно осей х и у ограничена.
Соответственно любая устойчивая и статически определимая конструкция должна иметь как минимум три опорных связи, ограничивающих указанные степени свободы. Балка, показанная на рисунке 2.1, является статически определимой, но не устойчивой, так как у нее только 2 параллельные вертикальные связи. Балка, показанная на рисунке 2.2, является устойчивой, но статически неопределимой, так как у нее 2 вертикальные и две горизонтальные опорные связи. А уравнения статического равновесия позволяют определить только три неизвестных величины (об этом чуть позже).
Поэтому в технической литературе часто встречается следующее отображение шарнирных опор балки:
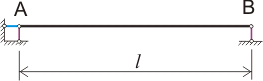
Рисунок 2.3
Физический смысл такого отображения опорных связей следующий:
1. Любая однопролетная статически определимая балка (а наша балка, сразу скажу, является и однопролетной и статически определимой) имеет две вертикальные опорные связи (на рисунке 2.3 показаны фиолетовым цветом) и одну горизонтальную связь (на рисунке 2.3 показана голубым цветом). При этом направления связей не пересекаются в одной точке, поэтому балка является устойчивой, а в целом система из 4 стержней - геометрически неизменяемой.
2. Эти связи шарнирно соединены не только с балкой но и с неким жестким основанием. А это в свою очередь означает, что не только балка может свободно поворачиваться относительно опорных связей, но и опорные связи могут свободно поворачиваться относительно жесткого основания.
3. Для обеспечения геометрической неизменяемости (устойчивости) системы горизонтальная опорная связь необходима, хотя при расчетах на вертикальную нагрузку она вроде бы и не нужна, но это уже отдельная история.
4. Стержни, обозначающие вертикальные и горизонтальную связи - это большая условность, и нужны они лишь для того, чтобы на первом же этапе расчета заменить их соответствующими опорными реакциями. Условно эти стержни рассматриваются, как бесконечно жесткие, т.е. деформация таких стержней при любой нагрузке равна нулю.
5. Таким образом вертикальная опорная связь на опоре В, показанная ни рисунке 2.3, препятствует только вертикальному перемещению балки в точке В и соответствует скользящей шарнирной опоре, показанной на рисунке 2.1. Такая опора в точке В называется шарнирно подвижной опорой.
6. Вертикальная связь на опоре А препятствует вертикальному перемещению балки в точке А, а горизонтальная связь - горизонтальному перемещению балки. Такая опора в точке А называется шарнирно неподвижной опорой и соответствует рисунку 2.2.
Казалось бы, для нашей линейки такое отображение опорных связей не подходит, никакой ярко выраженной горизонтальной связи у линейки по умолчанию нет (за исключением сил трения), но тут все зависит от того, какие именно задачи предстоит решать.
Достаточно часто балки рассчитываются на вертикальную нагрузку, действующую вдоль оси координат у, при этом никаких сил, действующих вдоль оси координат х, нет или их сумма равна 0. Кроме того, если приложенные горизонтальные нагрузки будут меньше, чем силы трения, возникающие на опорных участках балки под действием вертикальной нагрузки, то в таких случаях схема балки, приведенная на рисунке 2.3, для нашей линейки вполне допустима.
1.3 Жесткое защемление на опорах
(вернуться к основному содержанию)
Если пригрузить концы линейки еще книгами:

Рисунок 3.
то такую линейку можно условно рассматривать, как балку, защемленную на опорах, и тогда модель балки будет выглядеть так:
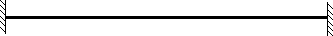
Рисунок 3.1
Физический смысл такого отображения опор следующий: жесткая заделка препятствует не только вертикальному и горизонтальному перемещению балки на опоре, но также и повороту. т.е. ограничивает все 3 степени свободы физического тела. Такая опора называется жестким защемлением или глухой заделкой.
Мы можем легко в этом убедиться, если уберем одну из стопок книг. Линейка, защемленная в другой стопке, останется на месте.
Опять же в данном случае рассматривать балку как жестко защемленную не совсем правильно, если опорные участки достаточно короткие, а вот если книги с линейкой хорошо проклеить, и опорные участки у линейки сравнительно длинные, то после высыхания клея линейку уже можно рассматривать как балку, жестко защемленную на опорах.
Но все равно чаще всего при расчетах принимается вариант опор, показанный на рисунке №2.3. А вот железобетонные балки, которые бетонируются одновременно со стенами или металлические балки, жестко приваренные или прикрученные к очень жесткому основанию так, что составляют как бы единое целое, можно рассматривать как балки, защемленные на концах.
1.4. Скользящие заделки
(вернуться к основному содержанию)
Жесткая заделка на опорах может быть не только глухой, но и скользящей, в чем мы легко можем убедиться, если толкнем одну склеенную стопку книг по горизонтали в направлении линейки, при этом вторая стопка книг будет непроклеенной, или, если обе стопки проклеенные, попробуем одну стопку приподнять так, чтобы угол поворота на защемленном этой стопкой конце линейки не менялся. В первом случае мы получим жесткую заделку, скользящую по горизонтали, а во втором - по вертикали. Опорные связи при этом более правильно отображать так:

Рисунок 3.2. а) заделка, скользящая относительно оси х; б) заделка, скользящая относительно оси у.
Т.е. одна из склеенных стопок книг нами по-прежнему рассматривается как глухая заделка на опоре А, а вот заделки на опоре В уже рассматриваются как скользящие. Такие заделки называются скользящими заделками или жесткими заделками с одной степенью свободы перемещения.
Но и это еще не все, скользящая заделка может иметь сразу две степени свободы перемещения, т.е. не ограничивать перемещение рассматриваемого конца балки ни по вертикали ни по горизонтали, единственное, что при этом ограничивается, - это угол поворота. Такая заделка называется бискользящей или жесткой заделкой с двумя степенями свободы перемещения.
1.5. Если продолжить мысль и представить, что наша линейка очень прочно склеена из отдельных кусочков, то получается, что мы можем рассматривать любой участок нашей линейки, например, между отметками 5 и 15 см, как отдельную балку со скользящей заделкой на концах и могли бы изобразить нашу балку не как одну балку на двух шарнирных опорах, а как 2, 3 и сколь угодно много балок, из которых крайние балки имели бы по одной шарнирной опоре и на втором конце скользящую заделку, а все остальные балки имели бы скользящую заделку. В данном случае в таком усложнении задачи нет никакой необходимости, но часто такое допущение позволяет решать достаточно сложные задачи.
А чтобы такое предположение было корректным, мы для упрощения решения задачи должны рассекать нашу балку очень аккуратно в плоскости, перпендикулярной оси х и таким образом мы получим сколь угодно большое количество поперечных сечений балки. Зачем нужно рассматривать поперечные сечения, мы узнаем чуть позже.
Таким образом главное отличие шарнирных опор от жестких заделок в том, что шарнирные опоры позволяют балке поворачиваться на рассматриваемой опоре, а заделки - не позволяют.
Все. Больше никаких вариантов опор при решении задач по расчету строительных конструкций не рассматривается: или шарнирные опоры или заделка (защемление) на концах. Другое дело, что шарнирных опор у балки может быть сколь угодно много, один конец может быть защемлен, опоры, как шарнирные таки и жесткие, могут быть скользящими, шарнирные опоры могут давать осадку и даже представлять собой сплошное упругое основание, у балки могут быть консоли, но это уже варианты не опор, а варианты расположения и комбинации опор. Таких комбинаций может быть бесконечно много, но это уже не основы теоретической механики и здесь мы эти варианты рассматривать не будем.
Ну а теперь выясним, зачем нужно было городить эту конструкцию и что она нам дает.
2. Нагрузки (наружные силы).
(вернуться к основному содержанию)
Если повнимательнее присмотреться к рисунку 1, то можно увидеть, что линейка немного прогнулась посредине. Если взять более длинную 40-сантиметровую линейку и опереть ее на книги, то прогиб посредине линейки будет еще более заметным, но все равно пока не очень явным.
Почему же это случилось?
Оказывается, на линейку действует нагрузка - собственный вес линейки и под действием этой нагрузки линейка прогибается, при этом наибольший прогиб мы можем видеть посредине. Причем, чем больше расстояние между опорами - l, тем меньше несущая способность балки при одном и том же сечении и получается, что расчетная длина балки - очень важный фактор при расчетах. Так как линейка имеет простую параллелепипедную форму и плотность материала, из которого изготовлена линейка приблизительно одинаковая, то такая нагрузка считается равномерно распределенной и на расчетных схемах изображается так:
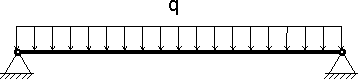
Рисунок 5.
2.1. Распределенная нагрузка может быть равномерной, как показано на рисунке 5, так и неравномерно распределенной, при этом значение распределенной нагрузки может изменяться линейно и не линейно, кроме того распределенная нагрузка может действовать не на всю длину балки, а на один или несколько участков. Если на балку действует несколько равномерно распределенных нагрузок, например: собственный вес, вес от кирпичной кладки, опирающейся на балку, и нагрузка от плит перекрытия то такие распределенные нагрузки можно суммировать, что в дальнейшем значительно облегчает расчеты. Подобный подход называется принципом суперпозиции.
2.2. Если у Вас есть палец, а я думаю, таковых у Вас имеется немало, то при надавливании пальцем на середину линейки линейка прогнется уже значительно заметнее. В этом случае на линейку действует кроме равномерно распределенной нагрузки еще и сосредоточенная (точечная) нагрузка (на рисунке 6 распределенная нагрузка не показана):

Рисунок 6.
Само собой точечных нагрузок может быть сколь угодно много и прикладываться они могут в любом месте балки и не только перпендикулярно оси балки, но и параллельно. Если сосредоточенная нагрузка приложена перпендикулярно на опоре, то на балку это никак не повлияет, просто возникнет реакция опоры численно равная нагрузке и направленная противоположно. Вы можете это легко проверить сами, надавив пальцем на линейку в месте опоры на одну из книг, если уж очень сильно давить, то Вы скорее промнете книгу, но линейка все равно не прогнется.
Почему так происходит?
Оказывается нагрузка, действуя на балку, создает изгибающий момент, т.е. хочет повернуть балку вокруг опор. При этом значение изгибающего момента напрямую зависит не только от величины нагрузки, но и от плеча действия силы. Нетрудно догадаться, что максимальный изгибающий возникает тогда, когда сосредоточенная нагрузка действует на балку посредине.
Конечно же действует этот момент на балку не просто так, а в рассматриваемом поперечном сечении балки и возникает он в данном случае от действия опорной реакции, которую еще следует определить, но об этом разговор пойдет дальше.
Иногда при расчетах вводится понятие вращающего момента, действующего на балку:
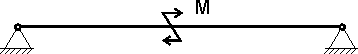
Рисунок 7.
Все, больше никаких вариантов нагрузок, действующих на балку, при решении задач по расчету строительных конструкций не рассматривается. Впрочем, классификация нагрузок - наружных сил - это отдельная большая тема.
Ну и теперь непосредственно сам сопромат, потому как до этого описывались термины и понятия теоретической механики.
3. Напряжения (внутренние силы).
(вернуться к основному содержанию)
Если на линейку, опертую на книги, как показано на рисунке 1, продолжать давить пальцем, то линейка будет прогибаться все сильнее и сильнее, пока в один прекрасный момент не поломается (конечно, вместо грубой физической силы Вы можете использовать мощь своего интеллекта, я возражать не буду)
Почему это происходит?
Оказывается всему есть предел и в данном случае был преодолен предел сопротивления материала (древесины), из которого изготовлена линейка.
Если к примеру взять стальную полосу с такими же параметрами сечения и такой же длины, как у деревянной линейки и тоже положим ее на книги и приложим к ней такую же нагрузку посередине, то поломать стальную полосу пальцем уже вряд ли получится, как минимум потому, что сопротивление стали в десятки раз больше сопротивления древесины. Но вернемся к рассмотрению деревянной линейки.
Когда Вы давите пальцем на линейку, то линейка деформируется, верхняя часть линейки сжимается и, соответственно в этой области возникают сжимающие нормальные напряжения. Нижняя часть линейки растягивается и, соответственно в этой области возникают растягивающие нормальные напряжения. Эти напряжения являются реакцией материала на действующую нагрузку.
Нормальными называются напряжения, направленные по нормали (перпендикулярно) рассматриваемому поперечному сечению балки.
Кроме нормальных в рассматриваемых сечениях могут возникать и касательные напряжения, а еще напряженные состояния могут быть не только линейными, но еще плоскими или объемными, но об этом опять же не сейчас.
Теория сопротивления материалов предполагает, что при таком действии нагрузки в середине поперечного сечения балки деформация равна 0 и, соответственно, никаких нормальных напряжений, ни растягивающих, ни сжимающих в середине поперечного сечения балки нет, а максимальные напряжения возникают посредине пролета балки сверху и снизу поперечного сечения. При этом эпюры внутренних нормальных напряжений в поперечных сечениях балки будут выглядеть так:

Рисунок 8.
Разрушение конструкции может начинаться как в верхней так и в нижней части. Расчет конструкции на прочность сводится к тому, чтобы этого самого разрушения не допустить. Другими словами, максимально возможные напряжения должны быть меньше сопротивления материала. В данном случае:
σ < R (1.2)
Но еще не вечер, надеюсь, линейку Вы не поломали, потому что пришло время опереть линейку на книги не горизонтально, а вертикально:

Рисунок 9.
В таком положении линейку трудно поломать не только пальцем, но и ногой. А мы всего-то повернули линейку на 90°. Площадь сечения балки при этом не изменилась, нагрузка не изменилась, изгибающий момент не изменился, перед нами все та же деревянная линейка.
Почему это происходит?
Теория сопротивления материалов объясняет это чудо так: когда мы повернули линейку, то ширина b лежащей плашмя линейки стала высотой h линейки, поставленной на ребро, а значит изменился расчетный момент инерции, момент сопротивления и, соответственно, несущая способность балки.
В целом в этом и состоит суть сопромата: правильное определение нагрузок, действующих на строительную конструкцию и подбор оптимального сечения конструкции.
Вот и все. Как видите, основы сопромата действительно проще, чем таблица умножения, это просто я их тут слишком подробно расписал. Далее следуют основные формулы, разобраться с которыми тоже в общем-то не сложно на примере той же линейки.
(вернуться к основному содержанию)
Список использованной литературы:
1. Александров А.В. Сопротивление материалов. Москва: Высшая школа. - 2003.
2. Фесик С.П. Справочник по сопротивлению материалов. Киев: Будiвельник. - 1982.
3. Prof. Dr. Ing. Vasile Szolga. Theoretical mechanics, Lecture notes and sample problems - 2010. | 
