
Рисунок 313.1
Если просто разделить 8 м на количество пролетов, равное 5, то мы получим длину пролета между промежуточными опорами 8/5 = 1.6 м. И это было бы справедливо, если бы ширина ребер стремилась к нулю и тогда расчетная схема соответствовала бы реальной конструкции. Однако у нас имеются вполне конкретные балки - ребра шириной 11 см и если ребра с плитой будут бетонироваться одновременно, то расчетный пролет между опорами такой плиты может приниматься 151.2 см (расстояние в свету между опорами). Такой расчетный пролет принимается для того, чтобы упростить расчет по следующим причинам:
1. Чтобы максимально приблизить расчетную схему к реальности, следует рассматривать реакцию промежуточных опор не как сосредоточенную силу, а как нагрузку, распределенную по ширине балки - ребра. Причем нагрузка эта не обязательно будет равномерно распределенной.
2. Так как высота плиты в точках промежуточных опор значительно больше (за счет ребер), то и требуемое сечение арматуры для такого сечения будет меньше.
Тем не менее иногда многопролетные балки имеют постоянную высоту сечения по всей длине, например доска пола, укладываемая по лагам. В таких случаях расчет с использованием длин пролетов в свету будет не совсем точным, однако вполне допустимым, небольшой запас прочности никогда не помешает. Тем не менее хочется иметь хотя бы некоторое представление, о каком запасе прочности идет речь. Так как иногда заглядываешь в сортамент, а там момента сопротивления чуть-чуть не хватает до требуемого, а принимать следующий, обеспечивающий хороший запас по прочности, не очень хочется. Чтобы выяснить, какая может набежать погрешность и в какую сторону и написана данная статья.
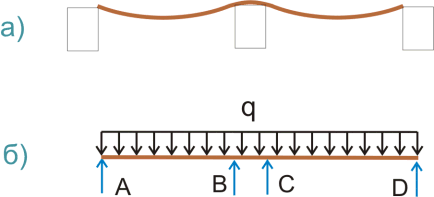
Например, нужно рассчитать на действие равномерно распределенной нагрузки 100 кг/м двухпролетную балку - деревянную лагу шириной b = 5 см, высотой h = 10 см, длиной 2.2 метра с промежуточной опорой - несущей балкой шириной 22 см (подобные размеры выбраны исключительно для упрощения расчетов), расстояние в свету между опорами составляет 0.99 м. Предполагается, что жесткость несущей балки (которую мы дальше будем называть промежуточной опорой) достаточно большая, поэтому влияние осадки опор мы учитывать не будем. Каким образом обеспечивается шарнирное соединение с крайними опорами мы сейчас также решать не будем, сейчас нас интересует промежуточная опора.
Таким образом момент на промежуточной опоре, если принять в качестве расчетного пролета расстояние между опорами в свету, составит:
М = - qlс2/8 = -100·0.992/8 = -12.25125 кгс·м
На неучтенные нами 20 см длины балки под промежуточной опорой вроде бы тоже действует равномерно распределенная нагрузка, но приводя ширину промежуточной опоры к точке, мы эту распределенную нагрузку также сводим к сосредоточенной силе и получается, что на промежуточной опоре просто действует дополнительная сосредоточенная сила, увеличивающая значение опорной реакции. Но так как эти две силы, распределенная нагрузка, приведенная к сосредоточенной силе и опорная реакция, также приведенная к сосредоточенной силе, действуют в одной точке, то для упрощения расчетов влиянием распределенной нагрузки, действующей по ширине опоры, можно пренебречь.
Такое допущение применимо например для рассмотренных выше ребристых перекрытий, однако для балок постоянного сечения следует учесть, что угол поворота поперечных сечений в начале и в конце реальной промежуточной опоры не будет равен нулю, как это принимается при рассмотрении расчетной схемы с опорами - точками. Следовательно и значение момента будет несколько меньше при всех прочих одинаковых параметрах.
Более того, прогиб балки будет равен нулю в начале и в конце промежуточной опоры, а вот посредине промежуточной опоры не будет = 0. И если вспомнить, что мы рассматриваем промежуточную опору, как достаточно жесткую, то нашу балку можно рассчитывать не как двухпролетную, а как трехпролетную, со средним пролетом, равным ширине промежуточной опоры. Потому как балка в результате прогиба будет опираться на грани промежуточной опоры.
Тогда уравнения моментов для такой статически неопределимой балки примут следующий вид:
2MB(l1 + l2) + MCl2 = - 6·Rф1;
MBl2 + 2MC(l2 + l3) = - 6·Rф2; (315.4.1)
где
Rф1 = Rф2 = Aф + Вф = ql13/24 + ql23/24
Теперь осталось определиться с расчетной длиной пролетов. Если бы опорные реакции передавались только в точках В и С, то для расчетов можно было бы использовать l1 = l3 = 1 м и l2 = 0.2 м. Однако абсолютно жестких материалов не существует, да и если бы рассчитываемая балка была бы абсолютно жесткой, то она не прогибалась бы в пролетах. Поэтому опорные реакции будут передаваться не в двух точках, а будут представлять собой нагрузку, неравномерно распределенную по всей ширине промежуточной опоры или на двух участках возле краев промежуточной опоры. Впрочем ничего не мешает найти равнодействующие этих нагрузок, они и будут сосредоточенными силами - опорными реакциями, однако только после того, как будет определен угол наклона поперечного сечения в начале и конце опоры (т.е. только после того, как будет выполнен расчет балки). Больше подробностей здесь.
Причем при малой нагрузке длина опорных участков будет стремиться к минимуму при этом распределение нагрузки будет более равномерным, а при увеличении нагрузки длина опорных участков увеличится, но при этом увеличится и угол наклона, величина прогиба над серединой промежуточной опоры, а значит изменится и распределение нагрузок на опорных участках. Чтобы не вникать в достаточно сложные расчеты, которые мы к тому же пока не можем выполнить, ограничимся тем, что при треугольной эпюре напряжений минимально допустимая длина опорных участков составит:
lo = B / Rсмb = 122.5 / 30·5 = 0.817 см (148.2.2)
где В = 10ql/8 = 100·0.99/8 = 122.5 опорная реакция на промежуточной опоре для двухпролетной балки с пролетами 1 м (примем это значение, так как точное значение опорных реакций для трехпролетной балки пока неизвестно). b - ширина балки, в нашем случае лаги, Rсм - расчетное сопротивление смятию древесины.
Центр тяжести для треугольных эпюр напряжений будет находиться на расстоянии 0.833/3 = 0.278 см. Конечно, для эпюр напряжений, описываемых уравнением прогиба (как минимум кубической параболой), минимально допустимая длина опорных участков будет больше, но и центр тяжести таких эпюр будет ближе к краям промежуточной опоры. Таким образом, если мы примем смещение на 1 см с хорошим запасом, чтобы учесть возможную передачу опорной реакции по всей ширине промежуточной опоры, то длина пролетов составит l1 = l3 = 1 м и l2 = 0.2 м, то
Rф = 100(13 + 0.23)/24 = 4.2
2.4MB + 0.2MC = - 25.2;
0.2MB + 2.4MC = - 25.2;
Так как наша балка является симметричной и приложенная нагрузка является симметричной и соответственно МВ = МС, то мы сразу, без дальнейших долгих и мучительных вычислений можем определить значение моментов:
MB = MС = - 25.2/(2.4 + 0.2) = - 9.692 кгс·м
Разница значений моментов составляет 100(12.25125 - 9.692)/12.25125 = 20.9% или запас по прочности в 1.2 раза.
Посмотрим, к каким погрешностям можно прийти при дальнейших расчетах.
Так для двухпролетной балки значения опорных реакций и моментов уже известны: А = С = 3ql/8 = 37.125 кг, В = 10ql/8 = 122.5 кг, Мпр = 9ql2/128 = 6.89 кгс·м, момент на опоре мы уже приводили. А теперь определим эти же значения для трехпролетной балки
Для определения момента в середине среднего пролета (над промежуточной опорой) определим значения опорных реакций, исходя из следующих условий:
Для первого пролета:
Аl1 - ql12/2 = MB; A = (MB + ql12/2)/l1 = (-9.692 + 100·12/2)/1 = 40.307 кгс
Так как максимальный момент в пролетах будет действовать в сечении, где поперечные силы будут равны 0, то расстояние от начала балки до рассматриваемого сечения составит:
A - qx = 0; x = A/q = 40.307/100= 0.403 м
Максимальный момент в этом сечении будет равен:
M0.3818 = Ax - qx2/2 = 40.3·0.403 - 100·0.42/2 = 8.1235 кгс·м
Для 2 пролета:
A(l1 + l2) + Bl2 - q(l1 + l2)2/2 = MC; B = (MC - A(l1 + l2) + q(l1 + l2)2/2)/l2 = (- 10 - 40.307(1 + 0.2) + 100·1.22/2)/0.2 = 69.694 кгс
тогда максимальное значение момента во втором пролете (над промежуточной опорой) составит
Mmax = 1.1A + 0.1B - q1.12/2 = 1.1·40.307 + 0.1·69.694 - 100·1.12/2 = - 9.193 кгс·м
Для 3 пролета (проверка):
2.2A + 1.2B + С - q(2.2)2/2 = 0; C = (- 2.2A - 1.2B + q(2.1)2/2)/1 = (- 2.2·40.307 - 1.2·69.694 + 100·2.42) = 69.692 кгс
Чтобы убедиться, что расчеты верны нужно проверить, будет ли прогиб равен нулю на опорах. Для этого сначала нужно определить угол поворота на опоре А. Если наши предположения верны, то уравнение прогиба на опоре В будет иметь вид:
fB = tgΘAl1 + Al13/6EI - ql14/24EI = 0;
тогда
tgΘA = ql13/24EI - Аl12/6EI = (100 - 160)/24EI = - 61.228/24EI;
при таком тангенсе угла наклона на опоре А прогиб на опоре С составит:
fС = 1.2tgΘA + A1.23/6EI + B0.23/6EI - q(1.2)4/24EI = (-73.4736 +278.602 + 2.23 - 207.36)/EI = -0.0014/24EI;
прогиб на опоре D составит:
fD = tgΘA3l + A(3l)3/6EI + B(2l)3/6EI +Cl3/6EI - q(3l)4/24EI = (-134.7016 + 1716.7557 + 481.725 + 278.776 - 2342.56)/EI = -0.0049/24EI
Как видим погрешность набегает в третьем знаке после запятой из-за массивности вычислений, потому будем считать наш расчет более менее точным.
Как бы суммарная реакция на промежуточной опоре составит 69.693·2 = 139.386 кгс и тогда разница составит 100(139.386 - 122.5)/122.5 = 13.8%.
Для остальных полученных значений разница меньше, а набежала она из-за того, что при расчетных пролетах, равных расстоянию в свету между опорами, нагрузка, действующая в районе промежуточной опоры не учитывалась. Впрочем если учесть нагрузку действующую на промежуточной опоре, то реакция на промежуточной опоре для двухпролетной балки составит В = 122.5 + 100·0.22 = 144.5 кгс, соответственно разницы почти никакой. А вот разница значений моментов в пролетах набежала 100(8 - 6.89)/6.89 = 16.11%. Поэтому при расчетах по пролетам в свету не нужно забывать о таком увеличении поперечной силы и моментов в пролетах, мало ли чего. Конечно же, чем меньше будет ширина промежуточной опоры, тем меньше будет разница значений, полученных при различных методах расчета, тем не менее промежуточные опоры имеют всегда вполне конкретную ширину. | 
