Например, мы планируем ж/б балку. В крайних пролетах сечение балки 20х20 см, а в среднем пролете, там где у нас действует равномерно распределенная нагрузка, сечение балки будет 40х40 см. Влияние арматуры на общее значение момента инерции мы в данном случае учитывать не будем. Расчетная схема для такой балки будет выглядеть примерно так, как показано на рисунке 487.1.б), вот только жесткости элементов будут другие, а причем тут рама, показанная на рисунке 487.1.а), мы поговорим чуть позже.
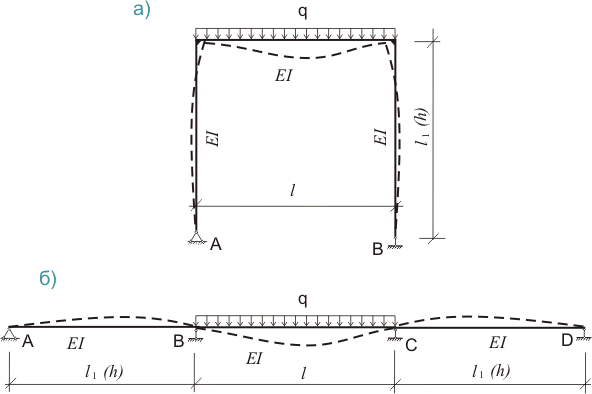
Для начала определим жесткости различных участков балки, точнее соотношение этих жесткостей. Для крайних пролетов:
Iк = bh3/12 = 20·203/12 = 13333.33 см4
Для среднего пролета:
Iс = bh3/12 = 40·403/12 = 213333.33 см4
Теперь нужно выбрать, какой из этих моментов инерции будет основным. Для упрощения расчетов лучше выбрать основным момент инерции для среднего пролета. Тогда
Ic = Io
Io/Iк = 2133333.33/13333.33 = 16
Примечание: вообще-то соотношение моментов инерции можно определить и другим способом. Так как у нас и высота и ширина сечения балки в среднем пролете в 2 раза больше, чем в крайних пролетах, то значение момента инерции в среднем пролете будет больше в 2·23 = 16 раз
Ну а теперь мы можем приступать непосредственно к расчету. Для этого воспользуемся уравнениями трех моментов и в частности формулой (315.5.1):
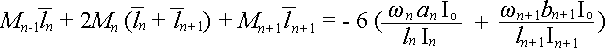
где
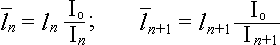
На первый взгляд формула выглядит достаточно сложной, однако при наших условиях составление уравнений трех моментов много времени не займет. Так как у нас три равных по длине пролета, т.е. длина каждого пролета равна l, то:
l1 = lIo/Iк = 16l
l2 = lIo/Ic = l
l3 = lIo/Iк = 16l
Физический смысл приведения длин в том, что балку с равными пролетами и разной жесткостью в пролетах можно рассматривать как балку постоянной жесткости, но с разной длиной пролетов.
Всего нам нужно составить 2 уравнения моментов.
Так как в крайних пролетах балка не нагружена, то и никаких фиктивных опорных реакций при рассмотрении крайних пролетов не будет, а значит и правая часть формулы (315.5.1) упростится. Так как при рассмотрении среднего пролета Io = Ic, то фиктивная опорная реакция для обеих уравнений составит (согласно таблицы 315.1):
Rф = - ql3/24
Теперь у нас есть все данные для составлений уравнений трех моментов:
2MB(16l +l) + MCl = - 6·Rф;
MBl + 2MC(l +16) = - 6·Rф;
Так как при выбранных нами условиях МВ = МС, то нет необходимости решать систему уравнений, достаточно решить одно из них:
34МCl + MCl = - 6ql3/24;
35MCl = - ql3/4;
MC = - ql2/140.
Чтобы определить значение момента в середине среднего пролета, нужно сначала определить опорные реакции, впрочем, при наших условиях задачи это снова будет не сложно:
Для первого пролета:
А16l = MB; A = ( - ql2/140)/16l = - ql/2240
Для 2 пролета:
A(16l + l) + Bl - ql2/2 = MC; B = (17ql2/2240 - ql2/140 + ql2/2)/l = 1121ql/2240
тогда максимальное значение момента в среднем пролете (в середине горизонтального элемента рамы) составит
Mmax = A(16l +0.5l) + B(0.5l) - ql2/8 = - 33l2/4480 +1121l2/4480 - 560ql2/4480 = 528ql2/4480 ≈ ql2/8.5
Общий вывод, который можно сделать из проведенных расчетов, состоит в том, что жесткость среднего элемента балки, в 16 раз превышающая жесткость крайних элементов, приводит к тому, что средняя часть неразрезной балки больше напоминает обычную однопролетную балку на шарнирных опорах, чем часть неразрезной балки.
И чем больше разница жесткостей, тем это подобие больше. Поэтому в случаях, когда жесткость среднего элемента значительно превышает жесткость крайних элементов, то для упрощения расчетов средний элемент можно рассчитывать просто как однопролетную балку на шарнирных опорах, задавшись при этом необходимым коэффициентом надежности.
А теперь несколько слов о раме, показанной на рисунке 487.1. Дело в том, что такую раму можно рассчитывать как трехпролетную неразрезную балку. Более того, рассмотренную выше ситуацию можно отнести к случаю, когда рассматриваются 2 колонны сечением 20х20 см, жестко соединенные с балкой, имеющей сечение 40х40 см. Расчет может быть примерно таким же. Подобная ситуация возникает и в случае, когда нижний и верхний пояс фермы крепятся к колонне и такое соединение можно рассматривать как жесткое в узлах рамы.
Соответственно при расчете рам с большим количеством вертикальных элементов и с горизонтальными элементами, имеющими значительно большую жесткость, чем вертикальные элементы, для упрощения расчетов горизонтальные элементы можно рассматривать как неразрезную балку на шарнирных опорах с соответствующим количеством пролетов.
Примечание: при расчете статически неопределимых конструкций требуется дополнительно выполнять проверку по прогибам, в том смысле, что прогибы на всех опорах должны быть равны нулю. Но в данном случае мы определим прогиб только для опоры С.
Сначала определим угол поворота на опоре А:
fB = tgΘA16l + A(16l)3/6EI = 0;
Так как мы уже перешли к приведенным длинам пролетов балки и рассматриваем как бы балку постоянной жесткости, то и указывать значение момента инерции для каждого из пролетов не нужно. Тогда
tgΘA = - А(16l)2/6EI = 256ql3/(2240·6EI) = 2ql3/105EI;
при таком тангенсе угла наклона на опоре А прогиб на опоре С составит:
fС = 17ltgΘA + A(17l)3/6EI + Bl3/6EI - ql4/24EI = 4352ql4/13440EI - 4913ql4/13440EI + 1121ql4/13440EI - 560ql4/13440EI = 0;
На основании полученных данных можно строить соответствующие эпюры, подбирать сечение арматуры и класс бетона, однако подобный расчет не входит в задачи данной статьи. Примеров подобного расчета на сайте достаточно. | 
