Конечно же, будь моя воля, я бы, перед тем как приводить формулу для определения прогиба изгибаемых элементов с учетом действия поперечных сил, сначала привел бы упрощенную формулу определения прогиба с соответствующим пояснением, что ей можно пользоваться для приблизительного определения прогиба при соотношениях высоты балки к длине h/l < 20.
Тем не менее, к разработке и составлению указанного Свода Правил я никакого отношения не имею, да и вообще до такого уровня просто еще не дорос. А потому считаю, что требования СП следует безусловно выполнять, а как именно это сделать, мы сейчас и узнаем.
Формула для определения прогиба с учетом действия поперечных сил, приведенная в СП, имеет следующий вид:
f = fo[l + c(h/l)2]/k (544.1)
где f0 - значение прогиба, определяемое без учета действия касательных напряжений, т.е. по упрощенной формуле. Формулы для определения прогиба статически определимых балок можно посмотреть здесь. Впрочем для определения прогиба некоторых видов статически неопределимых балок формулы также имеются.
с - коэффициент, учитывающий влияние поперечных сил на прогиб (о том, как определить этот коэффициент, мы поговорим чуть позже).
k - коэффициент, учитывающий возможное изменение высоты сечения по длине балки. При постоянной высоте k = 1.
При этом h - высота поперечного сечения балки, l - длина пролета балки.
Что лично мне не нравится в формуле (544.1)? Только одна маленькая деталь - наличие в квадратных скобках абсолютной величины - длины балки l.
На мой взгляд это делает данную формулу совершенно бессмысленной, так как определяя прогиб f0, измеряемый хоть в метрах хоть в сантиметрах, и умножая его на длину, измеряемую в тех же метрах или сантиметрах, мы получим какую-то абстрактную величину, измеряемую то ли в м2 то ли в см2. Между тем прогиб всегда имеет линейную размерность, т.е. измеряется или в метрах или в сантиметрах.
Полагаю, что это просто опечатка и вместо длины l в формуле должна стоять единица - 1 (действительно 1 и l очень легко спутать). Кроме того, из общих положений теории сопротивления материалов следует, что в общем случае при учете влияния поперечных сил формула для определения прогиба (например, при действии сосредоточенной нагрузки на конце консольной балки) имеет следующий вид:
- fl = Ql3(1 + λ)/3EI (536.13)
где
λ = k(1 + μ)h2/2l2 (536.12)
И тогда коэффициент с это:
с = k(1 + μ)/2 (544.2)
Мне кажется, что это является еще одним подтверждением того, что формула, приведенная в СП, как впрочем и в старом СНиПе, неправильная. А правильный вариант этой формулы должен иметь следующий вид:
f = fo[1 + c(h/l)2]/k (544.1.2)
Тем не менее, как я уже говорил, я не являюсь ни составителем, ни разработчиком указанных нормативных документов, а потому мое мнение - это всего лишь мнение некоего частного лица, учитывать которое не обязательно.
Если у вас получается определить прогиб деревянной балки по приведенной в Своде Правил формуле, то - вперед! Не обращайте на мои сомнения внимания. Ну а для сомневающихся я бы все-таки предложил формулу (544.1.2). Осталось только выяснить, чему же равен коэффициент с.
Древесина не является изотропным материалом. Например значение модуля упругости древесины вдоль и поперек волокон отличается на порядок, чуть ли не на два, и потому для определения значения коэффициента с конечно же следует пользоваться не общими положениями теории сопротивления материалов, а рекомендациями СП.
Так значение коэффициента с следует определять по таблице Е.3 обязательного приложения Е:
Таблица Е.3. Значения коэффициентов k и с для определения прогибов балок с учетом переменности сечений и деформаций сдвига


Тут может возникнуть дополнительный вопрос: а как определить значение коэффициента β, который присутствует чуть ли не во всех формулах данной таблицы?
СП на этот вопрос прямого ответа не дает, однако по контексту таблицы можно догадаться, что
β = h0/h (544.3)
где h - максимальная высота балки (как правило посредине пролета), h0 - высота балки в начале и(или) конце пролета.
Соответственно βh = h0. Так же из приведенной таблицы становится понятным и то, почему при постоянной по всей длине балки высоте сечения, т.е. при β = 1, коэффициент, учитывающий возможное изменение высоты сечения балки, также равен единице - k = 1.
Конечно же в представленной таблице Е.3 представлены далеко не все возможные случаи загружения балок. Как поступать в случаях, когда на балку действуют другие нагрузки, например несимметичные распределенные или сосредоточенные, в СП опять же не объясняется.
Я считаю, что в таких случаях действующие нагрузки следует привести к эквивалентным симметричным равномерно распределенным или сосредоточенным, но это опять же лишь мое личное мнение.
В целом прогиб, определяемый расчетом, должен быть не больше допустимого:
f ≤ fд (544.4)
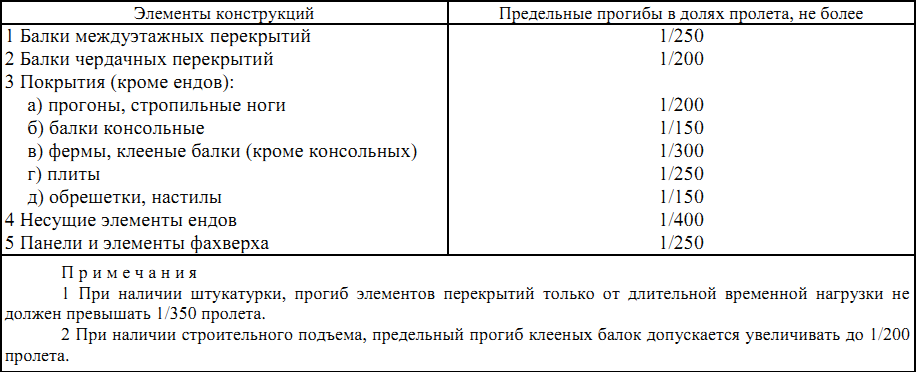
Значение допустимого прогиба определяется по таблице 19:
Таблица 19
Вот собственно и все, что мне хотелось сказать по поводу определения прогиба согласно требований СП 64.13330.2011 "Деревянные конструкции" (Актуализированная редакция СНиП II-25-80). Конкретные примеры определения прогиба деревянных балок приводятся отдельно. | 
