Ранее мы для простоты и наглядности рассматривали обычную деревянную линейку в качестве балки, что позволило с известными допущениями вывести основные уравнения и формулы для расчета несущей способности балки. Благодаря этим уравнениям мы построили эпюры поперечных сил "Q" и эпюры изгибающих моментов "М".
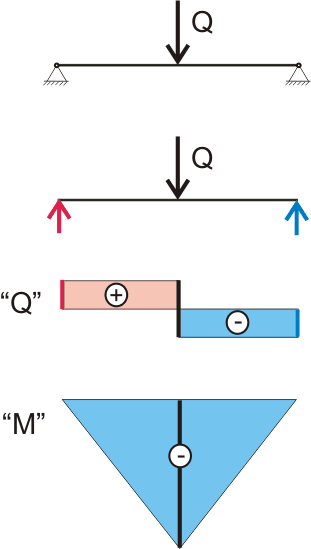
Рисунок 149.2.1. Эпюры поперечных сил и изгибающих моментов, действующих в поперечных сечениях балки при сосредоточенной нагрузке.
Что в итоге позволило достаточно просто и наглядно определить значение максимального изгибающего момента и соответственно значение максимальных нормальных растягивающих и сжимающих напряжений, возникающих в наиболее нагруженном поперечном сечении балки.
Дальше, зная расчетное сопротивление материала балки (значения расчетных сопротивлений проводятся в соответствующих СНиПах), можно достаточно легко определить момент сопротивления поперечного сечения, а затем и другие параметры балки, высоту и ширину, если балка прямоугольного сечения, диаметр, если балка круглого сечения, номер по сортаменту, если балка из металлического горячекатаного профиля.
Такой расчет на прочность является расчетом по первой группе предельных состояний и позволяет определить максимально допустимую нагрузку, которую может выдержать рассчитываемая конструкция. Превышение максимально допустимой нагрузки приведет к разрушению конструкции. Как именно будет разрушаться конструкция, нас в данном случае не интересует, так как данный сайт посвящен не вопросам теоретических и практических исследований предельных состояний материалов, а всего лишь некоторым методам расчетов наиболее распространенных строительных конструкций.
Как правило инженерные расчеты конструкций, которые будут использоваться сотнями тонн и десятками кубометров, выполняются так, чтобы получить максимально загруженную конструкцию. Поэтому такие расчеты достаточно сложные и разного рода коэффициентов, учитывающих срок службы конструкции, характер нагрузок, цикличность, динамичность нагрузок, неоднородность используемого материала и т.д. - десятки. Это логично так как при валовом производстве каждый процент в итоге дает ощутимую экономию. В частном строительстве, выполняемом один раз, прочность конструкции, пусть даже с двукратным запасом намного важнее возможной экономии материалов и потому расчеты для частного малоэтажного строительства можно максимально упростить, используя всего лишь один поправочный коэффициент γ = 1.6÷2, если на этот коэффициент будут умножаться значения напряжений, или γ = 0.5÷0.7, если на этот коэффициент будет умножаться значение расчетного сопротивления. Однако этим даже такие простые расчеты не ограничиваются.
Любая балка, имеющая длину значительно больше, чем высоту поперечного сечения, представляющая собой стержень, под действием нагрузок будет деформироваться. Результатами деформации являются смещение центральной оси балки по оси у относительно оси х, проще говоря прогиб, а также поворот поперечных сечений балки относительно плоскости поперечного сечения. И эти самые прогибы и углы поворота вне зависимости от того, какие опоры у балки и какие на нее действуют нагрузки, также можно определить. Для определения максимального угла поворота и максимального прогиба также строятся соответствующие эпюры, позволяющие определить, какое поперечное сечение сместится в результате прогиба больше всего и какое будет наклонено больше всего.
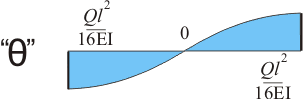
Рисунок 174.5.6. Эпюра углов поворота при действии сосредоточенной нагрузки посредине балки
Эпюра прогибов здесь не приводится, но как ни странно, это самая простая эпюра, показывающая положение оси, проходящей через поперечные сечения балки в результате деформации и эту эпюру воочию можно наблюдать на любой достаточно прогнувшейся балке или любой другой конструкции. Зная модуль упругости материала балки и момент инерции поперечного сечения определить максимальный прогиб также не очень сложно. Максимально упростить решение этих задач позволяют расчетные схемы для балок, к которым в зависимости от характера опор и вида нагружения даны соответствующие формулы.
Такой расчет деформаций является расчетом по предельным состояниям второй группы и достаточно наглядно показывает, на какую величину прогнется балка. Это бывает важно не только в связи с технологическими ограничениями, например для подкрановых балок, но также и из эстетических соображений. Например, когда потолок, а точнее перекрытие, хотя и достаточно прочное, заметно прогнется, то приятного в этом мало. Максимально допустимые величины прогибов для различных строительных конструкций приводятся в СНиП 2.01.07-85 "Нагрузки и воздействия" (в его актуализированной редакции). Впрочем при расчетах для себя никто не запрещает использовать еще меньшие значения прогиба.
Тут у читателя может возникнуть вполне резонный вопрос, а зачем понадобилось строить эпюру касательных напряжений "Q", если ни в каких расчетах эта эпюра не участвует. Что ж, пришло время ответить на этот вопрос.
Дело в том, что расчет разного рода балок, особенно постоянного прямоугольного сечения, лежащих горизонтально, на прочность при действии касательных напряжений очень редко является определяющим в отличие от приведенных выше расчетов. Тем не менее знать, что такое - касательные напряжения - и как они влияют на работу конструкции, пусть даже очень упрощенно, но все-таки надо.
Как следует из определения, касательные напряжения действуют в плоскости поперечного сечения, как бы касаются поперечного сечения потому и названы касательными. Определить значение касательных напряжений на первый взгляд просто: достаточно разделить значение поперечной силы (для этого нам и нужна эпюра "Q"), на площадь поперечного сечения (в рассматриваемом нами примере поперечные силы действовали только вдоль оси у и далее этого нам вполне хватит, усложнить любой расчет мы успеем всегда):
т = Q/F = Q/(bh) (270.1)
В итоге мы можем построить эпюру касательных напряжений "τ"(в дополнение к нормальным напряжениям "σ") следующего вида:

Рисунок 270.1. Предварительная эпюра касательных напряжений "τ"
Однако такая эпюра касательных напряжений была бы справедлива для некоего абстрактного материала, обладающего линейной упругостью вдоль оси у, и абсолютно жесткого вдоль оси z, в результате чего в поперечном сечении такого материала не происходит перераспределения напряжений и есть только один вид деформации относительно оси у. В действительности же любое тело, обладающее изотропными свойствами, под действием нагрузок пытается сохранить свой объем, а значит и рассматриваемое нами сечение пытается сохранить свою площадь. Наглядный пример, когда вы садитесь на мяч, высота его под действием вашего веса уменьшается, но увеличивается ширина. Причем процесс этот носит не линейный характер. Если вырезать из теста кубик или параллелепипед, а затем надавить на него, то боковые грани станут выпуклыми, подобный процесс происходит и при лабораторных испытаниях на сжатие образцов металла или других материалов.
Кроме всего прочего это означает еще и то, что касательные напряжения, действующие вдоль оси у, вызывают появление касательных напряжений вдоль оси z и эпюра касательных напряжений вдоль оси z будет более наглядно показывать изменение касательных напряжений по отношению к высоте балки. При этом форма эпюры будет напоминать боковую грань сплюснутого кубика из теста, а площадь эпюры конечно же не изменится. Т.е. значения эпюры касательных напряжений в самом низу и в самом верху поперечного сечения будут равны нулю, а максимальное значение (при прямоугольном сечении) будет посредине высоты сечения и явно больше Q/F. Исходя из условия равенства площадей эпюр максимальное значение эпюры касательных напряжений не может быть более 2Q/F, да и то только в том случае, если эпюра будет представлять собой два треугольника и в этом случае максимальное значение и есть высота треугольников. Однако как мы уже выяснили эпюра по своему виду больше напоминает часть круга или параболу, т.е. значение максимального касательного напряжения будет составлять около 1.5Q/F:

Рисунок 270.2. Более точная эпюра касательных напряжений.
Серой линией показана предварительно принятая нами эпюра касательных напряжений, но теперь касательные напряжения направлены вдоль оси z.
Математически изменение касательных напряжений в зависимости от высоты сечения можно выразить через изменение статического момента отсеченной части сечения с учетом изменения ширины сечения, так как далеко не всегда балки имеют прямоугольную форму сечения. В итоге формула для определения касательных напряжений (вывод формулы здесь не приводится) имеет следующий вид:
т = QySzотс/bIz (270.2) - формула проф. Д. И. Журавского
где Qy - значение поперечной силы в рассматриваемом поперечном сечении, определяется по эпюре "Q"
Szотс - статический момент отсеченной части сечения на рассматриваемой высоте относительно оси z. Определяется как площадь отсеченной части, умноженная на расстояние между центром тяжести всего сечения и центром тяжести отсеченной части сечения. Например, в самом низу поперечного сечения, т.е. при высоте h=0, площадь отсеченной части сечения будет также равна 0, а значит и касательные напряжения, действующие по ширине b поперечного сечения, также будут равны нулю. Для сечения, проходящего через центр тяжести поперечного сечения, т.е. при высоте отсеченной части сечения, равной h/2, статический момент будет составлять (bh/2)(h/4) = bh2/8. При высоте отсеченного сечения, равной высоте поперечного сечения статический момент будет равен нулю, так как центр тяжести отсеченной части сечения в этом случае будет совпадать с центром тяжести сечения.
b - ширина поперечного сечения на рассматриваемой высоте поперечного сечения. Для балок прямоугольного сечения ширина сечения величина постоянная, однако бывают балки круглого, таврового, двутаврового и любого другого сечения. Более того, определение касательных напряжений чаще всего и используется при расчете балок не прямоугольного сечения, так как при переходе сечения из полок в стенку появляется значительный скачок касательных напряжений в связи с изменением ширины сечения, причем переход из полок в стенку обычно происходит на такой высоте, где нормальные напряжения достаточно велики и это учитывается соответствующим расчетом.
Iz - момент инерции поперечного сечения относительно оси z. В данном случае единственная более менее постоянная величина. Для прямоугольного поперечного сечения момент инерции составляет bh3/12.
Таким образом, согласно формулы (270.2) максимальное значение касательных напряжений для прямоугольного сечения составит:
т = 12Qbh2/(8b2h3) = 1.5Q/F (270.3)
Такой же результат дала нам и геометрия.
И еще. Для материалов, обладающих ярко выраженными анизотропными свойствами, например, для древесины проверка на прочность по касательным напряжениям необходима. Дело в том, что прочность древесины сжатию вдоль волокон и прочность древесины сжатию поперек волокон - абсолютно разные вещи. Поэтому проверка выполняется для поперечных сечений, в которых касательные напряжения максимальны, как правило это сечения на опорах балки (при равномерно распределенной нагрузке). В этом случае полученное значение касательных напряжений сравнивается со значением расчетного сопротивления древесины сжатию или смятию поперек волокон - Rc90.
Впрочем, существует и другой подход к вопросу определения касательных напряжений: под действием нагрузок балка деформируется, при этом максимальные нормальные сжимающие и растягивающие напряжения возникают в самом низу и в самом верху поперечного сечения балки, что можно видеть по эпюре "σ" на рис.270.1.
При этом между волокнами такого неоднородного материала, как древесина, как впрочем и между слоями любого другого материала возникают касательные напряжения, направленные теперь по оси х, т.е. по той же оси, что и нормальные сжимающие и касательные напряжения, возникающие в результате действия изгибающего момента.
Происходит это от того, что каждый рассматриваемый слой испытывает разные по значению нормальные нагрузки и в результате все того же перераспределения напряжений и возникают касательные напряжения. Эти касательные напряжения как бы пытаются расколоть балку на отдельные слои, каждый из которых будет работать как отдельная балка.
Разница же несущей способности между отдельно взятыми слоями и цельной балкой очевидна. Например, если взять пачку бумаги хоть в 500 листов, то согнуть такую пачку - пара пустяков, а если склеить все листы, т.е. слои балки между собой, то мы получим цельную балку и вот ее уже согнуть будет намного труднее. Но между склеенными листами и будут возникать те самые, условно говоря, нормальные касательные напряжения. Впрочем, значение нормальных касательных напряжений определяется таким же образом и в расчетах участвует все та же поперечная сила, определяемая по эпюре "Q". Вот только рассматривается не отсеченная, а скалываемая часть сечения, соответственно статический момент может обозначаться - Szск. В этом случае полученное значение касательных напряжений сравнивается со значением расчетного сопротивления древесины сколу вдоль волокон - Rcк.
Правда, значения Rс90 и Rcк для древесины имеют одинаковое значение, но тем не менее касательные напряжения от действия поперечных сил и от деформаций в результате прогиба принято различать (так как рассматриваются две перрпендикулярные друг другу главные площадки напряжений), да и направление действия касательных напряжений важно при определении общего напряжения в исследуемой точке тела.
Впрочем, все это не более чем общие понятия о касательных напряжениях. В реальных материалах процесс перераспределения напряжений намного более сложный, все потому, что даже металл отнести к изотропным материалам можно достаточно условно. Впрочем эти вопросы рассматривает отдельная научная дисциплина - теория упругости. При расчете строительных конструкций, представляющих собой стержни - балки или пластины - плиты размером на помещение, вполне можно пользоваться формулой (270.2), выведенной на основе общих положений линейной теории упругости. При расчете массивных тел следует использовать методы нелинейной теории упругости. |

