Для примера примем длину галереи - 6.2 метров, а ширину 6 метров - это и будет пролет ферм. Впрочем и ширина и длина такой галереи будет ограничена только размерами участка и вашими финансовыми возможностями. Место строительства - дача в Подмосковье.
Вот в общем-то и все необходимые исходные данные. Казалось бы, не много, но давайте посмотрим, что из этого может получиться.
Перед тем как начинать расчет, следует определиться с геометрическими параметрами фермы, дело в том что геометрия арочных ферм достаточно разнообразна.
Варианты арочных ферм

Рисунок 290.1. Варианты конструкций арочных ферм
а) - арочная ферма с радиусами окружности поясов, равными половине расстояния между началом и концом пояса - диаметра окружности;
б) - арочная ферма с равными расстояниями между верхним и нижним поясом (как бы часть фермы, изображенной на рисунке 290.1.а);
в) - арочная ферма с одинаковым радиусом верхнего и нижнего пояса;
г) - арочная ферма радиус, у которой радиус окружности нижнего пояса больше радиуса окружности верхнего пояса;
д) - ферма с верхним арочным поясом;
е) - ферма с нижним арочным поясом.
На рисунке 290.1 представлены некоторые возможные варианты для арочных ферм, один или два пояса которых описываются уравнением окружности, но центральная ось поясов может описываться и уравнением параболы. Кроме того стержни верхнего и нижнего поясов могут быть прямолинейными, при этом арка состоит как бы из ломанных линий, да и опоры могут быть в самых разных местах, не только в крайних узлах фермы, так что вариантов конструкции арочных ферм существует очень много. Какой из представленных выше вариантов нравится вам больше, я не знаю, а чтобы никому не было обидно дальнейший расчет будет производиться для фермы, представленной на рисунке 290.1.в).
1 этап. Определение геометрических параметров фермы
Пока предполагается, что фермы будут располагаться с шагом 1.05 м, а нагрузка на ферму от обрешетки будет передаваться только в узлах фермы. Кровельным материалом будет служить сотовый поликарбонат со стандартными размерами листа 2.1х6 или 2.1х12 метров (в связи с такой шириной листов и принят шаг ферм).
Высота фермы может быть теоретически любой в пределах 3 м. Дальнейший расчет будет произведен для фермы высотой около 1.5 м. Такая высота принята из эстетических соображений, совмещенных с соображениями экономии. Так как перекрыть ферму одним листом длиной 6 м все равно не получится, то высоту фермы можно подобрать из соображений использования 1 листа длиной до 12 м. В этом случае нужно сначала определиться с расстояниями между верхним и нижним поясами, да и вообще с основными геометрическими параметрами арочной фермы. Большим подспорьем в этом будет любая графическая программа, позволяющая не просто рисовать векторные рисунки, но и определять размеры нарисованных объектов. Например, даже без точных расчетов можно принять следующие параметры, определенные графически:

Рисунок 290.2. Определение геометрических параметров арочной фермы графическим методом.
Как видно из рисунка 305.2, при пролете между опорами l = 6.0 м и при стреле нижней арки f = 1.3 м, радиус окружности, описывающей нижний пояс фермы будет составлять r = 4.1 м. Конечно, графический метод не является точным методом, законы геометрии, выраженные в математической форме, позволяют определить значение радиуса намного точнее. Более подробно закономерности, на которых строится расчет, приводятся в другой статье, а здесь лишь отмечу, что точное значение радиуса составит r = 4.115 м, а значение угла между радиусами α = 105.9776о. Вообще-то, когда я определял графическим способом радиус арки, то значение было тоже не 4.1, а немного больше, я его просто округлил до более удобного, но даже при этом разница составляет не более 0.25%, на что с учетом технологии изготовления поясов фермы можно не обращать внимания.
Примечание: все то же самое можно сделать и, так сказать, аналоговым методом, т.е. просто нарисовать все это на бумаге.
Также графическим способом было определено расстояние между крайними узлами фермы l = 6.5 м (показано на рисунке 305.2 темно-зеленым цветом). При расстоянии между стержнями верхнего и нижнего пояса, принятом h = 0.55 м стрела арки верхнего пояса составляет f = 1.62 м. А вот определить длину верхнего и нижнего пояса проще всего все-таки математически. Длина нижнего пояса будет равна длине дуги окружности и составит
mн = ПRa/180 = 3.141·4.115·93.7147/180 = 6.73 м, (278.1.4)
Длина верхнего пояса составит
mв = ПRa/180 = 3.141·4.115·105.9776/180 = 7.61 м, (278.1.4)
Длина стержней нижнего пояса составит
lс.н. = 6.73/12 = 0.5608 м
а расстояние между узлами нижнего пояса около 55.1 см, за исключением крайних участков фермы.
Примечание: в данном случае расстояние между верхним и нижним поясами посредине фермы принято 55 см не только из эстетических соображений, но и с учетом того, что покрытием будет служить сотовый поликарбонат, а значит расстояние между узлами верхнего пояса фермы, т.е. между балками обрешетки не должно быть большим. Тем не менее никто не запрещает принимать большее или меньшее значение расстояния между верхним и нижним поясами. Например, верхний пояс можно разбить на 8 или на 16 пролетов. При 8 пролетах длина стержней верхнего пояса будет составлять 95.1 см и в этом случае расстояние между верхним и нижним поясами из эстетических соображений следовало бы принять 87-90 см. При 16 пролетах длина стержней верхнего пояса составит 47.56 см и тогда расстояние между верхним и нижним поясом может составлять 40-45 см.
В принципе для ряда дальнейших расчетов можно использовать приведенные выше данные. Однако при расчете стержней фермы потребуются более точные значения. Примем расстояние по вертикали от крайнего узла нижнего пояса до крайнего узла верхнего пояса равным 0.25 м. Для определения более точного значения стрелы верхней арки необходимо сначала решить несколько уравнений. Так как
f = (L/2)tg(α/4) = R(1 - cos(α/2) (290.1.1)
то подставив известные значения L = 6.5 м, R = 4.115 м и выполнив необходимые преобразования, получим
0.78979tg(α/4) + cos(α/2) = 1 (290.1.2)
Решение уравнения (290.1.2) даст нам значение угла между крайними узлами верхнего пояса αв = 104.34о, тогда более точное значение стрелы верхней арки fв = (6.5/2)tg(104.34/4) = 1.5911 м.
Уточненная расчетная схема фермы будет выглядеть так:
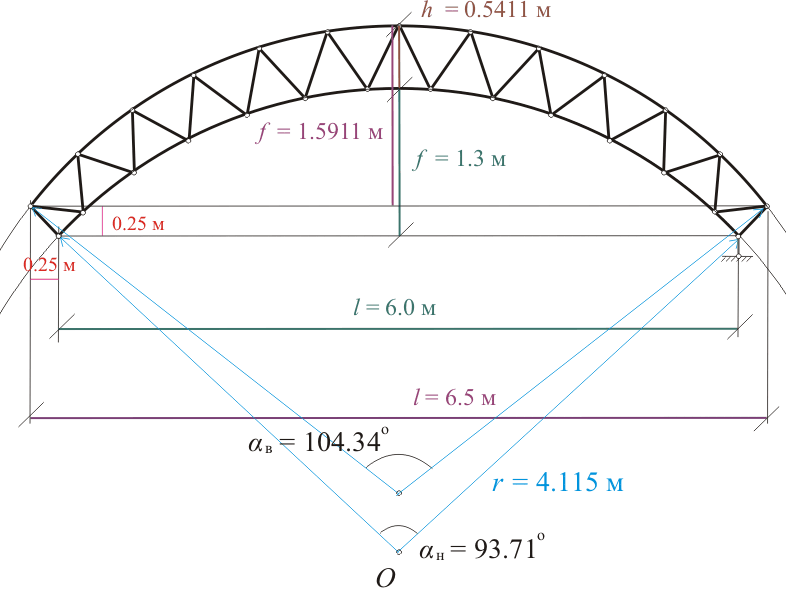
Рисунок 290.3. Уточненная расчетная схема арочной фермы.
Более точное значение длины верхнего пояса составит
mв = ПRa/180 = 3.141·4.115·104.34/180 = 7.494 м, (278.1.4)
Таким образом длину листов поликарбоната можно принимать равной 7.6 м (с учетом большего радиуса покрытия, а также небольшого свеса по краям фермы), при этом длина стержней верхнего пояса составит
lс.в. = 7.494/12 = 0.6247 м
В итоге расчетная схема для арочной галереи будет выглядеть так:
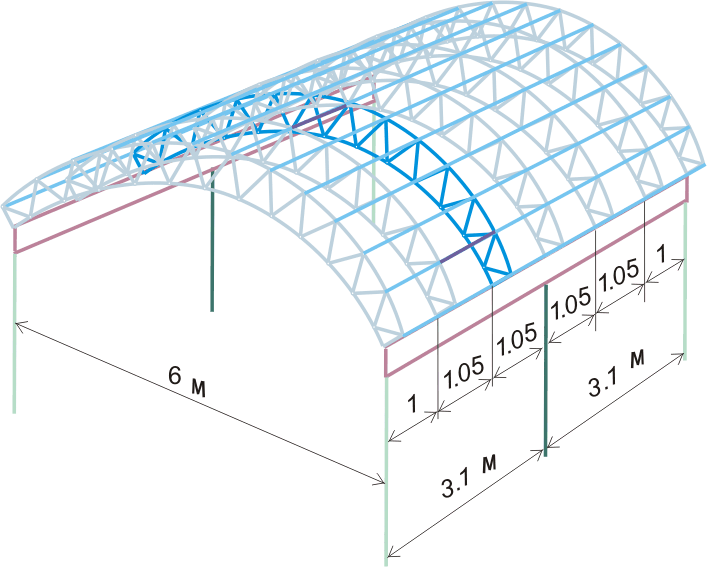
Рисунок 290.4. Расчетная схема арочной галереи
Теперь, когда мы определились с геометрическими параметрами фермы, можно приступать к расчету сотового поликарбоната. Впрочем, следует понимать, что весь расчет выполняется по законам теоретической механии и теории сопротивления материалов и потому без понимания основ этих наук дальнейшее чтение большого смысла не имеет. | 
