Расчет многопролетной балки методом моментов

Многопролетные балки даже в частных малоэтажных домах не такая уж и редкость. Так любую половую доску, укладываемую на лаги, или лист гипсокартона, подшиваемый к профилям потолка, можно рассматривать как многопролетную неразрезную балку. Впрочем и половые доски и гипсокартонные листы в расчете как правило не нуждаются, а вот монолитное железобетонное перекрытие по балкам рассчитывать нужно.

Вот только сделать это не так уж и просто, потому как многопролетные неразрезные балки являются статически неопределимыми конструкциями и потому при расчетах следует использовать или метод сил или метод опорных моментов. При большом количестве пролетов лучше использовать метод моментов. Например:

Пример расчета железобетонной плиты перекрытия по балкам

Планируется перекрытие по балкам в помещении размерами 5х8 метров. Если использовать 4 балки - дополнительные опоры, то плита будет представлять собой 5 пролетную балку. При этом шаг между балками можно выбирать, руководствуясь эстетическими соображениями, т.е. принять одинаковый шаг для всех балок. А если потолки в последствии будут зашиваться, то шаг балок лучше выбирать из конструктивных соображений. Дальнейший расчет будет произведен для балок, расположенных с одинаковым шагом. Расчет параметров таких балок приводится отдельно.

Рассмотрим следующую расчетную схему:

Рисунок 313.1

Монолитная плита по балкам, показанная на рис. 313.1 а), представляет собой 5 пролетную неразрезную балку, на которую будет действовать как минимум два вида нагрузок: постоянная и временные. Как правило к постоянной нагрузке относится собственный вес конструкции, а вес стяжки и напольного покрытия относятся к временной нагрузке. При расчете однопролетных балок это принципиального значения не имеет, так как учитываются все действующие нагрузки. При расчете же многопролетных балок следует учитывать возможные максимально неблагоприятные сочетания нагрузок. Варианты приложения таких нагрузок показаны на рис. 313.1. г) и д). Потому для упрощения расчетов с использованием указанных расчетных схем, вес стяжки и напольного покрытия можно отнести к постоянной нагрузке.

Таким образом расчетное значение постоянной нагрузки составит:

q_п = (0.08·1 + 0.11·0.17/1.62)2500·1.1 + 200 = 251.7 +200 = 451.7 кг/м

где γ_н = 1.1 - коэффициент надежности по нагрузке.

Значение нормативной временной нагрузки на перекрытие определяется по СНиП 2.01.07-85 "Нагрузки и воздействия", и составляет 150 кг/м². Тогда с учетом коэффициента надежности по нагрузке, при таком значении нормативной нагрузки составляющем γ_н = 1.3 (1.4 по старым нормам), расчетное значение временной нагрузки составит

q_в = 150·1·1.3 = 195 ≈ 200 кг/м

Примечание: Устройство перегородок, установка тяжелого инженерного оборудования и другие дополнительные значительные нагрузки данным расчетом не предусматриваются.

Теперь, когда действующие нагрузки определены, осталось только рассчитать плиту:

1. Расчет на действие постоянной нагрузки

Расчетная схема для данного расчета представлена на рис. 313.1 б). Так как нагрузка во всех пролетах одинаковая, длина пролетов одинаковая и жесткость балки во всех пролетах одинаковая, то система уравнений трех моментов значительно упростится и будет иметь следующий вид:

2M_B(2l) + M_Cl = - 6·86.0542l;

M_Bl + 2M_C(2l) + M_Dl = - 6·86.0542l;

            M_Cl + 2M_D(2l) + M_El = - 6·86.0542l; (316.1)

M_Dl + 2M_E(2l) = - 6·86.0542l;

где

R^ф₁ = R^ф₂ = R^ф₃ = R^ф₄ = A^ф + В^ф = 2ql³/24 = 451.7·1.512²·l/12 = 86.0542l

тогда

4M_B + M_C = - 516.3256;

M_B + 4M_C + M_D = - 516.3256;

M_C + 4M_D + M_E = - 516.3256;

M_D + 4M_E = - 516.3256;

Принимаем а_B = 1, тогда согласно формул (315.4):

а_C = - 2(1 + 1) = -4;

a_D = - 2(1 + 1)a₂ - a₁ = 15

a_E = - 2(1 + 1)a₃ - a₂ = -56

тогда

М_Е = - 516.3256l(a_B + a_C +a_D +a_E)/(l(a_D + 4a_E) = - 516.3256(1 - 4 + 15 - 56)/(15 - 4·56) = - 22718.327/209 = - 108.7 кгс·м (ql²/9.5)

Подставляя полученное значение в последнее уравнение системы (316.1) получим следующее значение момента:

M_D = 4·108.7 - 516.3256 = - 81.5256 кгс·м (ql²/12.67)

Так как наша балка является симметричной и приложенная нагрузка является симметричной, то значение момента на опоре С должно быть равно значению момента на опоре D, а значение момента на опоре В должно быть равно значению момента на опоре Е. Проверяем:

M_С = 4·81.5256 + 108.7 - 516.32 = - 81.5232 кгс·м

M_В = (81.5232 - 516.32)/4 = - 108.7 кгс·м 

Так как значения сошлись (небольшие расхождения не учитываем), то дальнейшую проверку в принципе можно не выполнять. Для определения моментов в пролетах определим значения опорных реакций, исходя из следующих условий:

Для первого и последнего (1 и 5) пролетов:

Аl - ql²/2 = Fl - ql²/2 = M_B = M_E A = F = (M_B + ql²/2)l = (-108.7 + 451.7·1.512²/2)1.512 = 269.5936 кгс

Так как максимальный момент в пролетах будет действовать в сечении, где поперечные силы будут равны 0, то расстояние от начала балки до рассматриваемого сечения составит:

A - qx = 0; x = A/q = 269.5936/451.7 = 0.5968 м (0.3947l)

Максимальный момент в этом сечении будет равен:

M_1,5 = Ax - qx²/2 = 269.59·0.5968 - 451.7·0.5968²/2 = 80.45 кгс·м (ql²/12.835)

Момент посредине 1 и 5 пролета будет равен:

M_1,5(l/2) = Al/2 - q(l/2)²/2 = 269.59·1.512/2 - 451.7·(1.515/2)²/2 = 74.73 кгс·м (ql²/13.82)

Для 2 и 4 пролетов:

2Al + Bl - q(2l)²/2 = M_C; B = Е = (M_C - 2Al + q(2l)²/2)l = ( - 81.52 - 2·269.59·1.512 + 451.7· 4.5723)/1.512 = 772.845 кгс

А + В - qx = 0; x = (A + B)/q = (269.59 + 772.845)/451.7 = 2.3078 м (или 2.3078 - 1.512 = 0.7958 м (0.526l) от опоры В)

M_2,4 = Ax + B(x - l) - qx²/2 = 269.59·2.3078 + 772.845·0,7958 - 451.7·2.3078²/2 = 34.326 кгс·м (ql²/30.1)

Для 3 пролета:

3Al + 2Bl +Сl - q(3l)²/2 = M_D; C = (M_D - 3Al - 2Bl + q(3l)²/2)l = ( - 81.52 - 3·269.59·1.512 - 2·772.845·1.512 + 451.7· 10.2876)/1.512 = 665 кгс

А + В +C - qx = 0; x = (A + B + C)/q = (269.59 + 772.845 + 665)/451.7 = 3.78 м (или 3.78 - 2·1.512 = 0.756 м (l/2) от опоры С)

M₃ = Ax + B(x - l) + C(x - 2l) - qx²/2 = 269.59·3.78 + 772.845·2,268 + 665·0.756 - 451.7·3.78²/2 = 47.57 кгс·м (ql²/21.71)

На основании этих данных мы можем построить эпюру моментов для плиты:

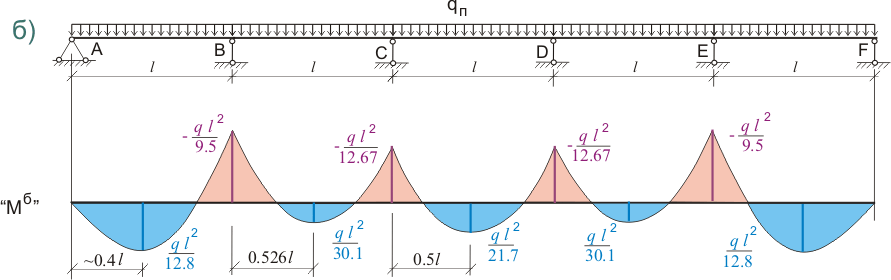
Рисунок 316.1

2. Проверка по деформациям

Если мы правильно определили значения моментов и опорных реакций, то прогибы на промежуточных опорах должны быть равны 0. Проверим прогиб на опоре В. Для основной балки с опорами А и В угол поворота на опоре А равен фиктивной опорной реакции, деленной на жесткость, для вспомогательной балки с опорами А и В, угол поворота на опоре А зависит от значения момента на опоре В, тогда:

EIΘ_А = - ql³/24 + ql³/(6·9.5) = - 33ql³/1368 = - ql³/41.45

тогда прогиб на опоре В составит:

EIf_B = Θ_Al + Al³/6 - ql⁴/24 = - 451.7·33·1.512⁴/1368 + 269.5936·1.512³/6 - 451.7·1.512⁴/24 = - 56.948868 + 155.31514 - 98.36622 = 0.00005 ≈ 0

В данном случае, как и в предыдущем, небольшая погрешность набежала из-за того, что при расчетах мы использовали округленные данные.

Примечание: если есть сомнения в правильности расчетов, то следует проверить прогибы на всех опорах.

3. Расчет на действие временной нагрузки, действующей по всей длине плиты

Так как временная нагрузка при варианте загружения, показанном на рис. 313.1. в) будет действовать по всей длине плиты, то для определения моментов в пролетах и на опорах достаточно умножить значения, полученные при расчетах на действие постоянной нагрузки на отношение временной нагрузки к постоянной:

k = q_в/q_п = 200/451.7 = 0.44277 ≈ 0.443

Таким образом суммарные моменты на опорах и в пролетах при действии постоянной и временной равномерно распределенных нагрузок, действующих по всей длине балки, будут составлять:

М^б+в = М^б(1 + k) = 1.443М^б

Тогда

М^б+в_В = М^б+в_Е = - 108.7·1.443 = - 156.85 кгс·м

М^б+в_С = М^б+в_D = - 81.53·1.443 = - 117.65 кгс·м

М^б+в₁ = М^б+в₅ = 80.45·1.443 = 116.1 кгс·м

М^б+в_1(l/2) = М^б+в_5(l/2) = 74.73·1.443 = 107.83 кгс·м

М^б+в₂ = М^б+в₄ = 34.33·1.443 = 45.54 кгс·м

М^б+в₃ = 47.57·1.443 = 68.64 кгс·м

Эпюра моментов при действии временной нагрузки по схеме в) ничем не будет отличаться от эпюры, показанной на рис. 316.1. Суммарная эпюра от действия постоянной нагрузки и временной по схеме в) будет иметь такой же вид, изменятся только значения моментов. А если временная нагрузка будет приложена так, как показано на схеме г) или д), то суммарная эпюра изменит свой вид, но сначала следует определить значения моментов.

4. Расчет на действие временной нагрузки, действующей по схеме г)

При выбранной схеме загружения изменится сумма фиктивных опорных реакций. Так как нагрузка будет действовать через пролет, то сумма фиктивных опорных реакций уменьшится в 2 раза и составит:

R^ф₁ = R^ф₂ = R^ф₃ = R^ф₄ = A^ф + 0 или 0 + В^ф = ql³/24 = 200·1.512²·l/24 = 19.0512l

Если мы разделим это значение, на значение фиктивной опорной реакции при действии постоянной нагрузки, то получим:

19.0512l/86.0542l = 0.22138 = k/2

Это позволяет не решать еще раз систему уравнений, а сразу определить значения моментов на опорах при временной нагрузке по схеме г)

М^г_В = М^г_Е = - 108.7·0.22138 = - 24.064 кгс·м

М^г_С = М^г_D = - 81.53·0.22138 = - 18.049 кгс·м

М^г₁ = М^г₅ = 80.45·0.22138 = 17.81 кгс·м

Так как во 2 и 4 пролетах временная нагрузка отсутствует, то момент в этих пролетах будет отрицательным и значение момента посредине пролета будет равно:

М^г_2(l/2) = М^г_4(l/2) = (М_В + М_С)/2 = - (24.064 + 18.049)/2 = - 21.06 кгс·м

М^г₃ = 47.57·0.22138 = 10.53 кгс·м

5. Расчет на действие временной нагрузки, действующей по схеме д)

Как ни странно, но при схеме загружения д) сумма фиктивных реакций не изменится, а значит и не изменятся значения моментов на опорах, а изменятся только значения моментов в пролетах:

М^д_1(l/2) = М^д_5(l/2) = М_В/2 = - 24.064/2 = - 12.032 кгс·м

М^д₂ = М^д₄ = 34.33·0.22138 = 7.6 кгс·м

М^д₃ = М_С = М_D = - 18.049 кгс·м

6. Построение огибающей эпюры моментов

На основании полученных данных мы можем построить так называемую "огибающую" эпюру моментов, т.е. такую эпюру, на которой будут учтены значения моментов в пролетах при временной нагрузке по схемам г) и д). Другими словами мы на основную эпюру "М^б+в" наложим эпюры "М^б+г" и "М^б+д". Огибающая эпюра нужна нам для того, чтобы определить пределы, в которых изгибающий момент будет вызывать растяжение верхней зоны сечения плиты.

Дополнительных данных будет не так уж и много

М^б+д_1(l/2) = 74.73 - 12.032 = 62.7 кгс·м

М^б+г₂ = 34.326 - 21.06 = 13.266 кгс·м

М^б+д₃ = 47.47 - 18.049 = 29.52 кгс·м

М^б+г_В = М^б+д_В = - 108.7 - 24.064 = - 132.76 кгс·м

М^б+г_С = М^б+д_С = - 81.53 - 18.049 = - 99.58 кгс·м

Огибающая эпюра для выбранных расчетных схем будет выглядеть так:

Рисунок 316.2

Теперь, когда максимальные значения моментов на опорах и в пролетах определены, подобрать требуемую арматуру для всех пролетов не сложно.

Например, для первого пролета на приопорном участке потребуется армирование при h₀ = 6 см и при R_b = 117·0.9 = 105.3 кг/см²:

a_m = 156.9/(1·0.06²·1053000) = 0.0414

A_s = 105.3·100·6(1 - √‾(1 - 2·0.0414)) / 3600 = 0.742 см².

Получается, что даже для самого нагруженного участка плиты шириной 1 м достаточно 4 стерженей d = 5 мм с площадью 0.79 см². При этом коэффициент армирования получается:

μ% = 100·0.79/100·6 = 0.13 %

что в 2-4 раза меньше рекомендуемого. С учетом того, что в остальных пролетах и на остальных опорах момент меньше, мы можем уменьшить высоту плиты. Согласно СНиП 2.01.03-84 п.5.3 толщина плит междуэтажных перекрытий в жилых зданиях должна быть не менее 5 см. Согласно п.5.5 высота защитного слоя при высоте конструкции до 100 мм - не менее 10 мм и не менее диаметра арматуры. Исходя из этих требований мы можем принять высоту плиты 6 см, а расстояние а = 1.5 см, что обеспечит высоту защитного слоя 10 мм даже при диаметре арматуры 10 мм. Тогда при h_o = 4.5 см

a_m = 156.9/(1·0.045²·1053000) = 0.0736

A_s = 105.3·100·4.5(1 - √‾(1 - 2·0.0736)) / 3600 = 1.007 см².

Тогда для армирования приопорных участка (опоры В и Е) достаточно 4 стерженей d = 6 мм с площадью 1.13 см², для надежности можно принять 5 стержней диаметром 6 мм и высоту h_o = 4.7 см.

Такое уменьшение высоты плиты приведет к ощутимому изменению значения постоянной нагрузки, но также и к изменению параметров тавровой балки. Поэтому и плита и балки при таком изменении параметров нуждаются в перерасчете.

Уточненное расчетное значение постоянной нагрузки составит:

q_п = (0.06·1 + 0.11·0.24/1.62)2500·1.1 + 200 = 210+200 = 410 кг/м

Значение временной нагрузки оставляем без изменения. Тогда при соотношении нагрузок 410/451.7 = 0.91 значение расчетных моментов при максимальной нагрузке составит:

М^б+в_В = М^б+в_Е = - 156.85·0.91 = - 142.34 кгс·м

М^б+в_С = М^б+в_D = - 117.65·0.91 = - 106.8 кгс·м

М^б+в₁ = М^б+в₅ = 116.1·0.91 = 105.4 кгс·м

М^б+в_1(l/2) = М^б+в_5(l/2) = 107.83·0.91 = 97.9 кгс·м

М^б+в₂ = М^б+в₄ = 45.54·0.91 = 41.3 кгс·м

М^б+в₃ = 68.64·0.91 = 62.3 кгс·м

Уточненная огибающая эпюра моментов будет выглядеть так:

Рисунок 316.3

Примечание: Следует учитывать, что в чистом виде эти данные можно применить только для первого и последнего метров плиты. Так как железобетонные балки, на которые опирается плита, в отличие от стен - опор А и F, будут прогибаться и чем ближе к середине, тем больше прогиб будет стремиться к максимальному. Такой прогиб будет приводить к перераспределению моментов. Для приближенных расчетов можно уменьшить значение моментов на опорах В и Е на 10% и на столько же увеличить значение моментов в 1 и 5 пролете. Более точный учет влияния проседающих опор - отдельная история.

Согласно Пособия по проектированию "Армирование элементов монолитных железобетонных зданий" 2007 года издания толщину балочных плит в перекрытиях жилых и общественных зданий с отношением сторон l₂/l₁ >2 следует принимать не менее 70 мм, а защитный слой бетона - не менее 20 мм. В целом это очень правильное требование, однако оно не предусматривает возможную разницу в длине пролетов, а шаг ребер -  балок 1.6 м является довольно частным. Тем не менее при использовании для бетонной смеси щебня с крупностью зерен более 30 мм это требование следует выполнять.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

На главную

• Расчет конструкций ::: Статически неопределимые конструкции
• Расчет конструкций ::: Расчет железобетонных конструкций

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).