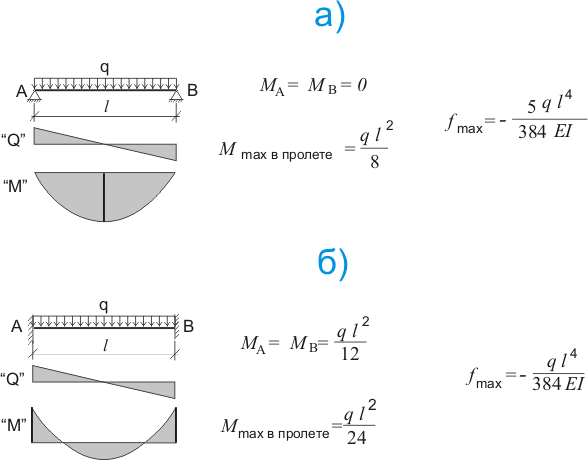
Рисунок 219.1. Зависимость значений изгибающих моментов и прогибов от варианта опирания балки.
На рисунке 219.1.а показана балка с шарнирными опорами. Для такой балки максимальный изгибающий момент М и соответственно максимальные нормальные напряжения будут действовать в поперечном сечении, расположенном посредине пролета, при этом момент на опорах будет равен 0. На рисунке 1.б показана балка, имеющая такой же пролет и к балке приложена такая же нагрузка, как и к балке на рисунке 219.1.а. При этом для балки, изображенной на рисунке 219.1.б максимальные изгибающие моменты будут действовать на сечения, находящиеся на опорах, их значение будет в 1.5 раза меньше, чем для балки на шарнирных опорах, а максимальный прогиб f будет в 5 раз меньше.
Как видим разница ощутимая. А для железобетонных конструкций определение растянутых и сжатых областей особенно важно, так как железобетон это комплексный материал, в котором бетон, как искусственный камень, работает на сжимающие напряжения, а металлическая арматура устанавливается как правило в растягиваемой области, что позволяет не учитывать гибкость стержней и тем самым использовать прочностные свойства металла максимально. Таким образом правильное определение вида опор позволит сэкономить порядочное количество материала. Кроме того, так как любая балка, например, перемычка или плита перекрытия имеет определенные участки, предназначенные для опирания, то такую балку можно рассматривать как двухконсольную балку с двумя шарнирными опорами у которой опорные участки - это консоли балки, правда при относительно небольших размерах таких участков большого смысла в этом нет.
Если Вы не знаете, какое опирание будет у Вашей конструкции, то принимайте шарнирное бесконсольное. Самое худшее, что при этом может случиться, это запас конструкции по прочности в 1.5-2 раза
Тем же, кто надеется немного сэкономить на изготовлении конструкции, придется читать статью до конца. Ну а теперь о главном: почему в строительной механике и сопромате используются такие понятия, как шарнирные опоры и жесткое защемление на опорах и как с этим жить?
В большинстве случаев расчет строительной конструкции является упрощенным и приближенным, это позволяет выполнить расчет максимально быстро и просто. Например, нужно рассчитать перемычку из прокатного профиля, которая будет укладываться на раствор, используемый при возведении кирпичной стены. Чтобы выполнить расчет максимально точно, нужно кроме нагрузки, действующей на перемычку, также знать не только длину пролета, но и полную длину перемычки с учетом опорных частей, прочность кладочного раствора и прочность кирпича на сжатие, геометрическую форму кирпичей, силу сцепления металла с раствором и силу трения между металлом и раствором, возможные дефекты кладочного раствора, прокатного профиля, прямолинейность профиля, разность отметок опорных площадок и много чего еще. Однако строительная механика, если принять для перемычки шарнирное опирание без консолей, позволяет упростить расчет до минимума при использовании следующих допусков и расчетных предпосылок:
1. Перемычка рассматривается как однородное тело, обладающее изотропными свойствами, т.е. одинаковыми физико-механическими свойствами во всех направлениях. Это позволяет рассматривать перемычку как абсолютно плоский прямолинейный стержень лежащий на оси х. Ось х проходит через центр тяжести поперечных сечений стержня. Нагрузка приложена по оси у, т.е. попадает на ось х, проходящую через центры тяжести поперечных сечений.
2. Так как стержень абсолютно плоский, то опорные участки перемычки сводятся к двум опорным точкам А и В, при этом внутренние напряжения действующие на опорные участки по оси у сводятся к сосредоточенным нагрузкам, которые в данном случае представляют собой опорные реакции. Так как опорные площадки и опорные участки балки сведены к точкам, то и сосредоточенные опорные реакции прикладываются в опорных точках. Таким образом при расчетах используется не полная длина перемычки, а пролет балки l - расстояние между опорными точками.
3. Сила действия равна силе противодействия, например, общая нагрузка, действующая на перемычку равна сумме опорных реакций.
4. Сила сцепления металла с раствором и сила трения, возникающая при перемещении балки по оси х, принимаются достаточными для обеспечения неподвижности балки по этой оси в опорной точке А и не учитываются для опорной точки В. Другими словами в точке А балка смещаться по оси х не может, а в точке В может свободно.
5. Так как перемычка под действием нагрузки будет прогибаться, то на расчетной схеме нужно как-то обозначить расстояние между землей и перемычкой.
Наиболее полно данным расчетным предпосылкам отвечает следующая расчетная схема:
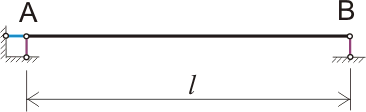
Рисунок 219.2. Шарнирно опертая безконсольная балка.
Суть данной расчетной схемы следующая: наша перемычка представляет собой стержень, который шарнирно соединен с тремя условными опорными стержнями, имеющими бесконечно большую прочность, жесткость и длину, достаточную для того, чтобы обеспечить свободный прогиб балки и при этом смещение балки в точке В из-за изменения линейных размеров при прогибе будет происходить только по оси х. Сила трения в шарнирах равна 0, опорные стержни также шарнирно соединены с землей. При этом вертикальные стержни, обозначенные на рисунке 2 фиолетовым цветом, параллельны оси у, а горизонтальный стержень, обозначенный на рисунке 2 синим цветом, расположен на оси х, как и основная балка. Данное положение опорных стержней обеспечивает геометрически неизменяемую конструкцию. Это позволяет заменить опорные стержни тремя опорными реакциями и при расчетах обойтись тремя основными уравнениями равновесия, здесь мы никаких расчетов не производим, а потому и уравнения равновесия не приводятся (значения моментов, определенных, исходя из уравнений равновесия, даны на рисунке 219.1.а). В принципе при такой расчетной схеме расчет перемычки занимает не более получаса, причем больше всего времени уходит на сбор нагрузок. Изображаться шарнирные опоры могут по-другому, особенно для консольных балок, например так, как показано на рисунке 219.1.а), одна из опор при этом может обозначаться условно скользящей, но как бы шарнирные опоры не изображались физический смысл расчетной схемы для шарнирного закрепления на двух опорах остается неизменным.
Данную расчетную схему можно принимать для большинства строительных конструкций, имеющих две опоры и при этом относительно небольшую площадь опирания, например, при расчете деревянных, металлических и железобетонных балок перекрытия (если железобетонные балки будут изготавливаться отдельно от плиты перекрытия), для половых досок и железобетонных плит перекрытия, опирающихся на две стены, для перемычек. При этом влияние гвоздей, шурупов или раствора на работу конструкции можно не учитывать. Но
если длина опорных частей больше 1/3 длины пролета для перемычек или больше 1/8 части длины пролета для плит перекрытия в зданиях со стенами из тяжелых материалов, то имеет смысл проверить, нельзя ли рассматривать данную конструкцию, как защемленную на опорах.
С точки зрения строительной механики жесткое защемление на опорах, показанное на рисунке 219.1.б), можно заменить опорными стержнями следующим образом:
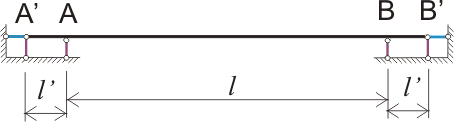
Рисунок 219.3. Замена защемления на опорах шарнирными опорами
Для того, чтобы защемление считалось жестким, значение l' должно быть значительно меньше l или стержень на участках АА' и ВВ' должен быть абсолютно жестким, при соблюдении одного из этих условий угол поворота поперечного сечения балки в точках А и В будет равен 0 или стремиться к 0. В реальности первое условие выполнимо, только если наша балка будет на опоре приварена (для металлических каркасов) или приварена и забетонирована (для железобетонных каркасов), причем не на глаз, а согласно расчету. Или нагрузка сверху и снизу на опорные участки балки l' будет значительно больше, чем нагрузка на балку, например при достаточном защемлении железобетонной плиты перекрытия между кирпичами стены. Но и этого мало. Такая балка, защемленная на двух опорах (рисунок 1.б) или имеющая 6 опорных стержней (рисунок 3), является трижды статически неопределимой балкой, со всеми вытекающими отсюда последствиями. В данном случае, как уже говорилось, расчетами мы не занимаемся, да и нет в этом необходимости, основные расчетные формулы приведены на рисунке 1.б, но использовать полученные знания уже можем.
Ну и главное отличие жестко защемленной опоры от шарнирной: угол поворота поперечного сечения балки (стержня) на жестко защемленной опоре всегда равен 0 вне зависимости от того, где и как приложена нагрузка, а на шарнирных опорах угол наклона поперечного сечения как правило максимальный. Это и дает в итоге столь ощутимую в конечном счете разницу значений прогибов.
Примеры влияния длины опорных участков
1. А теперь рассмотрим наиболее приближенный к реальности случай
Перемычка над проемом в кирпичной стене имеет опорные участки некоторой длины, к перемычке приложена равномерно распределенная нагрузка, проще говоря, на перемычку опирается кирпич. Такую перемычку можно условно рассматривать как двухконсольную балку на двух шарнирных опорах с равномерно распределенной нагрузкой. Требуется подобрать длину консолей так, чтобы изгибающий момент на опорах был равен максимальному моменту в пролете. Задача, не смотря на всю сложность формулировки, очень проста. Так как для безконсольной балки на двух шарнирных опорах максимальный изгибающий момент будет равен ql2/8, то для консольной балки с таким же пролетом l нам необходимо подобрать такую длину l', чтобы соблюдалось условие Мmax для пролета = Мна опорах = ql2/16. Почему так, здесь объяснять не буду, поверьте на слово (впрочем, по просьбам учащихся я написал отдельную статью об особенностях расчета косольных балок с симметрично загруженными консолями). Таким образом момент на опоре от распределенной нагрузки будет ql2/16 = ql'2/2. Следовательно длина опорных участков перемычки должна составлять
l' = l /(√8) ≈ 0.3535l
Например для перемычки, укладываемой над пролетом длиной 2 метра, длина одного опорного участка должна составлять не менее 0.7 м, а суммарная длина опорных участков должна составлять не менее 1.4 м, чтобы перемычку можно было рассчитывать как двухконсольную балку на двух шарнирных опорах. И если для перемычки над двухметровым пролетом такая длина опорного участка - это много, то для перемычки над проемом в 1 метр длина опорных участков в 36 см уже не кажется такой большой по сравнению с минимально требуемой в 25 см и таким образом иногда можно подобрать такие размеры перемычки, которые позволят чуть ли не в 2 раза сэкономить на материалах. Тут есть свои особенности, которые при расчетах необходимо учитывать:
- Увеличение длины опорных участков будет приводить к увеличению момента на опорах и балка будет приближаться с жестко защемленной на опорах;
- Уменьшение длины опорных участков будет приводить к увеличению момента в пролете и балка будет приближаться к бесконсольной шарнирно опертой;
- Нагрузка, принимаемая нами, как равномерно распределенная, на самом деле таковой не является, кроме того при сведении объемной нагрузки к плоской плоскость приложения такой нагрузки далеко не всегда будет совпадать с плоскостью, проходящей через центры тяжести сечений.
Учесть эти особенности можно поправочным коэффициентом, например, 1.2 или 1.3. Если мы умножим значение момента на поправочный коэффициент 1.5, то это уже получится жестко защемленная балка.
2. Еще один пример
Плита перекрытия опирается на кирпичную стену шириной 77 см (именно такая толщина стен часто требуется для обеспечения необходимой теплоизоляции современными строительными нормами, если стена дополнительно не будет утепляться), пролет плиты l = 4 метра, длина опорных участков на плиту перекрытия l' = 0.6 м. Распределенная нагрузка на плиту перекрытия q1 = 500 кг/м, распределенная нагрузка от веса кирпичной стены (в зависимости от марки и состава кирпича, высоты кладки и других причин) q2 = 4000 кг/м.
Требуется проверить, можно ли рассматривать такую плиту как балку, жестко защемленную на опорах, или как консольную балку на шарнирных опорах.
Примечание: если длина опорного участка балки меньше высоты поперечного сечения балки, то нагрузка от веса стены из-за перераспределения напряжений не учитывается и балка рассматривается, как безконсольная на шарнирных опорах. В данном случае, если высота балки h находится в пределах 10-20 см, то длина опорного участка балки значительно больше высоты сечения и потому нагрузку от веса стены нужно учитывать, при этом нужно учитывать нагрузку от всей ширины стены, так как длина опорных участков сопоставима с толщиной стены. Момент на опорах будет равен
Мопор = 4000·0.62/2 = 720 кг·м,
момент в пролете для безконсольной балки на шарнирных опорах
Mпролета = 500·42/8 = 1000 кг·м,
таким образом максимальный момент в пролете плиты перекрытия составит 280 кг·м, это меньше чем 1000/3 = 333 кг·м и потому такую плиту перекрытия следует рассматривать как жестко защемленную на опорах.
Примечание: Даже в этом случае угол поворота поперечных сечений в начале опорных участков не будет равен нулю, так как и балка и материал стены имеют не бесконечно большую жесткость. Это означает, что для более точного расчета значение пролета жестко защемленной балки следует принимать больше фактического расстояния между стенами, на которые опирается балка. Более того, расчетное значение пролета может быть даже больше длины самой балки, особенно если модуль упругости балки значительно больше модуля упругости стенового материала.
3. Еще один пример
Плита перекрытия опирается на кирпичную стену шириной 51 см (именно такая толщина стен до сих пор часто делается), пролет плиты такой же l = 4 метра, длина опорных участков на плиту перекрытия l' = 0.38 м. Распределенная нагрузка на плиту перекрытия q1 = 500 кг/м, распределенная нагрузка от веса кирпичной стены (в зависимости от марки и состава кирпича, высоты кладки и других причин) q2 = 4000 кг/м. Требуется проверить, можно ли рассматривать такую плиту как балку, жестко защемленную на опорах, или как консольную балку на шарнирных опорах. Момент на опорах будет равен
Mопор = 4000·0.382/2 = 288.8 кг·м,
момент в пролете для безконсольной балки на шарнирных опорах
Mпролета = 500·42/8 = 1000 кг·м,
Таким образом максимальный момент в пролете плиты перекрытия составит 711.2 кг·м, это больше чем 333 кг·м и потому такую плиту перекрытия следует рассматривать как консольную балку с шарнирными опорами.
Примечание: если рассматривать такую плиту перекрытия как безконсольную балку на шарнирных опорах, то максимальный изгибающий момент, на который нужно рассчитывать поперечное сечение, будет на 40% больше. Однако как и в первом примере, все не так просто и для учета неучтенных обстоятельств желательно использовать поправочный коэффициент.
Конечно же опорные площадки, на которые будет опираться балка, нужно отдельно просчитать на прочность. |
19-03-2013: Евгений
Здравствуйте!
Подскажите, пожалуйста, при расчете стены на прочность куда прикладывается сосредоточенная сила(равная опорной реакции)от плиты перекрытия с временными нагрузками? по середине площадки опирания плиты или как? я так понимаю, что с эксцентриситетом от оси стены, только с каким? И если на среднюю несущую стену опираются 2 плиты, то как в этом случае прикладывать сосредоточенные силы, чтоб рассчитать стену на прочность?
Заранее благодарю за ответ
19-03-2013: Доктор Лом
Подробный ответ на ваш вопрос в статьях "Расчет стены на прочность" (https://doctorlom.com/item237.html) и "Расчет опорной площадки стены на смятие"
(https://doctorlom.com/item246.html). Эти статьи вышли позже, но теперь поставил ссылку в самой статье.
27-07-2013: Влад
Спасибо большое за вашу работу. Давно искал, чтобы кто-нибудь мне это доступно объяснил. Из ваших объяснений почти всё понял. (перечитаю ещё раз, пойму больше)
Но не понятно откуда берётся вот это:
1000/3 = 333 кг·м
Почему делите на 3? Откуда взялась 3? Где я это упустил?
И ещё консольно-шарнирная, бесконсольно шарнирная, защемленная - это три типа балок, или разные названия.
27-07-2013: Доктор Лом
Дело в том, что для жестко защемленных балок максимальный момент в пролете в три раза меньше, чем для шарнирно опертых бесконсольных, но еще меньше быть уже не может, поэтому значение для шарнирно опертой балки было разделено на 3. После чего сравнивались значения для принятия решения по расчетной схеме.
Любая балка может быть жестко защемленной или иметь шарнирные опоры. При этом если длина шарнирно опертой балки больше чем расстояние между опорами, то значит у балки есть консоли. Жестко защемленная балка может иметь всего одну опору и тогда она может так и называться - консольная балка, пример - балконная плита
25-06-2014: Валерий Мальцев
плиты пустотные 220мм безопалубочного формования без верхней арматуры как глубоко можно заводить в стены 16-этажного здания? какой здесь нужен расчёт? в альбомах не даны чёткие критерии. Вопрос к Вам, доктор Лом. В КН 2014 06 25, Ср.
01-07-2014: Доктор Лом
Это будет зависеть от конструктивной схемы здания и параметров плиты. В любом случае отсутствие верхней арматуры значительно ограничивает длину опорной площадки.
18-11-2014: ученик
Док, дачный вопрос. Бочка с водой стоит на эдаком "столе". Диаметр бочки 0,5 м, емкость 200 л. Стол 1 х 2 м, "ножки" по габаритам крышки стола. Бочка по короткой стороне - по оси симметрии стола, по длинной - край бочки по краю "стола". Как примерно распределяется нагрузка на "ножках" по короткой и длинной сторонам и какие расчетные схемы для крышки стола: по короткой - балка с распределенной нагрузкой на среднем участке 0,5 м и по длинной - с распределенной на участке 0,5 м от начала, плюс собственные веса? Да еще же и опорный участок бочки в форме круга, по ребру бочки?
19-11-2014: Доктор Лом
Задача в сформулированном вами виде достаточно сложна (думаю, вы даже не подозреваете насколько) и просто ответить на ваш вопрос не получится.
Для начала, если ножки будут приварены к крышке, а кроме того врыты в землю или забетонированы, то у вас будет не балка на шарнирных опорах (крышка стола), а рама (с соответствующим креплением на опорах), причем чем больше длина ножек и чем меньше их жесткость, тем сильнее будет влияние ножек на общую прочность рамы. Кроме того, прочность рамы должна быть обеспечена сварными швами согласно расчету. При очень коротких или очень жестких ножках крышку стола можно рассматривать как жестко защемленную балку. При очень длинных ножках крышка стола может рассматриваться как шарнирно опертая балка
Далее, крышка стола представляет собой пластину, опертую по углам. При этом нагрузка на нее передается по контуру бочки (по окружности) только при условии бесконечно большой жесткости пластины или при нагрузке, влияние которой на прогиб пластины при имеющейся прочности можно не учитывать. Кроме того, прогиб пластины будет приводить к смещению центра тяжести бочки, а значит и к перераспределению нагрузки, что при расчетах также необходимо учитывать. К слову сказать, даже расчет пластины, опертой по контуру, на действие равномерно распределенной нагрузки - достаточно сложная задача.
Потому мой вам совет: рассчитывайте крышку как балку, на которой стоят 2 бочки с водой, при этом нагрузка является равномерно распределенной, а ножки, как стойки (колонны) с шарнирным закреплением сверху и снизу. А для пущей надежности можете умножить значение нагрузки на коэффициент надежности по нагрузке 1.5.
20-11-2014: ученик
Док, спасибо большое. Я примерно так и планирую, это для варианта, если одна бочка пустая. Раскосы от средин сторон стола к "ножкам" помогут перенести нагрузку на опорные ножки? высота ножек 2 м. Я так понимаю, нагрузка на ножках = опорным реакциям + е?
21-11-2014: Доктор Лом
При раскосах у вас точно будет рама. Раскосы не только будут дополнительно передавать нагрузку от крышки ножкам, но и обеспечивать геометрическую неизменяемость системы в соответствующих плоскостях. Для упрощения расчетов вы можете рассматривать ножки как стойки длиной от крепления раскоса до низа с жестким защемлением в месте крепления раскоса в соответствующей плоскости. А нагрузка на все ножки при упрощенном расчете будет одинаковой, приблизительно 100 кг (если расчет на 2 бочки по 200 л).
06-02-2015: Алексей
Здравствуйте. Никак не пойму один момент: почему при определении "Максимального момента в пролете плиты" (таким образом максимальный момент в пролете плиты перекрытия составит 711.2 кг·м), Вы вычетаете из Mпролета Mопор (1000-288,8= 711,2)
06-02-2015: Доктор Лом
Просто ответить на ваш вопрос не получится, посмотрите статью "Консольная балка с загруженными консолями", ссылка на статью в первом примере.
13-08-2015: Юрий
Обоснуйте пожалуйста применение равенства Мmax для пролета = Мна опорах. Я вот не вижу логики в нём.
Я считаю, если мы хотим получить схему, эквивалентную жёсткой заделке, то мы должны стремиться получить в ней тот же характер распределения усилий. Другими словами (ql^2)/12=(ql'^2)/2, Откуда l’=l/?6?0.41l. Подставим это выражение в формулу момента в пролёте для схемы с консолями
q(l^2-4l’^2)/8=q(l^2-4l^2/6)/8=[ql^2-2al^2/3]/8=[ql^2/3]/8=ql^2/24,
получился момент в пролёте для схемы с жёсткой заделкой.
Всё логично.
13-08-2015: Доктор Лом
Для начала я ни на чем не настаиваю, а лишь привел пример применения приведенных выше теоретических выкладок. Стремления к схеме, эквивалентной жесткой заделке, у меня не было изначально, потому что:
Во-вторых, равенство моментов в пролете и на опорах позволяет максимально эффективно использовать материал балки, например металлической или деревянной. Соответственно сечение такой балки при максимальном моменте М =(ql^2)/16 может быть меньше, чем при М =(ql^2)/12. А в-третьих, общая длина балки (с учетом опорных участков) при этом будет меньше, чем при условии жесткой заделки, а потому с учетом предыдущего пункта стоимость такой балки может быть ощутимо меньше.
17-08-2015: waxgem
ОК) Полностью согласен с максимальной экономичностью решения. Единственное "но"- годится для небольших пролётов, и нужно смотреть по ситуации рациональность применения (для малых нагрузок перемычка конструктивная с минимальным опиранием)
26-10-2016: polivalkin
Здравствуйте, подскажите значение постоянной EI или где его взять?
26-10-2016: Доктор Лом
EI - это не постоянная, а произведение модуля упругости Е на момент инерции I. Значение модуля упругости зависит от материала балки (больше подробностей смотрите в статье "Расчетные сопротивления и модули упругости для различных строительных материалов"), а значение момента инерции от геометрической формы поперечного сечения балки (больше подробностей смотрите в статье "Момент инерции и момент сопротивления").
|

