Расстояние в свету между стенами - пролет фермы - l = 6 м, кровля - волнистые асбестоцементные листы, уклон кровли α = 30о, при таком уклоне длина стропильных ног будет составлять lст = 3.464 м (возможное наличие кобылок для упрощения расчетов не учитывается, высота фермы f = 1.732 м (проблемы определения сторон треугольника - длины стропильной ноги и высоты фермы, относятся больше к геометрии, чем к строительной механике, а потому здесь и далее не рассматриваются).
Основные принципы расчета ферм изложены отдельно, здесь мы на этом останавливаться не будем. Здесь же отметим, что расчет и простейших трехстержневых ферм и трехшарнирных арок на действие равномерно распределенной нагрузки по общепринятой упрощенной методике приводит к тому, что:
1. Значение опорных реакций может оказаться заниженным.
2. Не учитывается наличие дополнительных нормальных напряжений в наклонных стержнях фермы или арки, а также возможное появление дополнительных нормальных напряжений в горизонтальном стержне фермы
Ну а теперь начнем расчет. При общепринятой методике расчетная схема фермы будет выглядеть так:
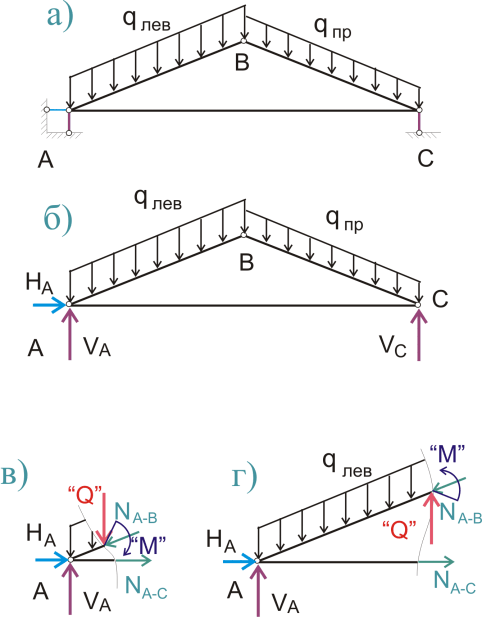
Рисунок 446.1. Расчетная схема трехстержневой треугольной симметричной фермы.
Как определить нагрузки на стропила, изложено отдельно, здесь же мы просто отметим, что снег - материя очень не постоянная, он может лежать равномерно на крыше, а может переноситься ветром с одного ската на другой. Потому для дальнейших расчетов более правильно будет принять наиболее неблагоприятное сочетание нагрузок, когда на одном скате снега больше и тогда расчетная распределенная нагрузка будет составлять qлев = 326.1 кг/м, а на втором скате снега меньше и расчетная нагрузка на вторую часть фермы будет составлять:
qпр = qcт + qo + qш +qs = 3.75 + (6.25 + 16.77 + 180х0.75х1.2)1.1 = 207.3 кг/м
Так как при уклоне кровли 30о над кровлей при воздействии ветровых нагрузок будет создаваться разрежение (при h/l ≤ 1), то влияние горизонтальной и вертикальной составляющей ветровой нагрузки для упрощения расчетов учитывать не будем, небольшой запас по прочности не помешает, а расчеты при этом упростятся.
Упрощенный расчет
Чтобы еще более упростить расчеты, то можно допустить, что нагрузка на оба ската кровли будет одинаковой, т.е. и нагрузка и ферма - симметричные. Это даст дополнительный (и опять не очень большой) запас прочности, но зато позволит достаточно просто и легко определить опорные реакции, продольные и поперечные силы, а также моменты, действующие на стержни фермы.
Таким образом, принимая максимальную нагрузку q = 326.1 кг/м действующей на оба наклонных стержня фермы получим следующие результаты:
Вертикальные опорные реакции
VА = VС = ql/2 = 326.1·6/2 = 978.3 кг (446.1.1)
Для определения значения горизонтальной составляющей НА мы можем составить дополнительное уравнение моментов относительно точки В:
∑МВ = VАl/2 - VCl/2 + ql2/8 - ql2/8 - HAf = 0 (466.1.2)
HA = (ql2/4 - ql2/4 + ql2/8 - ql2/8)/f = 0/1.732 = 0 (466.3.1)
Определим значения поперечных сил "Q", которые возникают в поперечных сечениях наклонных стержней фермы при действии равномерно распределенной нагрузки. В данном случае наклонные стержни рассматриваются как наклонные балки. А чтобы еще более упростить расчет, исключив из него изгибающие моменты, мы будем рассматривать сечения, максимально близкие к узлам фермы, тогда при симметричной нагрузке "Q" = ql/4.
Теперь, воспользовавшись методом сечений (который в данном случае тождественен методу вырезания узлов, так как ферма - простейшая), определим продольные силы в стержнях фермы.
Сначала рассмотрим расчетную схему 466.1.в). Предположим, что распределенная нагрузка вообще не передается на стержень А-В, т.е. сечение проходит практически по узлу А. Составим уравнение изгибающих моментов относительно точки В:
∑МВ = VАl/2 - "Q"l/2 - NA-Cf = 0 (466.2.1)
NA-C = (VАl/2 - "Q"l/2)/f = (ql2/4 - ql2/8)/f =(326.1·62/8)/1.732 = 847.258 кг (466.3.1)
Тогда согласно уравнению моментов относительно точки С:
∑МС = VАl - "Q"l - NA-Blsin30° = 0 (466.2.2)
NA-B = (VАl - "Q"l)/lsin30° = (ql/2 -ql/4)/0.5 = ql/2 = 978.3 кг (466.3.2)
Так как и ферма и нагрузки - симметричные, то и усилие в стержне В-С будет равно усилию в стержне А-В.
Вроде бы все нормально, но если мы рассмотрим те же стержни, но на этот раз используя расчетную схему 466.1.г), предполагая, что на этот раз сечение проходит практически по узлу В, т.е. распределенная нагрузка на стержень А-В передается полностью, то уравнения моментов будут иметь уже другой вид
∑МВ = VАl/2 - ql2/8 - NA-Cf = 0 (466.4.1)
NA-C = (VАl/2 - ql2/8)/f = (978.3·6/2 - 326.1·62/8)/1.732 = 847.258 кг (466.5.1)
Согласно расчетной схеме 466.1.г).
∑МС = VАl + "Q"l/2 - 3ql2/8 - NA-Blsin30° = 0 (466.4.2)
NA-B = (ql/2 + ql/8 - 3ql/8)/0.5 = ql/2 = 978.3 кг (466.5.2)
Пока все сходится, для большей уверенности в точности расчетов проверим соблюдение уравнений статического равновесия, в частности уравнения проекций сил на основные оси. При проверке по первой расчетной схеме:
∑Qу = VA - "Q" - NA-Bsin30° = ql/2 -ql/4 -ql/4 = 0 (466.6.1)
∑Qх = NА-C + HA - NA-Bcos30° = 847.26 - 978.3·0.866 = 0.05 кг ≈ 0 (466.7.1)
при проверке по второй расчетной схеме
∑Qу = VA + "Q" - ql/2 - NA-Bsin30° = ql/2 + ql/4 - ql/2 - ql/4 = 0 (466.6.2)
∑Qх = NА-C + HA - NA-B/cos30° = 847.258 - 978.3·0.866 = 0.05 кг ≈ 0 (466.7.2)
Все сходится. Посмотрим, что получается при действии несимметричной распределенной нагрузки на нашу ферму.
Более точный расчет
Так как нагрузка действующая на ферму - не симметричная, то и опорные реакции будут разными. Для определения опорных реакций составим уравнение моментов относительно точки, расположенной на опоре А:
∑МА = qлевl2/8 + qпр(l/2 + l/4)l/2 - VСl = 0 (446.8)
VС = qлевl/8 + 3qпрl/8 = (326.1 + 3·207.3)6/8 = 711 кг (446.9.1)
тогда значение вертикальной реакции на левой опоре, на основании одного из уравнений статического равновесия составит:
VА = (qлев + qпр)b/2 - VС = (326.1 + 207.3)3 - 711 = 889.2 кг (446.9.2)
Для определения НА опять составим уравнения моментов относительно точки В:
∑МВ = VАl/2 - VCl/2 + qпрl2/8 - qлевl2/8 - HAf = 0 (466.10.1)
HA = (889.2·3 - 711·3 + 207.3·36/8 - 326.1·36/8)/f = (534.6 - 534.6)/1.732 = 0 (466.10.2)
Как видим, даже при несимметричной нагрузке горизонтальная составляющая опорной реакции также равно нулю. Проверим значение продольной силы, действующей на горизонтальный стержень. При первой основной расчетной схеме:
∑МВ = VАl/2 - "Q"l/2 - NA-Cf = 0 (466.2.1)
NA-C = (VАl/2)/f = (889.2·6/2 - 326.1·36/8)/1.732 = 692.93 (466.11.1)
При первой зеркальной расчетной схеме:
∑МВ = VСl/2 - "Q"l/2 - NA-Cf = 0 (466.2.2)
NA-C = (711·6/2 - 207.3·36/8)/1.732 = 692.93 кг (466.11.2)
Напомню, именно такой результат мы получили при расчете трехшарнирной арки с затяжкой. Подобным образом можно определить напряжения и в остальных стержнях фермы, но в данном случае такой необходимости нет.
И тут хотелось бы обратить внимание на одну маленькую, но очень важную с моей точки зрения деталь.
Дело в том что у трехшарнирной арки два стержня - горизонтальные связи, соответственно в одном горизонтальном стержне - затяжке арки или горизонтальном стержне фермы значение продольной силы вроде бы должно увеличиться в 2 раза и составлять:
NA-C = 692.93 + 692.93 = 1385.85 кг
Такой же вывод можно сделать, исходя из того, что продольные силы в стержне NA-C при рассмотрении по основной и зеркальной расчетной схемам направлены в разные стороны, т.е. горизонтальный стержень растягивается как при воздействии нагрузок с левой стороны фермы, так и с правой стороны.
Тем не менее, исходя из условий статического равновесия продольная сила, действующая на горизонтальный стержень, все-таки составляет 692.93 кг.
Попробуем проверить, так ли это, еще одним способом.
Например, если мы будем условно рассматривать нашу ферму как некую балку переменного сечения, то момент, возникающий посредине такой балки составит:
М = VAl/2 - qлевl2/8 = 889.2·3 - 326.1·36/8 = 2667.6 - 1467.45 = 1200.15 кгм (466.12.1)
А так как балка у нас достаточно условная, т.е. есть как бы только верхняя часть сечения - наклонный стержень и нижняя часть сечения - горизонтальный стержень, этот момент мы можем разложить на пару сил, возникающих в стержнях. Соответственно при высоте сечения балки f = 1.732 м продольная сила действующая на горизонтальный стержень, составит:
NA-C = M/f = 1200.15/1.732 = 692.93 кг (466.13.1)
Эта сила будет вызывать растяжение в горизонтальном стержне. Кроме того, мы можем также определить и сжимающее усилие в наклонных стержнях в рассматриваемом сечении:
NA-B = NB-C = M/fcosa = 692.93/0.866 = 800.14 кг (466.13.2)
Как видим, вне зависимости от принимаемой расчетной схемы результат у нас одинаковый. | 
