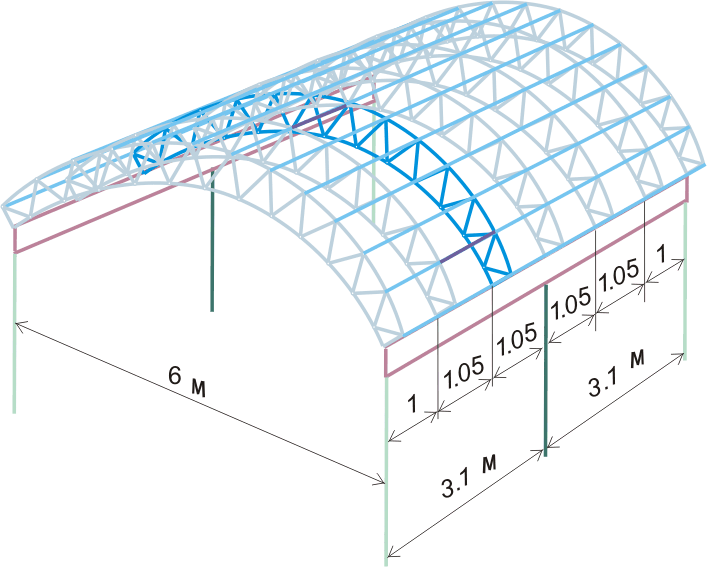
Рисунок 293.1. Общая предварительная схема арочной галереи.
Расчетной нагрузкой для ферм будет снеговая нагрузка, нагрузка от веса поликарбоната, балок обрешетки и собственного веса ферм. Для упрощения расчетов можно рассматривать все эти нагрузки как сосредоточенные в узлах фермы.
В действительности, при использовании сотовых поликарбонатных листов и при расположении балок обрешетки вровень с верхним поясом фермы часть нагрузки будет передаваться не в виде сосредоточенной нагрузки в узлах фермы, а в виде равномерно распределенной нагрузки на стержни верхнего пояса. Однако даже при пролете между фермами, равном пролету между балками обрешетки, нагрузка, передаваемая листами поликарбоната непосредственно на стержни верхнего пояса фермы, будет в 8-10 раз меньше, чем нагрузка, приходящаяся на балки обрешетки, а значит, на узлы фермы. Если пролет между балками обрешетки будет в два раза меньше пролета между фермами, то значение распределенной нагрузки, передаваемой непосредственно на стержни верхнего пояса фермы, уменьшится еще в несколько раз. Таким образом для упрощения расчетов фермы нагрузку на ферму можно рассматривать как несколько сосредоточенных нагрузок, приложенных в узлах фермы. Более того, распределенная нагрузка будет уменьшать значение момента, возникающего в верхних стержнях из-за их непрямолинейности и потому расчет без учета того, что часть нагрузки передается в виде распределенной, будет не только более простым, но и более надежным, так как обеспечит дополнительный запас по прочности. А чтобы сомнений в правильности выбранного пути не оставалось, можно увеличить сечение стержней верхнего пояса на 3-5% в зависимости от соотношения пролетов. И только если настил будет из монолитного поликарбоната, то соотношение нагрузок, передаваемых в узлах фермы и равномерно распределенных по стержням верхнего пояса фермы, следует учитывать при расчете. Однако мы такую ситуацию пока не рассматриваем.
При расстоянии между верхними узлами фермы около 63 см и пролете между фермами 105 см соотношение пролетов составляет 105/63 = 1.67 раза, поэтому наше допущение о передаче нагрузок только в узлах фермы вполне приемлемо. Вот только определить эти самые сосредоточенные нагрузки в узлах фермы будет не так уж и просто. Когда мы рассчитывали сотовый поликарбонат и балки обрешетки, то выяснили, что снеговая нагрузка - одна из главных расчетных нагрузок - является не постоянной и неравномерно распределенной. Это означает, что во-первых ферму необходимо рассчитывать на 2 варианта загружения, а во-вторых, при первом варианте загружения, когда изменение снеговой нагрузки по длине пролета фермы описывается уравнением косинуса, для определения суммирующей сосредоточенной нагрузки потребуется множество вычислительных операций. Точнее все эти вычислительные операции мы должны были сделать раньше, когда рассчитывали сотовый поликарбонат и балки обрешетки, так как опорные реакции для многопролетной балки - листа сотового поликарбоната - это и есть сосредоточенные нагрузки для фермы, передаваемые балками обрешетки в узлы. Тем не менее при расчетах и сотового поликарбоната и балок обрешетки большой необходимости в точных расчетах не было, так как возможное уменьшение расчетных величин, таких как момент сопротивления или деформация прогиба на 2-10% - это конечно хорошо, но все это с лихвой можно перекрыть соответствующим коэффициентом надежности конструкции.
При расчете арочной фермы также можно упростить вычисления, приняв нагрузку равномерно распределенной, однако ферма - это единая конструкция и такой запас может оказаться чрезмерным, поэтому имеет смысл повозиться с расчетом фермы немного больше. Впрочем, значения сосредоточенных нагрузок все равно будут приблизительными.
Расчет арочной фермы на 1 вариант снеговой нагрузки
Для начала определим средние значения коэффициентов μ для каждого пролета верхнего пояса балки (так как ферма симметричная, то достаточно это сделать только для одной половины фермы). Для этого нужно знать значения углов наклона касательных в этих точках. Если верить науке геометрии, то получается, что в середине первого (крайнего) пролета угол наклона будет 47.823о, во втором - 39.128о, в третьем - 30.433о, в четвертом - 21.737о, в пятом - 13.043о, в шестом - 4.348о (угол между узлами верхнего пояса фермы составляет 104.34/12 = 8.695о). Тогда
для 1 пролета среднее значение μ = cos1.8·47.823 = 0.068, l1 = 0.6239·cos47.823 = 0.4189 м, Q1ср = 180·0.068·0.4194 = 5.13 кг
для 2 пролета μ = 0.335, l2 = 0.484 м, Q2ср = 29.21 кг
для 3 пролета μ = 0.5767, l3 = 0.5379 м, Q3ср = 55.91 кг
для 4 пролета μ = 0.7757, l4 = 0.5795 м, Q4ср = 81.03 кг
для 5 пролета μ = 0.9172, l5 = 0.6078 м, Q5ср = 100.47 кг
для 6 пролета μ = 0.9906, l6 = 0.6221 м, Q6ср = 111.08 кг
При этом, как мы уже говорили, опорные реакции в узлах не будут равны половине сосредоточенной нагрузки, условно приложенной в середине пролета, тем не менее для упрощения решения задачи такое допущение вполне приемлемо. Тогда сосредоточенные нагрузки от снега в узлах фермы составят
Qs1 = 5.13/2 = 2.565 кг
Qs2 = 2.565 + 29.21/2 = 17.17 кг
Qs3 = 14.605 + 55.91/2 = 42.56 кг
Qs4 = 27.955 + 81.03/2 = 68.47 кг
Qs5 = 40.515 + 101.47/2 = 91.49 кг
Qs6 = 50.735 + 111.08/2 = 106.275 кг
Qs7 = 111.08 кг
Значения распределенных нагрузок от веса сотового поликарбоната и балок обрешетки мы определили ранее, воспользуемся этими значениями. Тогда
Qп1 = 1.905·1.05/2 = 1 кг
Qп2 = 1.905·1.05 = 2 кг
Значения сосредоточенной нагрузки от веса поликарбоната в остальных узлах фермы (кроме последнего) будут такими же, как во втором узле.
Qб1 = 4.22·1.05/2 = 2.22 кг
Qб2 = 4.22·1.05 = 4.43 кг
Нагрузка от собственного веса фермы нам по умолчанию не известна, но предположим, что ферма будет изготавливаться из квадратной профильной трубы сечением 50х3 мм, тогда с учетом геометрии фермы и особенностей изготовления сосредоточенная нагрузка от собственного веса будет в 2.5-3 раза больше, чем нагрузка от балок обрешетки и составит
Qф1 = 2.22·3 = 6.66 кг
Qф2 = 4.43·3 = 13.29 кг
Теперь мы можем собрать сосредоточенные нагрузки для всех узлов фермы
Q1 = 2.57 + 1 + 2.22 + 6.66 = 12.45 кг
Q2 = 17.17 + 2 + 4.43 + 13.29 = 36.89 кг
Q3 = 62.28 кг
Q4 = 88.19 кг
Q5 = 111.21 кг
Q6 = 126 кг
Q7 = 130.8 кг, Q7/2 = 65.4 кг
А теперь можно уже определить значение опорных реакций для фермы. Так как ферма у нас симметричная и нагрузки приложены симметрично, то опорные реакции будут равны между собой и будут составлять
VA = VB = Q1 +Q2 + Q3 + Q4 + Q5 + Q6 +Q7/2 = 12.45 + 36.89 + 62.28 + 88.19 +111.21 + 126 + 65.4 = 502.42 ≈ 502.4 кгс
Значение горизонтальной составляющей опорной реакции будет равно нулю, так как горизонтальных нагрузок в нашей расчетной схеме нет.
В итоге расчетная схема для нашей фермы будет выглядеть так:

Рисунок 293.2. Расчетная схема арочной фермы.
На рисунке 293.2 б) показаны сечения, благодаря которым можно рассчитать усилия во всех стержнях фермы с учетом того, что ферма и нагрузка на ферму является симметричной и значит достаточно рассчитывать не все стержни фермы, а чуть больше половины. А чтобы не заблудиться в густом лесу стержней, стержни и узлы ферм принято маркировать. Маркировка, показанная на рис.293.2 в) означает, что у фермы есть:
Стержни нижнего пояса: 1-а, 1-в, 1-д, 1-ж, 1-и, 1-л, 1-н;
Стержни верхнего пояса: 3-б, 4-г, 5-е, 6-з, 7-к, 8-м;
Стойка: 2-а;
Раскосы: а-б, б-в, в-г, г-д, д-е, е-ж, ж-з, з-и, и-к, к-л, л-м, м-н.
Если нужно рассчитать все стержни фермы, то лучше составить таблицу, в которую нужно внести все стержни фермы. Затем в эту таблицу будет удобно вносить полученные значения максимальных изгибающих моментов, а также растягивающих или сжимающих напряжений.
Если фермы будут изготавливаться из 1-2 видов профилей металлопроката, то достаточно рассчитать сечения стержней в наиболее нагруженных сечениях фермы. А так как на глаз определить такие максимально загруженные сечения трудно, то произведем расчет для сечений, показанных нар рисунках 293.2 г), д), ж).
сечение II-II (рис. 293.2 ж)
Так как в узлах фермы - шарниры, то и значение изгибающих моментов в узлах фермы равно нулю, а кроме того, исходя из тех же условий статического равновесия сумма всех сил относительно оси х или оси у также равна нулю. Это позволяет составить как минимум три уравнения статического равновесия (два уравнения для сил и одно для моментов), но в принципе уравнений моментов может быть столько же сколько узлов в ферме и даже больше, если использовать точки Риттера. А это такие точки в которых пересекаются две из рассматриваемых сил и при сложной геометрии фермы точки Риттера не всегда совпадают с узлами фермы. Тем не менее в данном случае у нас геометрия не очень сложная и потому для определения усилий в стержнях попробуем обойтись имеющимися узлами фермы. Но при этом опять же из соображений простоты расчета как правило выбираются такие узловые точки, уравнение моментов относительно которых позволяет сразу определить неизвестное усилие, не доводя дело до решения системы из нескольких уравнений.
Выглядит это примерно так. Если составить уравнение моментов относительно узла 2, то в нем будут всего два члена, причем один из них уже известный:
М2 = -VAl + N1-ah = 0;
N1-ah = VAl;
где l - плечо действия силы, равное расстоянию от узла 1 до узла 2 по горизонтали, согласно принятой нами расчетной схемы l = 0.25 м; h- плечо действия силы N1-a , равное кратчайшему расстоянию до линии действия силы N1-a. Так как рассматриваемый нами стержень 1-а не является прямолинейным, то h будет зависеть от места условного рассечения. Разрешается эта ситуация следующим образом: все стержни рассматриваются как прямолинейные (на рисунке 293.3 показаны зеленым цветом), а изменение геометрии стержней учитывается эксцентриситетом приложения нагрузки (на рис. 293.3 показан красным цветом), при этом максимальный эксцентриситет будет посредине криволинейного стержня. А там, где есть эксцентриситет есть изгибающий момент и его следует учитывать при подборе сечения стержней. Так как пояса фермы описываются уравнением окружности, то определить значение эксцентриситета для всех пролетов не сложно.

Рисунок 293.3. Эксцентриситеты криволинейных стержней арочной фермы.
Так как угол между узлами верхнего пояса фермы составляет 8.695о, то согласно формулы (278.1.3) величина эксцентриситета для стержней верхнего пояса составит
е = R(1 - cos(α/2)) = 411.5(1 - 0.99712) = 1.184 см. Длина условно прямолинейных стержней верхнего пояса составит
l = 2e/tg(α/4) = 62.39 см
Угол между узлами нижнего пояса составляет 93.71/12 = 7.809о, е = 0.95512 см, для крайнего стержня 1-а е = 0.23885 см. Длина условно прямолинейных стержней нижнего пояса l = 56.041 см, длина условно прямолинейного крайнего стержня l = 28.036 см.
Далее вычисляются основные геометрические параметры стержней фермы:

Рисунок 293.4. Основные геометрические параметры для стержней арочной фермы сечения II-II.
Данные, показанные на рисунке 293.4 могут показаться слишком точными, тем более, что при изготовлении фермы точность соблюдения углов и длины стержней будет гораздо меньше. Тем не менее, изготовление фермы, это одно, а расчет фермы - совсем другое. Приведенные на рисунке 293.4 значения являются приблизительными, насколько приблизительными - покажет проверка.
Теперь мы можем определить значение силы N1-a:
N1-a = VAl/h = 502.4·0.25/0.3535 = 355.304 кг
Чтобы определить напряжения в стержне N3-б составляется уравнение моментов относительно узла 3:
М3 = VAl - Q1(0.25 + 0.1986) - N3-бh = 0;
N3-б = (502.4·0.1986 - 12.45·0.4486)/0.3675 = 256.3 кг
Усилия в стержне Nа-б можно определить, составив уравнение моментов относительно узла 1:
М1 =- Q1·0.25 - N3-б·0.353 - Nа-бh= 0;
Nа-б = - (12.45·0.25 + 256.3·0.353)/0.2196 = - 426.173 кг
Знак "-" в данном случае означает, что сила будет направлена в сторону, противоположную показанной на рисунке 293.2.ж). Т.е. в стержне будут возникать растягивающие напряжения.
Проверить правильность вычислений мы можем, составив уравнения сил:
ΣQy = - Q1 +VA - N1-asin44.9о - N3-бsin47.82о + Nа-бsin6.57о = 0; -12.45 +502.4 - 250.8 - 189.93 - 48.76 = 0.46 кг
ΣQx = - Nа-бcos6.57о - N1-aсos44.9o - N3-бcos47.82o = 0; 423.37 - 251.676 - 172.1 = - 0.397 кг
Как видим, небольшая погрешность в наших вычислениях все-таки набежала. Тем не менее эта погрешность составляет менее 0.1% (0.4·100/423.37 = 0.094%), а потому можно считать ее вполне приемлемой. К тому же это еще не самые нагруженные стержни фермы. А самые нагруженные стержни располагаются как правило ближе к середине фермы, поэтому рассмотрим далее
сечение XIII-XIII (рис. 293.2. г)
Тут без геометрии стержней тоже не обойтись, кроме того нужно знать расстояния для сосредоточенных нагрузок:

Составим уравнение моментов относительно узла 14:
М14 = -3.25Q1 - 2.8313Q2 - 2.3473Q3 - 1.8094Q4 -1.23Q5 - 0.6221Q6 + 3VA + 0.5506N1-н = 0;
N1-н = (3.25·12.45 + 2.8313·36.89 + 2.3473·62.28 +1.8094·88.19 +1.23·111.21 +0.622·126 - 3·502.4)/0.5506 = - 1528.1 кг (работает на растяжение)
Уравнение моментов относительно узла 13:
М13 = -2.97Q1 - 2.5511Q2 - 2.0671Q3 - 1.5292Q4 - 0.95Q5 - 0.3419Q6 + 2.72VA - 0.5278N8-м = 0;
N8-м = (-2.97·12.45 - 2.5511·36.89 - 2.0671·62.28 - 1.5292·88.19 - 0.95·111.21 - 0.3419·126 + 2.72·502.4)/0.5278 = 1559.51 кг (работает на сжатие)
Для определения усилий в стержне Nм-н можно составить уравнение моментов относительно узла 15, но проще составить уравнение сил относительно оси х:
ΣQx = - Nм-нcos63.03 - N8-мcos4.348 - N1-н = 0;
Nм-н =(1528.1 - 1559.51·0.9971)/0.4535 = - 59.36 кг (работает на растяжение)
В данном случае знак "-" снова показывает, что сила направлена в сторону, противоположную от той, которую мы приняли при составлении расчетной схемы. Проверим правильность расчетов
ΣQу = Q7/2 - Nм-нsin63.03 - N8-мsin4.348 = 65.4 - 1559.51·0.0758 +59.36·0.8912 = 0.09 кг
В данном случае складывать все силы, действующие в узлах, не было необходимости, так как опорная реакция больше суммы сил на Q7/2.
На этом расчет стержней по первому варианту нагружения можно закончить, но для уверенности проверим еще одно
сечение IX-IX (рис. 293.2. д)
Усилия в стержнях определяются по приведенному выше алгоритму (геометрические параметры не приводятся), значения плеч действия сил для стержней, а также угол наклона стержня Nз-и определялись графически. Сначала составим уравнение моментов относительно узла 9:
М9 = -1.8753Q1 - 1.4564Q2 - 0.9274Q3 - 0.4345Q4 + 1.6253VA - 0.4911N6-з = 0;
N6-з = - (1.8753·12.45 + 1.4564·36.89 + 0.9274·62.28 +0.4345·88.19 - 1.6253·502.4)/0.4911 = 1311.6 кг
Уравнение моментов относительно узла 10:
М10 = -2.02Q1 - 1.6014Q2 - 1.1741Q3 - 0.5795Q4 + 1.7753VA + 0.5132N1-и = 0;
N1-и = - (-2.02·12.45 - 1.6014·36.89 - 1.1741·62.28 - 0.5795·88.19 + 1.7753·502.4)/0.5132 = - 1303.68 кг (работает на растяжение)
Для определения усилий в стержне Nз-и можно составить уравнение моментов относительно узла 11, но проще составить уравнение сил относительно оси х:
ΣQx = - Nз-иcos76.95 - N6-зcos21.737 - N1-иcos15.6175 = 0;
Nз-и =(1303.68·0.9631 - 1311.6·0.93)/0.2258 = 164.8 кг
Проверим правильность расчетов
ΣQу = Q5 + Q6 + Q7/2 - Nз-иsin76.95 - N6-зsin21.737 - N1-иsin15.6175 = 65.4 + 126 + 111.21 - 1311.6·0.3703 - 164.8·0.9741 + 1303.68·0.2692 = 7.3 кг
В данном случае погрешность набежала намного больше из-за графического определения значений плеч действия сил и угла наклона одного из стержней, но все равно эта погрешность находится в пределах 1%, а потому вполне допустима, тем более, что в данном сечении усилия в стержнях не максимальные.
Расчет арочной фермы на 2 вариант снеговой нагрузки
В принципе, чтобы обеспечить достаточный запас, можно увеличить полученные максимальные усилия для стержней раза в 2 и на том расчет закончить, но раз уж мы взялись рассчитывать ферму по всем правилам, то доведем расчет до конца, тем более, что все основные геометрические параметры фермы нам уже известны. А так как бóльшие нагрузки находятся ближе к опорам, то вполне может оказаться, что нагрузка в максимально нагруженных стержнях будет меньше.
Единственное отличие от расчета по первому варианту нагрузки будет в том, что нагрузка по второму варианту будет не симметричная. Тогда
для 1 пролета среднее значение μ = 2.4sin1.4·47.823 = 2.208, l1 = 0.6239·cos47.823 = 0.4189 м, Q1ср = 180·2.208·0.4189 = 166.5 кг
для 2 пролета μ = 1.9606, l2 = 0.484 м, Q2ср = 170.81 кг
для 3 пролета μ = 1.62, l3 = 0.5379 м, Q3ср = 156.85 кг
для 4 пролета μ = 1.2156, l4 = 0.5795 м, Q4ср = 126.8 кг
для 5 пролета μ = 0.752, l5 = 0.6078 м, Q5ср = 82.27 кг
для 6 пролета μ = 0.2545, l6 = 0.6221 м, Q6ср = 28.5 кг
Для остальных - симметричных - пролетов изменится только значение коэффициента µ, а именно уменьшится в 2 раза.
для 7 пролета μ = 0.2545, l6 = 0.6221 м, Q7ср = 14.25 кг
для 8 пролета μ = 0.752, l5 = 0.6078 м, Q8ср = 41.14 кг
для 9 пролета μ = 1.2156, l4 = 0.5795 м, Q4ср = 63.4 кг
для 10 пролета μ = 1.62, l3 = 0.5379 м, Q3ср = 78.43 кг
для 11 пролета μ = 1.9606, l2 = 0.484 м, Q2ср = 85.41 кг
для 12 пролета μ = 2.208, l1 = 0.4189 м, Q2ср = 83.25 кг
При этом, как мы уже говорили, опорные реакции в узлах не будут равны половине сосредоточенной нагрузки, условно приложенной в середине пролета, тем не менее для упрощения решения задачи такое допущение вполне приемлемо. Тогда сосредоточенные нагрузки от снега в узлах фермы составят
Qs1 = 166.5/2 = 83.25 кг
Qs2 = 83.25 + 85.41 = 168.66 кг
Qs3 = 85.41 + 78.43 = 163.84 кг
Qs4 = 78.43 + 63.4 = 141.83 кг
Qs5 = 63.4 + 41.14 = 104.54 кг
Qs6 = 41.14 + 14.25 = 55.39 кг
Qs7 = 14.25 +14.25/2 = 21.38 кг
Qs8 = 7.13 + 41.14/2 = 27.7 кг
Qs9 = 20.57 + 63.4/2 = 52.27 кг
Qs10 = 31.7 + 78.43/2 = 70.92 кг
Qs11 = 39.22 + 85.41/2 = 81.93 кг
Qs12 = 42.71 + 83.25/2 = 84.34 кг
Qs13 = 41.63 кг
Тогда сосредоточенные нагрузки для всех узлов фермы
Q1 = 83.25 + 1 + 2.22 + 6.66 = 93.13 кг
Q2 = 168.66 + 2 + 4.43 + 13.29 = 188.38 кг
Q3 = 183.56 кг
Q4 = 161.55 кг
Q5 = 124.26 кг
Q6 = 75.11 кг
Q7 = 41.1 кг
Q8 = 47.42 кг
Q9 = 72 кг
Q10 = 90.64 кг
Q11 = 101.65 кг
Q12 = 104.06 кг
Q13 = 51.51 кг
Так как нагрузки приложены не симметрично, то опорные реакции следует определять по уравнению моментов. Для определения опорной реакции VA нужно составить уравнение моментов относительно точки приложения опорной реакции VB:
6VA -6.25Q1 - 5.83.13Q2 - 5.3473Q3 - 4.8094Q4 - 4.23Q5 - 3.6221Q6 - 3Q7 - 2.3779Q8 - 1.77Q9 - 1.1906Q10 - 0.6257Q11 - 0.1687Q12 + 0.25Q13
VA = (582.0625 + 1098.5 + 981.55 + 776.96 + 525.62 + 272.055 +123.3 + 112.76 + 127.44 + 107.916 + 63.6 + 17.55 - 12.8775)/6 = 796.07 кгс
Теперь можно рассчитать стержни в максимально нагруженном сечении. Расчет упрощает то, что в имеющиеся формулы достаточно подставить новые значения сосредоточенных нагрузок.
сечение XIII-XIII (рис. 293.2. г)
М14 = -3.25Q1 - 2.8313Q2 - 2.3473Q3 - 1.8094Q4 - 1.23Q5 - 0.6221Q6 + 3VA + 0.5506N1-н = 0;
N1-н = (3.25·93.13 + 2.8313·188.38 + 2.3473·183.56 +1.8094·161.55 +1.23·124.26 +0.622·75.11 - 3·796.07)/0.5506 = - 1143.17 кг (работает на растяжение)
М13 = -2.97Q1 - 2.5511Q2 - 2.0671Q3 - 1.5292Q4 - 0.95Q5 - 0.3419Q6 + 2.72VA - 0.5278N8-м = 0;
N8-м = (-2.97·93.13 - 2.5511·188.38 - 2.0671·183.56 - 1.5292·161.55 - 0.95·124.26 - 0.3419·75.11 + 2.72·796.07)/0.5278 = 1208.66 кг (работает на сжатие)
ΣQx = - Nм-нcos63.03 - N8-мcos4.348 - N1-н = 0;
Nм-н =(1143.17 - 1208.66·0.9971)/0.4535 = - 136.68 кг (работает на растяжение)
Так как максимальныеу силия в стержнях сечения XIII-XIII при 2 варианте снеговой нагрузки меньше, чем при первом варианте, то дополнительно проверять точность расчетов не будем, а лучше рассчитаем стержни верхнего и нижнего пояса для
сечения IX-IX (рис. 293.2. д)
М9 = -1.8753Q1 - 1.4564Q2 - 0.9274Q3 - 0.4345Q4 + 1.6253VA - 0.4911N6-з = 0;
N6-з = - (1.8753·93.13 + 1.4564·188.38 + 0.9274·183.56 +0.4345·161.55 - 1.6253·796.07)/0.4911 = 1230.75 кг
М10 = -2.02Q1 - 1.6014Q2 - 1.1741Q3 - 0.5795Q4 + 1.7753VA + 0.5132N1-и = 0;
N1-и = - (-2.02·93.13 - 1.6014·188.38 - 1.1741·183.56 - 0.5795·161.55 + 1.7753·796.07)/0.5132 = - 1197.06 кг (работает на растяжение)
А еще проверим усилия в стержне Nа-б, но для этого сначала нужно определить усилия в стержне N3-б:
сечение II-II (рис. 293.2 ж)
М3 = 0.1986VA - 0.4486Q1 - 0.3675N3-б = 0;
N3-б = (796.07·0.1986 - 93.13·0.4486)/0.3675 = 316.52 кг
М1 = - 0.25Q1 - 0.353N3-б - 0.2196Nа-б = 0;
Nа-б = - (93.13·0.25 + 316.52·0.353)/0.2196 = - 614.82 кг
Как видим, при 2 варианте загружения напряжения в стержнях верхнего и нижнего пояса будут меньше, а в раскосах больше. Используем эти данные для дальнейших расчетов.
Подбор сечения
Самым загруженным является стержень 8-м, на который действует продольная сжимающая сила N8-м = 1559.51 кг. Однако кроме этого следует учесть и максимальный эксцентриситет приложения этой продольной силы, который мы определили ранее. Тогда
σ = N/φF + Ne/W ≤ R
Расчет сжатых стержней ничем не отличается от расчета колонн, поэтому далее приводятся только основные этапы расчета без подробных пояснений.
по таблице 1 (см. ссылку выше) определяем значение μ = 0.5 если верхний и нижний пояс будут выгибаться из цельной трубы. Если труба будет свариваться в нескольких местах, то тогда для надежности лучше принять коэффициент μ = 0.75. Однако нормативные документы, в частности СНиП II-23-81*(1990) "Стальные конструкции", рекомендуют принимать μ = 0.8-1. Насколько справедливо такое требование в случае, если пояс фермы делается из одной трубы - решать вам.
Когда мы рассчитывали балки обрешетки для сотового поликарбоната то одним из вариантов была квадратная профильная труба 30х30х3.5 мм. По сортаменту для квадратных профильных труб площадь сечения такой трубы составит F = 3.5 см2 (радиус инерции i = √(I/F) = 1.066 см), момент сопротивления W = 2.65 см3, проверим, подходит ли эта труба для поясов фермы, так как делать пояса из трубы меньшего сечения эстетически нецелесообразно:
При радиусе инерции, равном i = 1.066 см, значение коэффициента гибкости составит
λ = μl/i = 63·0.75/1.066 = 44.32 ≈ 45
тогда по таблице 2 коэффициент изгиба φ = 0.875 (для стали С235 прочностью Ry = 2350 кгс/см2, определяется интерполяцией значений 2050 и 2450)
1559.51/(0.875·3.5) + 1559.51·1.184/2.65 = 1206 кгс/см2 < Ry = 2350 кгс/см2;
Примечание: Если расчетное сопротивление профильной трубы, которая будет использоваться для изготовления фермы, известно, то следует принимать известное значение расчетного сопротивления, если расчетное сопротивление не известно, то лучше принимать значение, минимальное из возможных, как в данном случае.
Так как раскосы фермы будут прямолинейными, т.е. эксцентриситета приложения сил не будет, да и сами напряжения, действующие в поперечных сечениях раскосов, значительно меньше, чем в стержнях верхнего и нижнего пояса, то для раскосов можно подбирать трубы, исходя из конструктивных соображений.
Например, максимальная растягивающая продольная сила будет действовать на стержень а-б Nа-б = - 614.82 кг, при заданном расчетном сопротивлении для обеспечения прочности потребуется труба сечением не менее
F = N/R = 614.82/2350 = 0.27 см2
Даже у трубы 10х10х1 мм сечение больше. Однако чем тоньше стенки трубы, тем труднее их аккуратно сварить. А так как этот и некоторые другие стержни будут работать на растяжение, то сварка это самое растяжение должна выдерживать, т.е. раскосы лучше делать минимум из 15 или 20 трубы.
Примечание: если стержни для верхнего и нижнего пояса будут выгибаться на станке, то сгибание лучше производить в точках, максимально приближенных к узлам фермы. Тогда остаточные напряжения не будут сильно влиять на несущую способность стержней и в итоге ферму действительно можно рассматривать как некую конструкцию с шарнирами в узлах. Если точки изгибания не будут приходиться на узлы фермы, то для надежности лучше принять еще большее сечение стержней (или оставить такое как есть с учетом того, что запас по прочности у нас хороший), чтобы исключить образование дополнительных пластических шарниров в стержнях фермы.
Вот в принципе и все, дальше наступает увлекательный этап поиска оптимального варианта. Например, можно увеличить шаг между фермами, чтобы в итоге пришлось делать не 7 ферм, как показано на рисунке 293.1, а 4 фермы, также можно увеличивать стрелу арки верхнего или нижнего пояса и много чего еще. Но остановимся пока на том, что есть.
Все необходимые условия по прочности и устойчивости нами соблюдены. А если учесть, что в стержнях фермы могут возникать дополнительные растягивающие или сжимающие усилия, например, при неравномерном проседании фундамента колонн, или в результате увеличения значения эксцентриситета при изготовлении фермы, то полученный запас не покажется таким уж большим. Как говорили проектировщики старого поколения: "больше профиль - меньше срок".
Как определить прогиб расчитанной фермы и почему в стержнях верхнего пояса возникает сжатие, а в стержнях нижнего - растяжение (хотя по геометрии вроде как везде сжатие должно быть), рассказывается отдельно.
Примечание: При уменьшении количества ферм пролет балок обрешетки значительно увеличивается и значит для балок обрешетки также придется использовать профильные трубы большего сечения. Но это и есть тонкости проектирования и поиска оптимального варианта.
Определить значения усилий в стержнях фермы можно и чисто графическим методом, если построить диаграмму Максвелла-Кремоны. Однако с учетом сложной геометрии нашей фермы, сделать это будет все равно не просто, в частности потребуется предварительно вычислить углы наклона к горизонтали всех стержней фермы.
И еще, по большому счету данную арочную ферму следует рассматривать скорее как арку сквозного сечения, чем простую ферму. Т.е. при расчете такой фермы более правильно будет учитывать горизонтальные опорные реакции, возникающие в процессе деформации фермы под нагрузкой, которые мы не учитывали. Тем не менее, расчет данной фермы как простой (с учетом имеющейся жесткости фермы), дает относительно небольшую погрешность, а прогиб арочной фермы из-за отсутствия затяжки следует учесть при расчете опор фермы, например, колонн.
Но как бы то ни было, изготовлять фермы - большая морока, а пролет относительно небольшой и можно сделать для такого пролета арку просто из профильной трубы. | 
