Расчет криволинейного бруса с большим радиусом кривизны почти ничем не отличается от расчета обычного прямолинейного бруса.
Так как основные геометрические параметры арки и действующие нагрузки нам уже известны
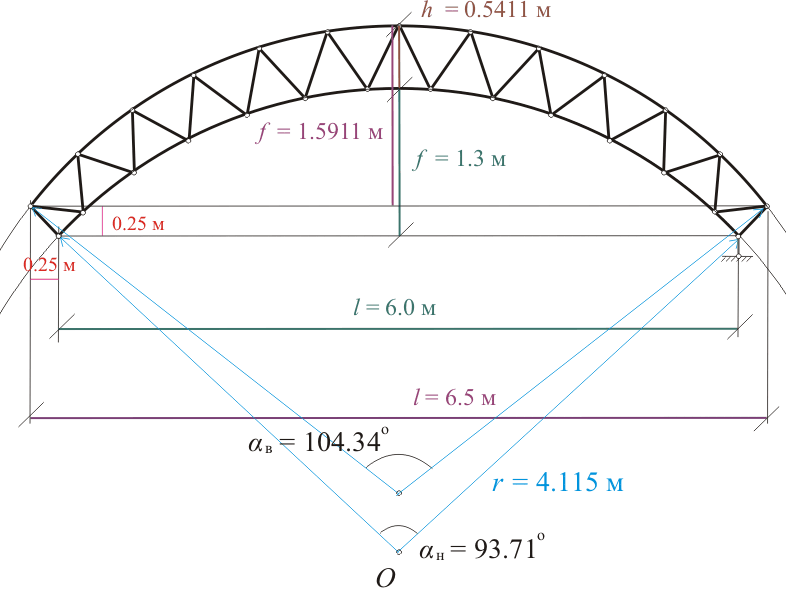
Рисунок 290.3. Принятая расчетная схема арочной фермы.
то на подобный расчет уйдет минимум времени, если принять стрелу арки равной f = 1.3 м и если для дополнительного упрощения расчета нагрузку от сотового поликарбоната и балок обрешетки условно рассматривать как равномерно распределенную, а снеговую нагрузку как квадратную параболу (расчетная схема 2.9)
Сосредоточенная нагрузка от собственного веса фермы, сотового поликарбоната и балок обрешетки у нас составляла Q = 19.72 кг (кроме крайних узлов, где нагрузка в 2 раза меньше). При пролете арки 6 м и 13 приложенных сосредоточенных нагрузок примем для расчета значение равномерно распределенной нагрузки от общего веса конструкции настила и от собственного веса балки
qк = 19.72·6·1·1.2/12 + 10 = 21.8 кг/м
где 1 - коэффициент перехода от сосредоточенной к распределенной нагрузке, в данном случае учитывающий не только количество балок обрешетки, но и разную длину пролетов в горизонтальной проекции арки. 1.2 - коэффициент запаса по прочности, 10 - ориентировочный вес арки из профильной трубы.
Максимальная снеговая нагрузка у нас составляла 180 кг/м, но это значение может не соответствовать квадратной параболе. При выбранной расчетной схеме основные расчетные значения реакций и нагрузок будут следующими
1. Вертикальные опорные реакции
Так как нагрузка на нашу симметричную арку является также симметричной при первом варианте снеговой нагрузки, то вертикальные опорные реакции будут такими же как и у фермы
VA = VB = qкl/2 + qsl/3 = 21.8·6/2 + qs·6/3 = 502.4 кгс
тогда расчетная снеговая нагрузка составит
qs = (502.4 - 65.4).2 = 218.5 кг/м
Максимальный изгибающий момент будет посредине бруса и составит
М = qкl2/8 + qsl2/9,6 = 21.8·62/8 + 218,5·62/9,6 = 917.5 кгм или 91750 кгсм
При расчетном сопротивлении стали Ry = 2350 кгс/см2 требуемый момент сопротивления:
Wтр = M/Ry = 91750/2350 = 39.04 см3
Этому требованию удовлетворяет труба 160х40х3 мм с моментом сопротивления W1 = 39.49 см3, площадью сечения F = 11.41 см2, масса погонного метра 8.96 кг.
Так как у нас максимальное расчетное значение снеговой нагрузки получилось значительно больше (218.5/180 = 1.21 раза), то попробуем определить значение изгибающего момента более точно (с учетом всех сосредоточенных сил, действующих в узлах фермы):
Мт = 3VA - 3.25Q1 - 2.8313Q2 - 2.3473Q3 - 1.8094Q4 - 1.23Q5 - 0.6221Q6 = 3·504.2 - 3.25·12.45 - 2.8313·36.89 - 2.3473·62.28 - 1.8094·88.19 - 1.23·111.21 - 0.6221·126 = 846.75 кгм или 84675 кгсм.
Впрочем профиль все равно потребуется такой же.
Такому моменту соответствует эквивалентная равномерно распределенная нагрузка
qэ = 8Мт/l2 = 8·846.75/62 = 188.17 кг/м
Это значение значительно облегчит нам дальнейшие расчеты.
Вот собственно и весь расчет по первому варианту. Кроме всего прочего он позволяет нам достаточно легко проверить, не ошиблись ли мы при достаточно сложных расчетах арочной фермы. Максимальное сжимающее усилие в стержне N8-м = 1559.51 кг.
При моменте М = 846.75 кгм и расстоянии между стержнями верхнего и нижнего пояса фермы h = 0.53 м значение сжимающего усилия в этом стержне составит:
N8-м(уп) = М/h = 846.75/0.53 = 1597.64 кгс
Это всего лишь на 2.5% больше точного значения.
Таким образом для предварительных, проверочных и упрощенных расчетов ферму вполне можно рассматривать как брус сквозного сечения.
Ну а мы продолжим расчеты.
2 вариант: Расчет криволинейного бруса - трехшарнирной арки
Самый простой способ рассчитать такую балку - воспользоваться расчетной схемой трехшарнирной арки. Напомню, такая расчетная схема предполагает наличие дополнительного - третьего шарнира в ключе арки.
Арка - такая хитрая конструкция, что изгибающие моменты в поперечных сечениях арки - минимальны, а если форма арки - парабола и нагрузка равномерно распределенная по всей длине арки, то моменты во всех сечениях равны нулю. Материал арки работает в основном на сжатие, потому использование расчетной схемы трехшарнирной арки для нашей арки, описываемой уравнением окружности, вполне допустимо. А если арка будет изготавливаться из двух труб, сваренных посредине, то такая расчетная схема допустима тем более. При такой расчетной схеме значение изгибающего момента в ключе арки будет равно 0. Трехшарнирная арка отличается от простого криволинейного бруса тем, что в арке появляются
2. Горизонтальные опорные реакции
Так как на арку действует только вертикальная нагрузка (ветровую нагрузку по ряду причин мы не учитываем), то горизонтальные опорные реакции будут равны по значению и противоположно направлены, а для определения одной из горизонтальных реакций достаточно составить уравнение моментов относительно дополнительно принятого нами шарнира - замка арки:
∑МС = VAl/2 - ql2/8 - HAf = 0 (294.1)
тогда
HA = Мт/f = 846.75/1.3 = 651.34 кгс (294.2)
где f - стрела арки, равная 1.3 м согласно рисунка 294.1.
3. Определение действующих напряжений в поперечных сечениях
Теперь следует определить максимальные внутренние напряжения в поперечных сечениях арочной балки. Для этого обычно строятся эпюры поперечных сил, изгибающих моментов и продольных усилий. Однако в данном случае проще определить указанные значения для трех характерных сечений - в начале арки, посредине - где замок и, например, в точке, расположенной посредине между началом арки и замком. Потому что, максимальная поперечная сила будет действовать в начале и конце арки, максимальная продольная сила - в замке арки, а максимальный момент примерно посередине пролетов между шарнирами.
В точке А:
Q = VAcos(a/2) + HAsin(a/2) = 502.4·0.6838 + 651.34·0.7296 = 818.76 кгс
M = 0
N = VAsin(a/2) + HA cos(a/2) = 502.4·0.7296 + 651.34·0.6838 = 811.93 кгс
В точке С (замок арки):
Q = Q7/2 = 65.4 кгс
М =0 (так как относительно этой точки мы и составляли уравнение моментов в при определении горизонтальной составляющей опорной реакции)
N = HA = 651.34 кгс
В точке D (середина между началом и замком арки):
Для этой точки следует знать координаты по осям х и у. И если с определением координаты по оси х больших проблем нет, так как х = l/4 = 6/4 = 1.5 м, то для определения координаты у нужно сначала определить стрелу арки с пролетом 3 м и тем же радиусом R = 4.115 м. Проще всего определить это значение графически:

Рисунок 294.1. Графическое определение стрелы арки с пролетом 3 м.
Тогда значение координаты у для точки D составит у = 1.3 - 0.3 = 1 м. А приблизительное значение угла наклона касательной к горизонтали составит β = arctg(0.6/1.5) = 21.8о.
Примечание: для более точного определения стрелы арки с пролетом 3 м нужно решить тригонометрическое уравнение (290.1.1).
Q = VAcosβ + HAsinβ - qэcosβх = 502.4·0.9284 + 651.34·0.3713 - 188.17·1.5·0.9284 = 446.2 кгс
М =VAx - HAy - qэx2/2 = 502.4·1.5 - 651.34·1 - 188.17·1.52/2 = - 109.43 кгс·м = - 10943 кгс·см
N = VAsinβ + HA cosβ - qэsinβх = 502.4·0.3717 + 651.34·0.9284 - 188.17·1.5·0.2535 = 719.9 кгс
Как видим, значение изгибающего момента в точке D относительно мало (в данном случае знак "-" означает, что растягивающие напряжения при действии изгибающего момента будут действовать в верхней части сечения арки), а максимальные внутренние напряжения будут возникать в начале и в конце арочной балки (в точках А и В).
4. Подбор сечения профильной трубы
В рассматриваемом нами поперечном сечении действует поперечная и продольная сила, а значит, возникают касательные и нормальные напряжения. Напомню, на сегодняшний день существует как минимум 5 теорий прочности и формулы, предлагаемые этими теориями для таких случаев несколько отличаются. Но мы пойдем как всегда по пути наибольшего запаса прочности и произведем расчет по третьей теории прочности согласно которой:
σпр = (σ2 +4т2)0.5 ≤ R = 2350 кгс/см2 (278.4), (278.5)
где σ - нормальное напряжение
σ = N/F
где F - площадь поперечного сечения профильной трубы
т - касательное напряжение
т = QSотс/bI
где Sотс = ∑уiFi - статический момент отсекаемой на рассчитываемой высоте части сечения, I - момент инерции сечения, b - ширина сечения на рассчитываемой высоте сечения.
Как видим, в уравнении (278.4) слишком много неизвестных и для решения такого уравнения проще использовать метод аппроксимации, проще говоря, подобрать требуемое сечение, исходя из имеющихся данных сортамента. Например, при расчете балок обрешетки для сотового поликарбоната мы подобрали квадратную профильную трубу сечением 30х30х3.5 мм. Для такой трубы площадь поперечного сечения F = 3.5 см2, момент сопротивления W = 2.65 см3, момент инерции I = 3.98 см4. Так как максимальные касательные напряжения будут на высоте, равной половине высоты сечения, то для такой трубы статический момент полусечения будет равен приблизительно
Sотс = 3·0.35(1.5 - 0.35/2) + 2(1.5 - 0.35)0.35(1.5 - 0.35)/2 = 1.854 см3
Тогда для сечения в точке А
σпр = ((914.82/3.5)2 + 4(919.1·1.854/((0.35 + 0.35)3.98)2)0.5 = 1250.96 < 2350 кг/см2
Для сечения в точке D
проверки на прочность не достаточно, арочную балку в этом сечении следует дополнительно проверить на устойчивость.
При радиусе инерции, равном i = 1.066 см, значение коэффициента гибкости составит
λ = μl/i = 0.6·673/1.066 = 379
Почему для трехшарнирной арки μ =0.6 и как определяется геометрическая длина арки, рассказывается отдельно. Такое значение коэффициента гибкости показывает, что арка, изготовленная из предварительно принятой нами трубы 30х30х3.5 мм, будет очень неустойчивой и для обеспечения устойчивости следует принять профиль большего сечения. Например, при использовании квадратной профильной трубы сечением 50х50х2 мм, имеющей площадь поперечного сечения F = 3.74 см2 (т.е. ненамного больше, чем площадь сечения профильной трубы 30х30х3.5 мм), момент сопротивления W = 5.66 см3, момент инерции I = 14.14 см4, радиус инерции i = 1.95 см, значение коэффициента гибкости составит 403.8/1.95 = 207
тогда по таблице 2 коэффициент изгиба φ = 0.16 (для стали С235 прочностью Ry = 2350 кгс/см2, определяется интерполяцией значений 2050 и 2450, а также интерполяцией значений 200 и 210)
Максимальные нормальные напряжения будут возникать в самом верху и самом низу поперечного сечения, т.е. в таких местах, где касательные напряжения стремятся к нулю, тогда
σпр = 719.9/(0.16·3.74) + 10943/5.66 = 1203.03 +1933.4 = 3136.4 > 2350 кгс/см2
Если использовать трубу сечением 50х50х3 мм с моментом сопротивления W2 = 7.78 см3 и площадью сечения F = 5.41 см2, то
σпр = 719.9/(0.155·5.41) + 10943/7.78 = 858.5 + 1406.5 = 2265 < 2350 кгс/см2
На высоте, равной половине высоты сечения, касательные напряжения будут максимальными, а вот значение изгибающего момента стремится к нулю и тогда при
Sотс = 5·0.3(2.5 - 0.3/2) + 2(2.5 - 0.3)0.3(2.5 - 0.3)/2 = 4.977 см3
σпр = (858.52 + 4(446.2·4.977/(0.6·19.45))2)0.5 = 939.1 < 2350 кг/см2
Как видим, выбранного сечения 50х50х3 мм вполне хватает для обеспечения прочности. Вот только значение гибкости λ = 212 является слишком большим для любого несущего элемента строительных конструкций. И хотя в СНиП II-23-81*(1990) "Стальные конструкции" предельно допустимая гибкость для стальных арок не указывается, но исходя из общих принципов, не должна превышать 150.
Таким образом, если рассматривать значение гибкости, как определяющий фактор, то сечение трубы нужно увеличивать, например до трубы 80х40х2 мм с радиусом инерции в интересующей нас плоскости i = 2.87 см, площадью сечения F = 4.54 см2, моментом сопротивления W = 9.34 см3 и массой погонного метра 3.56 кг
А еще после сгибания трубы в поперечных сечениях будут действовать остаточные напряжения сжатия и растяжения. Впрочем тут все будет сильно зависеть от технологии изгибания трубы. Самый надежный способ, остаточные напряжения после которого минимальны - гнуть трубу после нагревания участков трубы до температуры размягчения стали (около 500-600о).
И еще одна маленькая, но очень важная деталь. Как мы уже определили, в местах крепления арки к ригелям и в конечном счете к колоннам будут действовать силы, направленные горизонтально, а именно горизонтальные опорные реакции. Эти силы будут создавать довольно значительный изгибающий момент, действующий на колонны. Т.е. для расчетного поперечного сечения колонны длиной около 3 м, представляющей собой консольную балку, значение изгибающего момента составит М = 651.34·300 = 195402 кг·см. Это очень большой для нашей конструкции момент и если даже на колонну не будет действовать больше никаких нагрузок, то момент сопротивления сечения колонны должен быть не менее Wтр = 195402/2350 = 83.14 cм3. Т.е. потребуются трубы сечением минимум 140х120х4.5 мм с моментом сопротивления W = 91.35 см3.
Чтобы не перекладывать эту нагрузку на колонны, достаточно сделать арку с затяжкой, т.е. с дополнительным стержнем между точками А и В, воспринимающим горизонтальную нагрузку. Такой стержень будет работать на растяжение, а потому сечение его подбирается, исходя из требований по гибкости для растянутых элементов.
Так, согласно таблицы 476.1 предельно допустимая гибкость для затяжки составляет λmax = 400. Так как отдельно затяжка в указанной таблице не упоминается, то можно рассматривать ее как "Прочие элементы связей" (п.5). Впрочем, если рассматривать всю конструкцию в комплексе (арки, затяжки обрешетка, колонны), то ее можно отнести и к структурной, т.е. многократно статически неопределимой, при соответствующем решении узлов сопряжения элементов. Тогда затяжку следует рассматривать согласно п.2 и с учетом возможных динамических нагрузок (например, временных нагрузок при монтаже) λmax = 350. Это значение мы и будем использовать для дальнейших расчетов.
При расчетной длине затяжки l = 600 см минимально допустимое значение радиуса инерции составит:
i = l/λ = 600/350 = 1.71 см.
Это означает, что сечение затяжки в данном случае можно подбирать, исходя из технологических и эстетических соображений, но в итоге экономия материала по сравнению с балкой - криволинейным брусом будет уже не такой ощутимой.
3 вариант: Расчет криволинейного бруса - двухшарнирной арки
Если арка будет изготавливаться из цельного профиля, то такую арку более правильно рассматривать как двухшарнирную, т.е. 1 раз статически неопределимую. Это означает, что значение горизонтальной опорной реакции, которое мы так легко определили при наличии третьего шарнира, в данном случае будет неизвестной величиной.
Определить теоретически это значение достаточно трудоемко, учитывая непрямолинейную геометрию арки. Поэтому проще воспользоваться эмпирическими формулами и таблицами, в частности предлагаемыми "Справочником проектировщика" под ред. А.А. Уманского. Подробности подобного расчета здесь не приводятся. Далее остановимся на упрощенном расчете, основанном на следующих предположениях:
1. Если к криволинейному брусу, рассчитанному при 1 варианте расчета, добавить горизонтальную опорную связь, то мы получим двухшарнирную арку с затяжкой, в которой горизонтальные опорные реакции условно равны нулю (исходя из этого мы и выполняли расчет).
2. Если балку, рассчитанную по 2 варианту, рассматривать как двухшарнирную, то в ней горизонтальные опорные реакции также будут равны нулю до достижения предела допустимой нагрузки.
3. После превышения предела допустимой нагрузки в ключе арки образуется пластический шарнир, арка становится трехшарнирной, появляются горизонтальные усилия.
4. Соотношение моментов сопротивления труб из второго и первого варианта позволяет определить, когда в затяжке арки или на горизонтальных опорах появятся соответствующие горизонтальные усилия:
n = 1 - W2/W1 = 1 - 7.78/39.49 = 1- 0.197 = 0.8 (294.3)
Т.е. арка, рассчитанная по второму варианту может выдержать как балка не более 19.7% от нагрузки балки, рассчитанной по первому варианту.
5. Горизонтальные опорные реакции двухшарнирной балки равны:
H2ш = nН3ш (294.4)
Исходя из этих предположений, мы можем достаточно быстро пересчитать значения напряжений в интересующих нас точках:
В точке А:
Q = VAcos(a/2) + nHAsin(a/2) = 502.4·0.6838 + 0.8·651.34·0.7296 = 723.7 кгс
M = 0
N = VAsin(a/2) + nHA cos(a/2) = 502.4·0.7296 + 0.8·651.34·0.6838 = 722.86 кгс
В точке С (замок арки):
Q = Q7/2 = 65.4 кгс
М = 3VA - 1.3nHA - q32/2 = 3·502.4 - 1.3·0.8·651.34 - 188.17·4.5 = - 16.95 кгсм
N = nHA = 521.07 кгс
В точке D (середина между началом и замком арки):
Q = VAcosβ + HAsinβ - qэcosβх = 502.4·0.9284 + 0.8·651.34·0.3713 - 188.17·1.5·0.9284 = 397.85 кгс
М =VAx - HAy - qэx2/2 = 502.4·1.5 - 0.8·651.34·1 - 188.17·1.52/2 = 20.84 кгс·м = 2084 кгс·см
N = VAsinβ + HA cosβ - qэsinβх = 502.4·0.3717 + 0.8·651.34·0.9284 - 188.17·1.5·0.2535 = 598.95 кгс
Как видим, при таком расчете значение момента в точке D значительно уменьшилось и даже без дополнительных расчетов понятно, что исходя из условий прочности, вполне можно принимать трубу сечением 50х50х2 мм.
Так как для двухшарнирной арки при принятой геометрии коэффициет µ будет немного меньше (µ = 0.56), то соответственно уменьшится расчетная длина арки (до 375.76 см) и требования по радиусу инерции (iтр = 375.76/150 = 2.5 см). Тогда из соображений устойчивости можно принять трубу 70х50х2 мм (впрочем, масса погонного метра при этом не изменится, а значит и экономии по материалам не будет). Тем не менее
Вывод: Двухшарнирная арка является более эффективной с точки зрения использования материала и при определенных условиях расчет арки, как двухшарнирной, позволяет значительно уменьшить сечение трубы.
Если хочется сделать арку с длиной по горизонтали 6.5 м и с расстоянием между опорами 6 м, соответствующую верхнему поясу арочной фермы, то такую арку можно рассчитывать, как бесконсольную, т.е. с длиной по горизонтали 6 м, потому как никакой особенной нагрузки на консоли не будет. Снег на поверхностях с уклоном ≥ 50о не задерживается.
Для обеспечения устойчивости из плоскости арки одних только балок обрешетки и покрытия из поликарбоната будет недостаточно, необходимо предусмотреть соответствующие диафрагмы жесткости.
Ну а мы вернемся к нашим колоннам.
Если затяжку не делать и принять из соображений устойчивости трубу сечением 80х40х2 мм, то горизонтальные опорные реакции составят:
Н = (1 - 9.34/39.49)651.34 = 0.763·497.3 кгс
соответственно и значение требуемого момента сопротивления для колонн уменьшится и составит
Wтр = 0.763·83.14 = 63.43 см3
т.е. для колонн можно принять трубу 120х80х6 мм с моментом сопротивления W = 67.64 см3, что в общем то даст относительно небольшую экономию материалов в данном случае.
Таким образом мы можем сделать еще один полезный вывод из всего вышеизложенного: чем больше материала мы потратим на арку, тем больше материала мы сэкономим на колоннах.
P.S. Я прекрасно понимаю, что человеку, впервые столкнувшемуся с расчетом строительных конструкций, разобраться в тонкостях и особенностях вышеизложенного материала бывает не просто, но тратить тысячи или даже десятки тысяч рублей на услуги проектной организации вы все равно не хотите. Что ж, я готов помочь. Больше подробностей смотрите в статье "Записаться на прием к доктору". | 
